Передаточная функция является одним из ключевых понятий в теории автоматического управления. Она описывает зависимость выходного сигнала системы от входного сигнала.
Найти передаточную функцию по логарифмической амплитудно-частотной характеристике (ЛАХ) можно с помощью простого алгоритма и специальной формулы. ЛАХ представляет собой график зависимости амплитуды выходного сигнала от частоты входного сигнала. Анализируя ЛАХ, можно определить, как система реагирует на различные частоты входного сигнала и сформулировать соответствующую передаточную функцию.
Для нахождения передаточной функции по ЛАХ необходимо отметить на графике ЛАХ точку с отношением амплитуды равным 0dB, это будет точка среза. Затем находим частоту среза, которая соответствует этой точке. После этого вводим найденное значение частоты среза в специальную формулу и получаем передаточную функцию.
Что такое передаточная функция

Передаточная функция является стандартным способом представления системы управления в виде математической модели. Она отражает, как система реагирует на различные воздействия и позволяет оценить поведение системы в различных условиях.
Передаточная функция обычно представляется в виде рациональной функции, в которой числитель и знаменатель представляют собой полиномы. Числитель содержит коэффициенты, которые определяют свойства системы, а знаменатель содержит характеристики системы, такие как ее устойчивость и степень апроксимации исходной модели.
Знание передаточной функции позволяет анализировать и проектировать системы управления, оптимизировать их работу и предвидеть поведение системы в различных ситуациях. Часто передаточная функция используется при проектировании регуляторов, фильтров и других элементов систем управления.
Определение и основные понятия
Передаточная функция обычно обозначается символом H(s) и обычно имеет вид дробно-рациональной функции, где числитель и знаменатель являются полиномами от переменной s, которая представляет собой комплексное число.
Передаточная функция может быть задана в виде таблицы или графика, чтобы показать изменение выходного сигнала при различных значениях входного сигнала.
Основными понятиями, связанными с передаточной функцией, являются нули и полюса. Нули являются значениями переменной s, при которых передаточная функция обращается в ноль. Полюса являются значениями переменной s, при которых знаменатель передаточной функции обращается в ноль.
Зная передаточную функцию системы, можно анализировать и управлять ею, прогнозировать ее поведение и оптимизировать ее параметры. Поэтому поиск и определение передаточной функции является важной задачей в системном анализе и управлении.
| Символ | Описание |
|---|---|
| H(s) | Передаточная функция системы |
| s | Комплексное число |
| Нули | Значения, при которых H(s) = 0 |
| Полюса | Значения, при которых знаменатель H(s) = 0 |
Зачем нужно знать передаточную функцию
Знание передаточной функции позволяет нам понять, каким образом система реагирует на различные входные сигналы. Она отображает зависимость выходного сигнала системы от входного, и может быть представлена в аналитическом виде или графически. Таким образом, имея передаточную функцию, мы можем предсказать, как будет вести себя система при определенных условиях, и спланировать оптимальные стратегии управления.
Поиск передаточной функции является неотъемлемой задачей при анализе и моделировании сигналов и систем. Она позволяет нам установить зависимость между входными и выходными сигналами, и определить параметры системы, такие как амплитудная и фазовая характеристики, устойчивость и быстродействие.
Знание передаточной функции имеет широкое применение в различных областях, таких как автоматическое регулирование, электроника, сигнальная обработка, робототехника и другие. Она является основой для разработки управляющих алгоритмов и систем, а также используется при проектировании и настройке оборудования.
В целом, знание передаточной функции дает нам возможность лучше понять и контролировать системы, улучшить их работу, повысить эффективность и надежность. Поэтому она является неотъемлемой частью теории управления и системной техники.
Применение в научных и инженерных расчетах

С помощью передаточной функции можно легко описать математическую модель системы и производить различные расчеты, такие как определение устойчивости системы, анализ ее динамики, синтез регуляторов и фильтров, а также предсказание поведения системы в условиях различных воздействий.
Научные исследователи и инженеры используют лапласово преобразование и передаточную функцию для моделирования и анализа различных физических, электрических и механических систем. Они позволяют получить аналитические результаты и проводить численные расчеты с высокой точностью.
Также передаточная функция находит применение в разработке фильтров, схем компенсации и стабилизации, систем управления движением и прочих систем, где требуется анализ и регулирование сигналов и потоков энергии.
Благодаря своей универсальности и эффективности, использование передаточной функции и лапласового преобразования в научных и инженерных расчетах позволяет существенно упростить задачи моделирования, анализа и управления различными системами, что делает их незаменимыми инструментами в современной науке и технике.
Простой способ нахождения передаточной функции
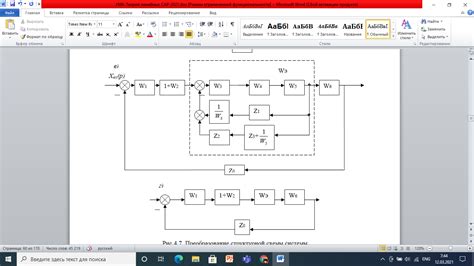
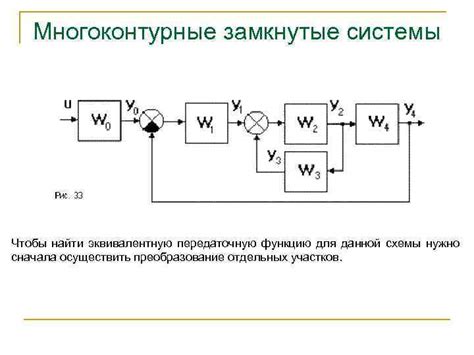
Для нахождения передаточной функции системы можно воспользоваться методом лаха. Этот метод позволяет установить связь между входными и выходными сигналами системы с использованием операторов и математических операций.
Один из простых способов нахождения передаточной функции состоит в следующих шагах:
- Запишите уравнение, описывающее систему в форме операционного идеала.
- Сделайте преобразование Лапласа обоих частей уравнения.
- Раскройте скобки, примените свойства преобразования Лапласа и упростите полученное выражение.
- Выразите передаточную функцию как отношение выходного и входного сигналов.
- Подставьте значения параметров системы в полученную формулу и получите конкретное значение передаточной функции.
Применение данного способа позволяет находить передаточную функцию системы с минимальными ошибками и без необходимости использования сложных математических выкладок.
Алгоритм и примеры вычислений
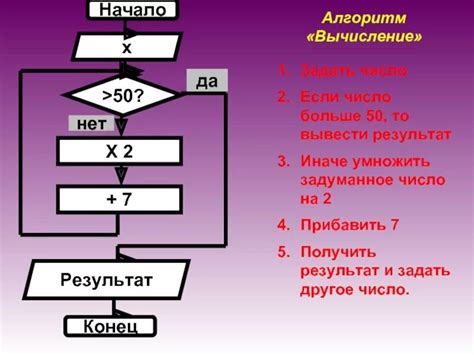
Для нахождения передаточной функции по лах следуйте следующему алгоритму:
- Соберите все необходимые данные для вычислений, включая значения входного и выходного сигналов, а также период дискретизации.
- Создайте лах-диаграмму, отображающую зависимость между входным и выходным сигналами.
- Рассчитайте разностное уравнение, выражающее отношение между входным и выходным сигналами.
- Примените преобразование Лапласа к разностному уравнению и найдите передаточную функцию.
- Проверьте полученную передаточную функцию на соответствие и контрольные вычисления.
Давайте рассмотрим пример вычислений:
Пусть у нас есть следующие данные:
- Входной сигнал: [1, 2, 3, 4]
- Выходной сигнал: [0, 1, 3, 6]
- Период дискретизации: 0.1 секунды
Используя эти данные, мы можем создать лах-диаграмму и рассчитать разностное уравнение.
После применения преобразования Лапласа к разностному уравнению, мы можем найти передаточную функцию:
G(s) = (1 - s) / (s^2)
Проверим нашу передаточную функцию, подставив значения входного сигнала:
G(1) = (1 - 1) / (1^2) = 0 / 1 = 0
Где G(1) - значение передаточной функции в точке s = 1.
Мы успешно нашли передаточную функцию по лах, используя данный пример вычислений.
Формула для определения передаточной функции

Для начала необходимо получить отношение преобразования входного сигнала к преобразованию выходного сигнала системы. Для этого рассмотрим два сигнала:
входной сигнал u(t) и выходной сигнал y(t). Соответственно, преобразованиями этих сигналов будут U(p) и Y(p). Применяя преобразования Лапласа к дифференциальным уравнениям, связывающим сигналы u(t) и y(t), мы получим следующую формулу:
H(p) = Y(p)/U(p)
Эта формула позволяет найти передаточную функцию H(p) по ЛАХ системы. После получения передаточной функции можно проводить анализ и проектирование системы управления, оптимизировать её параметры и улучшать её характеристики.
Для нахождения передаточной функции по лах существует простой способ и соответствующая формула. Основной шаг заключается в анализе системы и выявлении связей между входными и выходными сигналами.
Формула для нахождения передаточной функции по лах имеет следующий вид:
С(s) = Y(s) / X(s)
Где:
С(s) – передаточная функция
Y(s) – выходной сигнал в комплексной области частот (s)
X(s) – входной сигнал в комплексной области частот (s)
Важно отметить, что передаточная функция может быть представлена в различных формах, включая простые дроби, степенные ряды или матричные уравнения, в зависимости от сложности и типа системы.
Также необходимо учитывать, что нахождение передаточной функции по лах является одним из основных шагов при анализе и проектировании систем управления и обработки сигналов. Правильное определение передаточной функции позволяет смоделировать и предсказать поведение системы в различных условиях и оптимизировать ее параметры.
Важные аспекты при использовании передаточной функции

Выбор передаточной функции должен основываться на спецификации требований к системе и учете всех важных аспектов. Важно понимать, что передаточная функция является математическим приближением реальной системы, поэтому выбор правильной функции может оказать значительное влияние на точность и надежность анализа и управления системой.
Структура передаточной функции должна отражать физические принципы, лежащие в основе конкретной системы. Например, для электрической цепи может использоваться функция, включающая ёмкость, индуктивность и сопротивление, а для механической системы - функция, связывающая массу, силу и ускорение.
Анализ передаточной функции позволяет определить такие характеристики системы, как устойчивость, амплитудно-частотная и фазо-частотная характеристики, время переходного процесса, запасы устойчивости и др. Это позволяет оценить производительность системы и внести необходимые корректировки в процессе проектирования и эксплуатации системы.
Применение передаточной функции может быть полезным во многих областях, таких как автоматическое управление, электротехника, мехатроника и другие. Знание принципов работы и использования передаточной функции необходимо инженерам и специалистам в этих областях для эффективного проектирования и управления системами.
Особенности применения и практические советы

При использовании лапласовского преобразования для нахождения передаточной функции системы, полезно учитывать несколько особенностей и следовать некоторым практическим советам.
- Важно учесть, что лапласовское преобразование является инструментом для анализа динамических систем в частотной области. Поэтому, если система имеет нелинейные элементы или временные задержки, то применение лапласовского преобразования может быть ограничено.
- При анализе системы с использованием лапласовского преобразования, необходимо использовать правильные граничные условия, чтобы избежать ошибок и получить точные результаты.
- Важно понимать, что передаточная функция является математической моделью системы и может не полностью учитывать физические свойства реальной системы. Поэтому перед применением полученной передаточной функции в реальной системе следует провести дополнительные эксперименты и тесты.
- При нахождении передаточной функции по лапласовскому преобразованию, полезно использовать таблицы лапласовских преобразований, чтобы упростить вычисления и избежать ошибок.
- Необходимо помнить, что передаточная функция может иметь разные формы в зависимости от типа системы (непрерывная или дискретная) и типа входного сигнала (сигнал, импульс или ступенька).
Следуя указанным особенностям и советам, можно более эффективно и точно находить передаточные функции по лапласовскому преобразованию и использовать их в анализе и проектировании динамических систем.
Примеры использования передаточной функции
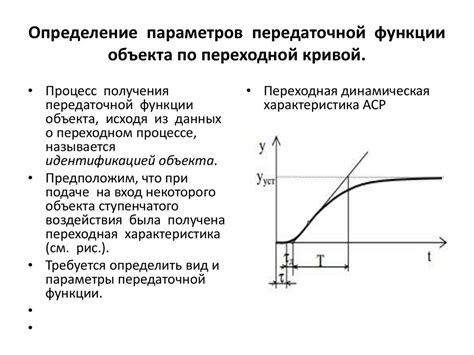
1. Анализ стабильности системы: Передаточная функция позволяет определить устойчивость системы управления. Если все корни характеристического уравнения, полученного из передаточной функции, расположены в левой полуплоскости комплексной плоскости, то система является устойчивой.
2. Определение переходных процессов: Передаточная функция позволяет описать поведение системы во временной области, а именно переходные процессы. На основе передаточной функции можно определить, как система будет реагировать на входной сигнал или изменения на входе.
3. Проектирование систем управления: Передаточная функция позволяет проектировать системы управления с нужными параметрами. Можно использовать передаточную функцию для определения коэффициентов регуляторов или фильтров, которые обеспечат требуемые характеристики системы.
4. Анализ чувствительности: Передаточная функция позволяет определить, как изменения параметров системы или входного сигнала влияют на выходной сигнал. Это позволяет оценить чувствительность системы к различным факторам и произвести соответствующие корректировки.
Передаточная функция является удобным инструментом для анализа и проектирования систем управления. Важно знать, как правильно использовать ее и правильно интерпретировать полученные результаты.