Периметр четырехугольника является одной из важнейших характеристик этой геометрической фигуры. Но что делать, если изначально известны только диагонали? В данной статье мы рассмотрим, как с помощью известных диагоналей найти периметр четырехугольника и разберем несколько примеров для более наглядного понимания.
Для начала, давайте разберемся, что такое периметр и что представляют собой диагонали четырехугольника. Периметр - это сумма всех сторон фигуры. Диагональ - это линия, соединяющая две несоседние вершины. У четырехугольника, в отличие от треугольника, есть две диагонали: главная диагональ (наибольшая) и побочная диагональ (наименьшая).
Чтобы найти периметр четырехугольника с известными диагоналями, необходимо использовать формулу, основанную на связи между диагоналями и сторонами четырехугольника. В случае, когда известны главная и побочная диагонали, можно воспользоваться следующей формулой: периметр равен сумме длин сторон плюс удвоенная длина главной диагонали плюс удвоенная длина побочной диагонали.
Четырехугольник с диагоналями: определение и особенности
Особенностью четырехугольников с диагоналями является то, что они могут быть различных типов в зависимости от свойств их сторон и углов. Например, если все стороны и углы четырехугольника равны, то он является ромбом. Если две стороны и два угла параллельны, то это параллелограмм.
Для определения периметра четырехугольника с известными диагоналями нужно знать значения диагоналей и других сторон, если они известны. Периметр четырехугольника - это сумма длин всех его сторон.
Если известны длины диагоналей и угол между ними, то можно использовать теорему косинусов для нахождения длин сторон четырехугольника. Затем, найдя все длины сторон, можно просто сложить их, чтобы получить периметр.
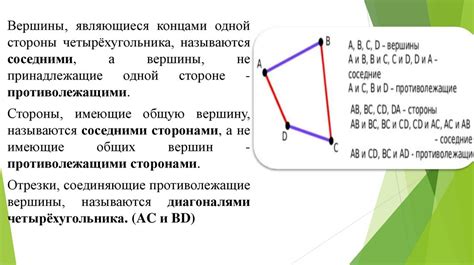
Например, если у нас есть четырехугольник ABCD, где AC и BD - диагонали, а AB, BC, CD и DA - стороны, то мы можем найти периметр, если знаем значения всех этих длин.
| Название | Длина |
|---|---|
| AB | 5 |
| BC | 6 |
| CD | 4 |
| DA | 7 |
| AC | 8 |
| BD | 9 |
Периметр четырехугольника ABCD будет равен сумме длин всех его сторон: P = AB + BC + CD + DA = 5 + 6 + 4 + 7 = 22.
Таким образом, периметр четырехугольника с известными диагоналями можно найти, зная значения диагоналей и сторон с помощью доступных формул и методов геометрии.
Что такое четырехугольник с известными диагоналями?
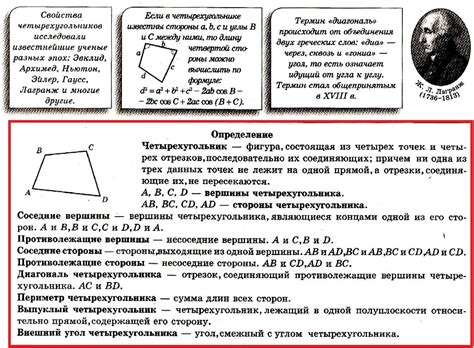
Известные диагонали могут быть полезны для нахождения других параметров четырехугольника, например, его периметра. Для этого часто используется теорема о четырехугольниках с известными диагоналями.
Как найти периметр четырехугольника с известными диагоналями?
Для начала, давайте определимся с тем, что такое диагональ четырехугольника. Диагональ - это отрезок, соединяющий две несоседние вершины четырехугольника.
Если у нас есть известные диагонали четырехугольника, мы можем использовать теорему Пифагора для нахождения длин его сторон. Для этого нужно разделить четырехугольник на два треугольника с одной из диагоналей в качестве основания.
Затем, мы сможем использовать теорему Пифагора для каждого из треугольников, чтобы найти длины всех четырех сторон четырехугольника. После этого, просто сложите все длины сторон, чтобы получить периметр.
Важно отметить, что в некоторых случаях могут быть даны не все диагонали четырехугольника. В таких случаях, нам нужно будет использовать другие методы для нахождения периметра.
Вот пример задачи:
- У нас есть четырехугольник ABCD с данными диагоналями AC и BD.
- Длина диагонали AC = 10 единиц.
- Длина диагонали BD = 12 единиц.
- Мы должны найти периметр четырехугольника ABCD.
Чтобы найти периметр, разделим четырехугольник на два треугольника с диагоналями AC и BD в качестве основания. После этого, используем теорему Пифагора для нахождения длин сторон каждого треугольника.
Для треугольника ABC:
- Длина стороны AB = √(AC² - BC²) = √(10² - BC²).
- Для треугольника BCD:
- Длина стороны BC = √(BD² - CD²) = √(12² - CD²).
После нахождения длин всех сторон четырехугольника, просто сложим их, чтобы получить периметр.
В этом примере, мы использовали теорему Пифагора для нахождения длин сторон четырехугольника ABCD. Если у вас есть данные о других сторонах или углах четырехугольника, может потребоваться использование других методов для нахождения его периметра. Важно помнить, что все данные должны быть правильно подведены к задаче.
Шаги для вычисления периметра

Для вычисления периметра четырехугольника с известными диагоналями необходимо выполнить следующие шаги:
- Определите значения диагоналей четырехугольника.
- Разбейте четырехугольник на два треугольника, соединяющиеся общей диагональю.
- Вычислите периметр каждого треугольника с помощью формулы P = a + b + c, где a, b и c - стороны треугольника.
- Сложите периметры двух треугольников, чтобы получить общий периметр четырехугольника.
Например, если диагонали четырехугольника равны 6 и 8, то, разбив четырехугольник на два треугольника, мы получим треугольники со сторонами 6, 8 и 10. Периметр каждого треугольника будет равен 24, а общий периметр четырехугольника - 48.
Пример вычисления периметра
Допустим, у нас есть четырехугольник ABCD, у которого известны две диагонали: AC и BD. Чтобы найти периметр этого четырехугольника, мы можем использовать формулу, которая связывает длины диагоналей с длинами сторон четырехугольника.
Давайте обозначим длину диагонали AC как d1 и длину диагонали BD как d2. Тогда формула для вычисления периметра P будет:
P = 2 * (d1 + d2)
Это связано с тем, что четырехугольник ABCD можно разделить на четыре треугольника: ABC, ABD, BCD и CDA. Каждый из этих треугольников является треугольником со сторонами, равными соответствующим сторонам четырехугольника, и диагоналями, равными диагоналям четырехугольника. Периметр каждого треугольника равен сумме его сторон, а так как каждая сторона треугольника является стороной четырехугольника, то для каждого треугольника периметр будет равен половине суммы длин диагоналей.
Теперь рассмотрим конкретный пример. Пусть диагональ AC равна 10 сантиметров, а диагональ BD равна 8 сантиметров. Тогда периметр четырехугольника ABCD будет:
P = 2 * (10 + 8) = 36 сантиметров
Таким образом, периметр четырехугольника ABCD равен 36 сантиметров.
Формула для расчета периметра

Для расчета периметра четырехугольника с известными диагоналями существует специальная формула:
| Периметр четырехугольника | = | AB | + | BC | + | CD | + | DA |
где AB, BC, CD и DA - длины сторон четырехугольника, соответственно. Обратите внимание, что в этой формуле используются только стороны четырехугольника, а не диагонали.
Например, если известны длины сторон четырехугольника AB = 5, BC = 7, CD = 3 и DA = 4, то периметр можно вычислить следующим образом:
| Периметр четырехугольника | = | 5 | + | 7 | + | 3 | + | 4 | = | 19 |
Таким образом, периметр четырехугольника с длинами сторон 5, 7, 3 и 4 равен 19.
Четырехугольник с известными диагоналями: примеры из реальной жизни
Периметр четырехугольника с известными диагоналями может быть вычислен с помощью формулы, которая учитывает длины диагоналей и углы между ними. Этот подход широко используется в различных областях, включая геометрию, инженерию и архитектуру.
Например, в строительстве четырехугольники с известными диагоналями широко применяются при планировке и измерении земельных участков. Зная длины диагоналей, можно определить периметр участка и корректно разместить на нем здания и строения.
В архитектуре четырехугольники с известными диагоналями используются для проектирования фасадов зданий. Зная диагонали оконных и фасадных элементов, архитекторы могут создавать гармоничные и пропорциональные композиции, которые визуально удлиняют или сокращают фасады зданий.
Также в геометрии четырехугольники с известными диагоналями часто встречаются при решении задач о расчете площади фигур. Зная длины диагоналей, можно вычислить площадь четырехугольника с помощью формулы Герона, которая основывается на полупериметре и длинах сторон.
Таким образом, четырехугольники с известными диагоналями имеют широкое применение в практических задачах и важны для различных областей знания, где требуется точный расчет периметра, площади или характеристик фигур.