Периметр фигуры - это сумма длин всех ее сторон. В математике нахождение периметра является одной из основных операций, которая позволяет определить длину границы фигуры. Знание правил и формул для вычисления периметра позволяет решать различные задачи, связанные с измерением длин линий или ограничений объекта.
Периметр является важной характеристикой геометрических фигур и часто используется для определения их размеров или сравнения. Например, периметр может указывать на длину ограждения участка земли или длину дороги, которую нужно пройти. Также, периметр может быть использован для определения длины провода, необходимого для обвязки объекта или объема материала, необходимого для изготовления изделия.
Вычисление периметра различных фигур имеет свои особенности и использует разные формулы. Например, периметр прямоугольника вычисляется по формуле: P = 2 * (a + b), где а и b - длины сторон прямоугольника. Для квадрата формула будет такой же, P = 4 * a, где а - длина стороны квадрата.
Периметр фигуры: как его найти, правила и формулы вычислений
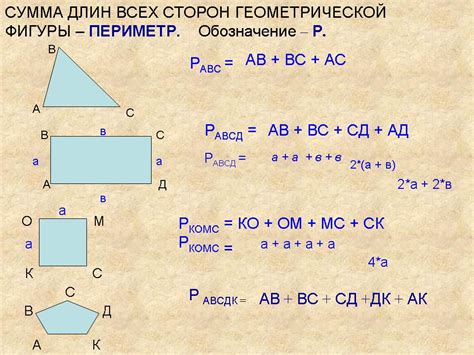
Для разных фигур существуют разные правила и формулы для вычисления периметра. Рассмотрим некоторые из них:
1. Прямоугольник:
Периметр прямоугольника можно вычислить по формуле:
P = 2 * (a + b),
где a и b - длины сторон прямоугольника.
2. Квадрат:
Периметр квадрата можно вычислить, зная длину одной его стороны:
P = 4 * a,
где a - длина стороны квадрата.
3. Круг:
Периметр круга называется длиной окружности. Он вычисляется по формуле:
P = 2 * π * r,
где π - математическая константа, равная приблизительно 3,14, r - радиус круга.
Знание правил и формул для вычисления периметра фигуры помогает решать разнообразные задачи по геометрии. Это особенно полезно при проектировании зданий, планировании участков и решении ежедневных математических задач.
Помните, что у каждой фигуры свои характеристики и формулы, поэтому важно правильно определить тип фигуры, чтобы правильно вычислить ее периметр.
Что такое периметр фигуры и его значение
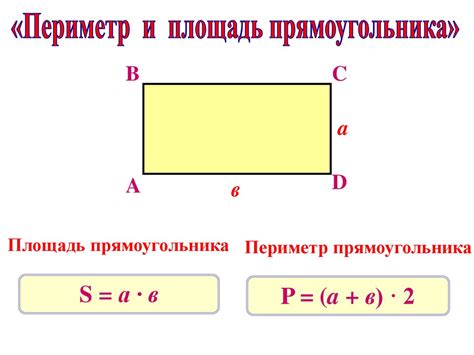
Значение периметра фигуры имеет важное значение при решении различных задач в геометрии и арифметике. Он позволяет определить, например, необходимую длину проволоки для ограждения участка или количество материала для строительства. Также периметр фигуры играет важную роль при вычислении длины пути или окружности.
Вычисление периметра фигуры зависит от ее формы и количества сторон. Для разных фигур существуют различные формулы для определения периметра. Например, для прямоугольника периметр равен удвоенной сумме длины и ширины, а для круга – удвоенному значению числа Пи, умноженному на радиус.
Имея значения длин сторон или радиус фигуры, возможно точно посчитать ее периметр и использовать эту информацию в практических расчетах и задачах.
Примеры:
| Фигура | Формула периметра |
|---|---|
| Прямоугольник | Периметр = 2*(длина + ширина) |
| Квадрат | Периметр = 4 * сторона |
| Круг | Периметр = 2 * π * радиус |
Зная формулу периметра и значения соответствующих параметров фигуры, вы всегда сможете точно определить значение периметра и использовать его в разнообразных задачах.
Периметр прямоугольника: как вычислить размеры
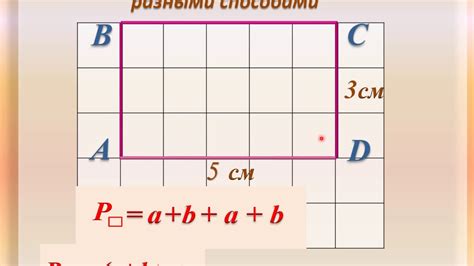
Для простоты обозначений, допустим, что длина прямоугольника равна a, а ширина равна b. Тогда формула для вычисления периметра будет следующей:
Периметр = 2a + 2b
Другими словами, чтобы найти периметр прямоугольника, нужно умножить длину одной стороны на 2, умножить ширину на 2, а затем сложить полученные значения.
Например, если длина прямоугольника равна 5 см, а ширина равна 3 см, то периметр будет равен:
Периметр = 2 * 5 см + 2 * 3 см = 10 см + 6 см = 16 см
Таким образом, периметр прямоугольника со сторонами 5 см и 3 см равен 16 см.
Вычисление периметра прямоугольника является простым и полезным математическим навыком, который может быть применен во многих ситуациях, связанных с измерением и построением различных фигур.
Периметр квадрата: формула для быстрого расчета

Для вычисления периметра квадрата достаточно умножить длину одной его стороны на 4. То есть, если длина стороны квадрата равна a, то периметр можно вычислить по формуле:
Периметр = a + a + a + a = 4a
Так как все стороны квадрата равны, нет необходимости знать значение каждой стороны отдельно. Достаточно знать только длину одной стороны и умножить ее на 4.
К примеру, если сторона квадрата равна 5 см, то периметр будет равен:
Периметр = 5 см + 5 см + 5 см + 5 см = 20 см
Итак, для быстрого расчета периметра квадрата необходимо знать только длину одной его стороны и умножить ее на 4. Теперь это правило не составит труда применить в практике!
Периметр треугольника: как определить его длину

Существует несколько способов вычисления периметра треугольника, в зависимости от доступной информации о его сторонах:
- Если известны длины всех трех сторон треугольника, то периметр можно получить суммированием этих значений. Например, если стороны треугольника равны 5, 7 и 9, то периметр будет равен 5 + 7 + 9 = 21.
- Если известны длины двух сторон треугольника и угол между ними, можно использовать теорему косинусов для вычисления длины третьей стороны. Затем периметр можно определить с помощью суммирования длин всех трех сторон.
- Если известны длины всех трех сторон треугольника, но необходимо определить его периметр с учетом координат точек, можно воспользоваться формулой геометрической длины отрезка, чтобы вычислить длины отрезков между точками.
Зная формулы и правила для вычисления периметра треугольника, можно легко определить его длину в различных ситуациях. Это поможет в решении задач из геометрии и архитектуры, а также при работе с фигурами в повседневной жизни.
Периметр круга: способы его вычисления
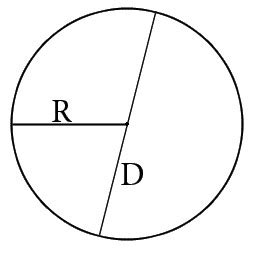
1. Длина окружности. Самым распространенным способом является вычисление периметра круга по формуле: П = 2пR, где П - периметр, п - число пи, R - радиус круга.
2. Длина диаметра. Периметр круга также можно вычислить, зная длину диаметра. Формула для этого выглядит следующим образом: П = пd, где П - периметр, п - число пи, d - длина диаметра.
3. Радиус и площадь. При известной площади круга можно вычислить его периметр по формуле: П = 2п √(S/п), где П - периметр, п - число пи, S - площадь круга.
4. Использование дуги. Если известна длина дуги окружности, можно вычислить периметр круга по следующей формуле: П = (длина дуги / угол) * 2п, где П - периметр, угол - угол, опирающийся на дугу окружности.
Важно помнить, что число пи (п) является иррациональным числом и приближенное значение 3,14 часто используется для простоты вычислений. Однако, для точных расчетов необходимо использование большего количества знаков.
Периметр остальных многоугольников: как справиться с задачами

Помимо прямоугольников и квадратов, существует множество других многоугольников, у которых также можно вычислить периметр. Зная правила и формулы для выполнения этих вычислений, можно решать разнообразные задачи, связанные с нахождением периметра многоугольников.
Один из таких многоугольников - треугольник. Для вычисления его периметра необходимо сложить длины всех его сторон. Если заданы значения длин сторон, то это делается достаточно просто. Если же известны координаты вершин треугольника, то для нахождения длин сторон можно использовать формулу расстояния между двумя точками в декартовой системе координат.
Если у нас задан выпуклый многоугольник с большим числом сторон, можно использовать следующий алгоритм:
- Пронумеруем вершины многоугольника в порядке обхода по часовой стрелке или против часовой стрелки.
- Найдем длину каждой стороны многоугольника, используя известные координаты вершин и формулу расстояния между двумя точками.
- Сложим все найденные длины сторон, чтобы получить периметр многоугольника.
Если многоугольник является невыпуклым, тогда процесс нахождения периметра может быть более сложным. В этом случае можно разделить невыпуклый многоугольник на несколько выпуклых многоугольников и найти периметр каждого из них по отдельности. Затем сложить найденные периметры, чтобы получить общий периметр исходного многоугольника.
Задачи на вычисление периметра многоугольников могут быть разными и требовать применения различных правил и формул. Поэтому важно освоить основные методы решения и практиковаться в их применении. С уверенностью в знании данных правил и формул, вы сможете успешно справиться с любыми задачами, связанными с нахождением периметра многоугольников.
Практический пример: вычисление периметра фигуры в реальной ситуации

Представьте себе, что вы занимаетесь озеленением двора в своем доме. Вы решили посадить круглый цветник в центре двора. Чтобы определить, сколько растений вам нужно купить, вам необходимо вычислить периметр этого цветника.
Периметр круга вычисляется по формуле:
P = 2πr
Где P - периметр, π (пи) - математическая константа, примерно равная 3.14, и r - радиус круга.
Для определения радиуса круга вам потребуется его диаметр. Пусть диаметр вашего цветника составляет 5 метров.
Теперь можно вычислить радиус:
r = диаметр / 2 = 5 / 2 = 2.5 метра
И, наконец, с помощью формулы находим периметр:
P = 2 * 3.14 * 2.5 ≈ 15.7 метра
Таким образом, вам понадобится приобрести растения на общую площадь примерно 15.7 метра, чтобы озеленить ваш круглый цветник.