Периметр – это сумма длин всех сторон фигуры. Знание формулы для нахождения периметра помогает решать задачи и измерять объекты вокруг нас. В данной статье мы рассмотрим основные формулы для вычисления периметра различных геометрических фигур и рассмотрим несколько примеров их применения.
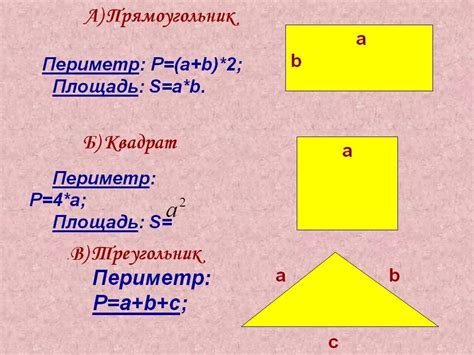
Периметр прямоугольника вычисляется по формуле: P = 2*a + 2*b, где a и b – длины сторон прямоугольника. Например, если стороны прямоугольника равны 5 см и 8 см, то периметр будет равен 2*5 + 2*8 = 10 + 16 = 26 см. Таким образом, периметр прямоугольника равен 26 см.
Периметр квадрата можно вычислить по формуле: P = 4*a, где a – длина стороны квадрата. Например, если сторона квадрата равна 6 см, то периметр будет равен 4*6 = 24 см.
Периметр треугольника может быть вычислен по формуле: P = a + b + c, где a, b и c – длины сторон треугольника. Например, если стороны треугольника равны 4 см, 7 см и 9 см, то периметр будет равен 4 + 7 + 9 = 20 см.
Что такое периметр и почему он важен?

Знание периметра позволяет нам решать различные задачи, связанные с пространственными объектами. Например, зная периметр, можно определить длину ограждения для сада или площади, которую нужно замостить. Периметр также помогает в расчетах, связанных с планировкой дома или построением забора.
Периметр также важен для повседневной жизни. Например, зная периметр своего телефона или планшета, можно подобрать чехол или защитную пленку, чтобы обеспечить защиту устройства.
В математике периметр играет важную роль в изучении геометрии, а также в решении различных задач. Он помогает определить форму и размеры фигуры, а также способствует развитию логического мышления и аналитических навыков. Поэтому понимание и умение вычислять периметр являются неотъемлемой частью математической грамотности.
Зачем нужно искать периметр?

В геометрии периметр используется для измерения длины сторон многоугольника, окружности, а также других сложных фигур. Это важно для расчета площади фигуры и для проверки ее соответствия требованиям проекта или задания. Например, при строительстве забора или прокладке дороги необходимо знать периметр участка, чтобы определить, сколько материала потребуется для ограждения или строительства.
В повседневной жизни рассчет периметра помогает определить длину тура или оградки дачного участка. Также с помощью периметра можно определить длину беговой дорожки, фитнес-трека или скользкой трассы. Зная периметр, можно выбрать необходимое количество материала для строительства ограждений, треков или дорожек.
Таким образом, расчет периметра является неотъемлемой частью геометрии и приложений в реальной жизни. Знание формулы для расчета периметра и практика его вычисления помогут вам в работе с различными фигурами и планировании проектов.
Как найти периметр прямоугольника?

Периметр прямоугольника = 2 * (длина + ширина)
Для примера, рассмотрим прямоугольник со сторонами 5 и 10:
- Найдем сумму длин сторон: 5 + 5 + 10 + 10 = 30.
- Удвоим полученную сумму: 30 * 2 = 60.
Таким образом, периметр прямоугольника со сторонами 5 и 10 равен 60.
Зная формулу для расчета периметра прямоугольника, вы можете легко найти периметр прямоугольника с любыми заданными длинами сторон.
Как найти периметр треугольника?
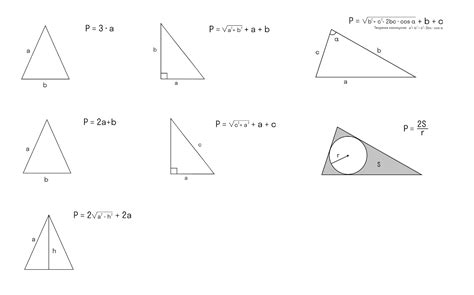
Если известны длины всех сторон треугольника, то периметр можно найти простым сложением этих длин:
Периметр треугольника (P) = длина первой стороны (a) + длина второй стороны (b) + длина третьей стороны (c)
Если же нам известны координаты вершин треугольника, то мы можем воспользоваться формулой расстояния между двумя точками в плоскости:
Пусть A(x1,y1), B(x2,y2) и C(x3,y3) – координаты вершин треугольника. Тогда периметр P можно найти по формуле:
Периметр треугольника (P) = √((x1 - x2)2 + (y1 - y2)2) + √((x2 - x3)2 + (y2 - y3)2) + √((x3 - x1)2 + (y3 - y1)2)
Таким образом, чтобы найти периметр треугольника, нужно либо знать длины его сторон, либо координаты его вершин.
Например, у нас есть треугольник со сторонами длиной 3, 4 и 5. В этом случае периметр будет:
Периметр треугольника (P) = 3 + 4 + 5 = 12
Теперь вы знаете, как найти периметр треугольника!
Формула периметра круга

Используя радиус (r) круга, формула для вычисления периметра (P) будет:
P = 2πr
Где π (пи) – это математическая константа, примерное значение которой равно 3.14.
Также, используя диаметр (d) круга, формула будет:
P = πd
То есть периметр круга можно вычислить, умножив диаметр на π или радиус на два и π.
Например, если радиус круга равен 5 см, то его периметр будет:
P = 2π * 5 см = 10π см
А если диаметр круга равен 10 см, его периметр будет:
P = π * 10 см = 10π см
Таким образом, формула периметра круга позволяет нам вычислить длину окружности и определить, насколько длинной будет граница круга.
Примеры поиска периметра
Для наглядного представления процесса нахождения периметра, рассмотрим несколько примеров.
Пример 1:
У нас есть прямоугольник со сторонами a = 4 см и b = 6 см. Чтобы найти периметр данного прямоугольника, нужно сложить длины всех его сторон:
Периметр = 2 * (a + b) = 2 * (4 см + 6 см) = 2 * 10 см = 20 см
Таким образом, периметр прямоугольника равен 20 см.
Пример 2:
Пусть у нас есть треугольник со сторонами a = 5 см, b = 7 см и c = 9 см. Чтобы найти периметр треугольника, необходимо сложить длины всех его сторон:
Периметр = a + b + c = 5 см + 7 см + 9 см = 21 см
Таким образом, периметр треугольника равен 21 см.
Пример 3:
Допустим, у нас есть круг с радиусом r = 3 см. Чтобы найти периметр круга, нужно воспользоваться формулой:
Периметр круга = 2 * π * r = 2 * 3.14 * 3 см ≈ 18.84 см
Таким образом, периметр круга примерно равен 18.84 см.
Это лишь несколько примеров расчета периметра различных геометрических фигур. Зная формулы и зная значения сторон или радиус, вы сможете без проблем найти периметр любой фигуры.