Понимание понятий площади и периметра является одним из важных элементов математической грамотности учащихся начальной школы. Ребенку важно научиться измерять и сравнивать длину сторон и площадь фигур, что поможет ему в решении различных задач.
Периметр - это длина замкнутой линии, ограничивающей фигуру. Для того чтобы найти периметр фигуры, нужно сложить длины всех ее сторон. Например, если у нас есть прямоугольник со сторонами 5 и 8 сантиметров, то его периметр будет равен 2*5 + 2*8 = 26 сантиметров.
Площадь - это мера внутренней поверхности фигуры. Для простых геометрических фигур существуют формулы для вычисления их площади. Например, для прямоугольника площадь вычисляется по формуле длина * ширина. Для нашего примера с прямоугольником площадь будет равна 5 * 8 = 40 квадратных сантиметров.
Важно дать ребенку возможность самостоятельно решать задачи по нахождению периметра и площади. Постепенно, с помощью практических заданий и игр, ученик сможет закрепить свои знания и навыки работы с площадью и периметром.
Как найти периметр и площадь
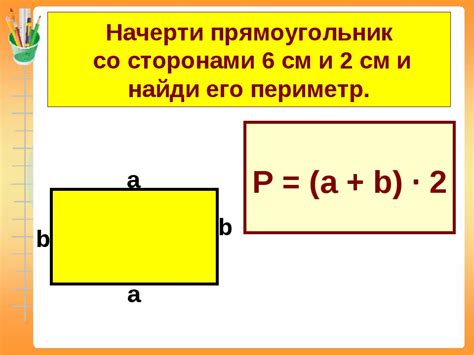
Периметр
Периметр – это сумма длин всех сторон фигуры. Для разных фигур существуют различные формулы для расчета периметра.
- Для прямоугольника периметр вычисляется по формуле: 2(а + b), где а и b - длины двух сторон прямоугольника.
- Для квадрата периметр также вычисляется по формуле: 4a, где a - длина стороны квадрата.
- Для треугольника периметр равен сумме длин всех трех его сторон: a + b + c, где a, b и c - длины сторон треугольника.
- Для окружности периметр называется длиной окружности и вычисляется по формуле: 2πr, где r - радиус окружности, а π - число Пи, примерно равное 3.14159.
Площадь
Площадь – это мера площади внутри геометрической фигуры. Для рассчета площади также используются различные формулы.
- Для прямоугольника площадь вычисляется по формуле: а * b, где а и b - длины двух сторон прямоугольника.
- Для квадрата площадь также вычисляется по формуле: a * a, где a - длина стороны квадрата.
- Для треугольника площадь можно найти по формуле Герона: √(p(p - a)(p - b)(p - c)), где a, b и c - длины сторон треугольника, а p - полупериметр треугольника, который вычисляется по формуле: (a + b + c) / 2.
- Для окружности площадь вычисляется по формуле: πr^2, где r - радиус окружности, а π - число Пи, примерно равное 3.14159.
Теперь, зная эти формулы, вы можете легко находить периметр и площадь различных геометрических фигур.
Определение периметра и площади
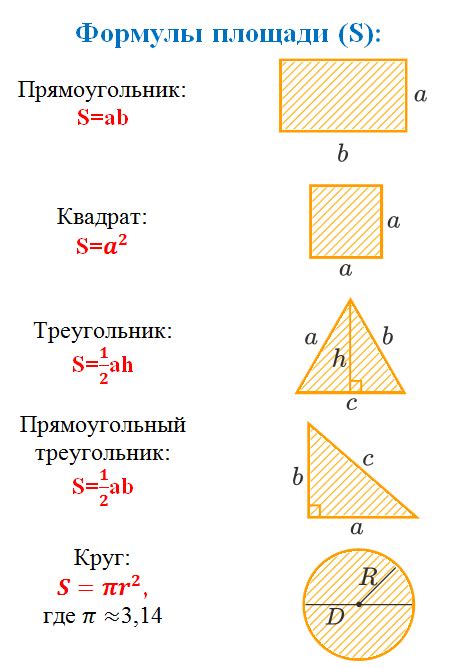
Периметр - это сумма длин всех сторон фигуры. Мы можем узнать, сколько длины нужно, чтобы обойти фигуру по ее границе.
Площадь - это количество пространства, занимаемое фигурой. Мы можем узнать, сколько площади занимает фигура, заполнив ее внутреннее пространство.
Для разных фигур существуют разные формулы для вычисления периметра и площади. Например, для прямоугольника периметр вычисляется по формуле: P = 2 * (a + b), где a и b - длины сторон прямоугольника. Площадь прямоугольника вычисляется по формуле: S = a * b.
Зная формулы, мы можем легко вычислить периметр и площадь разных фигур и использовать эти знания в повседневной жизни.
Формула для нахождения периметра

- Для прямоугольника периметр вычисляется по формуле: P = 2a + 2b, где a и b - длины сторон прямоугольника.
- Для квадрата периметр также вычисляется по формуле: P = 4a, где a - длина стороны квадрата.
- Для треугольника периметр равен сумме длин всех трех его сторон: P = a + b + c, где a, b и c - длины сторон треугольника.
- Для круга периметр называется длиной окружности и вычисляется по формуле: P = 2πr, где π - математическая постоянная, примерно равная 3.14159, и r - радиус окружности.
Знание формул для нахождения периметра поможет вам решать задачи с различными фигурами и определить их общую длину границы.
Примеры задач на нахождение периметра
Пример 1:
У прямоугольника длина одной стороны равна 4 см, а ширина - 6 см. Найдите периметр прямоугольника.
Решение:
Периметр прямоугольника можно найти, сложив длины всех его сторон. В данной задаче имеются две стороны: длина и ширина, поэтому нужно сложить два раза по 4 см и два раза по 6 см.
Периметр равен: 4 см + 4 см + 6 см + 6 см = 20 см.
Пример 2:
У треугольника две стороны равны 5 см, а третья сторона равна 7 см. Найдите периметр треугольника.
Решение:
Периметр треугольника можно найти, сложив длины всех его сторон. В данной задаче имеется три стороны: 5 см, 5 см и 7 см. Нужно их все сложить:
Периметр равен: 5 см + 5 см + 7 см = 17 см.
Пример 3:
У квадрата все стороны равны 9 см. Найдите периметр квадрата.
Решение:
Периметр квадрата можно найти, умножив длину одной стороны на 4 (так как у квадрата все стороны равны). В данном примере все стороны равны 9 см, поэтому периметр можно найти следующим образом:
Периметр равен: 9 см + 9 см + 9 см + 9 см = 36 см.
Формула для нахождения площади
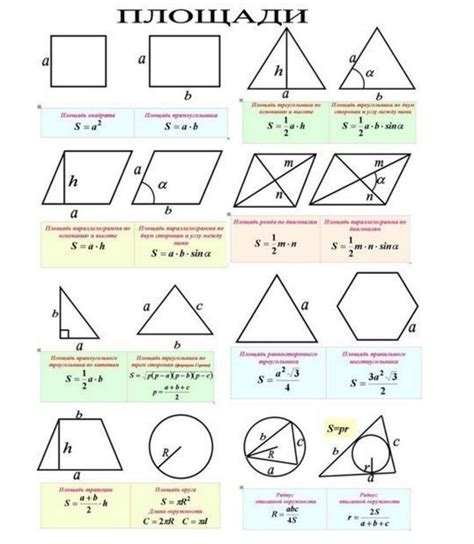
Если мы говорим о прямоугольнике, то его площадь можно вычислить с помощью формулы: S = a * b, где a и b – длины сторон прямоугольника.
Для квадрата формула будет такая же, как у прямоугольника: S = a * a, где a – длина стороны квадрата.
Для треугольника площадь можно найти с помощью формулы Герона: S = √(p * (p - a) * (p - b) * (p - c)), где p – полупериметр треугольника, а a, b и c – длины его сторон.
Для круга площадь можно вычислить по формуле: S = π * r * r, где π (pi) – математическая константа, приближенно равная 3,14, а r – радиус окружности.
Это лишь некоторые из формул для нахождения площади различных фигур. Зная эти формулы, вы сможете с легкостью вычислить площадь любой фигуры.
| Фигура | Формула для площади |
|---|---|
| Прямоугольник | S = a * b |
| Квадрат | S = a * a |
| Треугольник | S = √(p * (p - a) * (p - b) * (p - c)) |
| Круг | S = π * r * r |
Примеры задач на нахождение площади
Рассмотрим несколько примеров задач, в которых необходимо найти площадь различных фигур.
1. Найдите площадь прямоугольника, если его длина равна 5 см, а ширина - 3 см.
Решение: для нахождения площади прямоугольника необходимо умножить его длину на ширину. В данном случае, площадь равна 5 * 3 = 15 см².
2. Найдите площадь квадрата, если его сторона равна 9 см.
Решение: для нахождения площади квадрата необходимо возвести в квадрат длину его стороны. В данном случае, площадь равна 9² = 81 см².
3. Найдите площадь треугольника, если его основание равно 6 см, а высота - 4 см.
Решение: для нахождения площади треугольника необходимо умножить половину его основания на высоту. В данном случае, площадь равна 0.5 * 6 * 4 = 12 см².
4. Найдите площадь окружности, если её радиус равен 7 см.
Решение: для нахождения площади окружности необходимо возвести в квадрат радиус и умножить результат на число пи (π), которое примерно равно 3.14. В данном случае, площадь равна 3.14 * 7² = 3.14 * 49 = 153.86 см².
Таким образом, нахождение площади различных фигур требует знания соответствующих формул и применение элементарных математических операций.
| Фигура | Формула |
|---|---|
| Прямоугольник | Площадь = длина * ширина |
| Квадрат | Площадь = сторона * сторона |
| Треугольник | Площадь = 0.5 * основание * высота |
| Окружность | Площадь = π * радиус² |