Гипотенуза треугольника – это наибольшая сторона, она соединяет два угла прямоу
Как найти периметр и площадь гипотенузы треугольника: инструкция и формулы
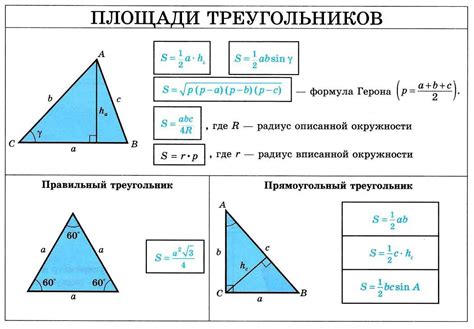
Формула для нахождения периметра треугольника: P = a + b + c, где P - периметр, а a, b и c - длины сторон треугольника.
Площадь треугольника - это мера его площади. Чтобы найти площадь треугольника, можно использовать формулу Герона или формулу основания и высоты.
Формула Герона для нахождения площади треугольника: S = √(p * (p - a) * (p - b) * (p - c)), где S - площадь, а p - полупериметр (p = (a + b + c) / 2).
Формула площади треугольника через высоту: S = (a * h) / 2, где S - площадь, a - основание треугольника, h - высота, опущенная на основание.
Гипотенузой треугольника называется его наибольшая сторона, которая является противоположной прямому углу.
Для нахождения гипотенузы прямоугольного треугольника можно использовать теорему Пифагора.
Теорема Пифагора: a^2 + b^2 = c^2, где c - гипотенуза, а a и b - катеты треугольника.
Используя формулы и инструкции, приведенные выше, вы с легкостью сможете найти периметр и площадь гипотенузы треугольника для решения математических задач и заданий.
Значение гипотенузы в треугольнике: определение и применение

Для нахождения периметра треугольника, необходимо сложить длины всех его сторон, включая гипотенузу. Поэтому знание значения гипотенузы позволяет точно определить периметр треугольника.
Также значение гипотенузы применяется для вычисления площади треугольника. Для прямоугольного треугольника с гипотенузой, длина которой равна c, и одной из его катетов, длина которого равна b, площадь можно вычислить по формуле:
S = (b*c)/2
Эта формула основана на свойстве прямоугольного треугольника, согласно которому площадь равна половине произведения длин катетов.
Важно отметить, что гипотенуза может быть доступна для вычислений только в прямоугольном треугольнике. В остальных случаях, где треугольник не является прямоугольным, значение гипотенузы может быть вычислено через теорему Пифагора, если длины двух других сторон известны.
Изучение значения гипотенузы в треугольнике позволяет решать задачи по вычислению его периметра и площади, что является важным навыком в геометрии и других областях, где треугольники играют роль.
Как найти периметр треугольника с гипотенузой: шаги и формулы расчета
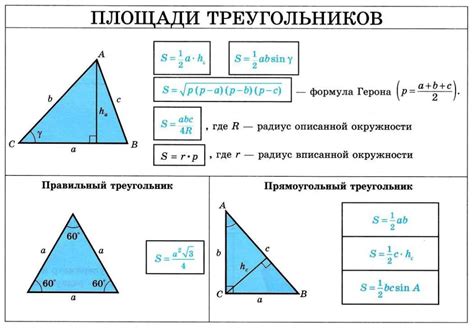
Шаги для нахождения периметра треугольника с гипотенузой:
- Определите значения длин основных сторон треугольника, кроме гипотенузы.
- Сложите длины всех сторон треугольника, чтобы получить периметр.
Формула для расчета периметра треугольника:
| Формула | |
|---|---|
| Периметр | периметр = длина стороны 1 + длина стороны 2 + длина стороны 3 |
Например, если длины сторон треугольника равны 5, 8 и 10, то:
Периметр = 5 + 8 + 10 = 23
Таким образом, периметр данного треугольника равен 23.
Используя указанные шаги и формулу, вы сможете легко вычислить периметр треугольника с известной гипотенузой.
Как найти площадь треугольника с гипотенузой: пошаговая инструкция и формулы
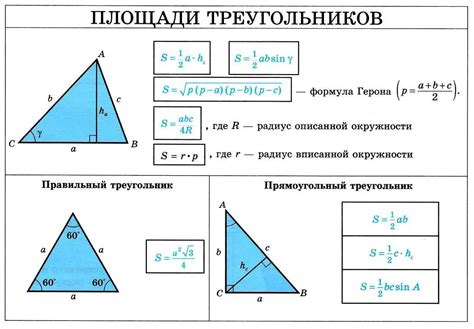
Чтобы найти площадь треугольника с гипотенузой, необходимо знать длины его сторон и использовать соответствующую формулу. Вот пошаговая инструкция:
- Определите длины сторон треугольника. В данном случае, гипотенуза уже известна, поэтому вам необходимо измерить или уточнить длины оставшихся двух сторон.
- Используйте формулу для нахождения площади треугольника. Формула для площади треугольника в общем виде выглядит следующим образом: S = (a * b) / 2, где S - площадь треугольника, а и b - длины двух сторон, не являющихся гипотенузой.
- Подставьте известные значения в формулу и выполните необходимые математические операции. Результат будет площадь треугольника с гипотенузой.
Например, если известно, что гипотенуза треугольника равна 7 единицам, а длины оставшихся сторон равны 4 и 5 единицам, то можно применить формулу: S = (4 * 5) / 2 = 10.
Теперь вы знаете, как найти площадь треугольника с гипотенузой, используя пошаговую инструкцию и соответствующую формулу.