Квадрат – это геометрическая фигура, которая имеет четыре одинаковые стороны и четыре прямых угла.
В 4 классе, при изучении геометрии, одной из основных задач является нахождение периметра и площади квадрата. Научиться выполнять эти простые расчеты поможет правильное понимание формул и примеров.
Периметр квадрата – сумма длин всех его сторон. Для нахождения периметра используется формула: P = 4 * a, где P – периметр квадрата, а a – длина одной стороны. Рассмотрим пример: если у нас есть квадрат со стороной длиной 5 см, то периметр будет равен 4 * 5 = 20 см.
Площадь квадрата – это площадь плоскостей внутри квадрата. Для нахождения площади используется формула: S = a * a, где S – площадь квадрата, а a – длина одной стороны. Например, если у нас есть квадрат со стороной длиной 3 см, то площадь будет равна 3 * 3 = 9 см².
Что такое периметр и площадь квадрата 4 класс

Площадь квадрата - это количество квадратных единиц, которыми можно полностью заполнить его внутреннюю площадь. Чтобы найти площадь квадрата, нужно возвести в квадрат длину его стороны.
Например, если сторона квадрата равна 5 см, то его периметр будет равен 20 см (5 + 5 + 5 + 5) и площадь будет равна 25 см² (5 * 5).
Зная периметр или площадь квадрата, можно решать задачи на вычисление длины стороны, если известен один из этих параметров.
Периметр и площадь квадрата важны для понимания геометрических понятий и решения различных задач, связанных с квадратами. Они помогают оценить размеры и свойства квадратов в повседневной жизни и могут быть полезными в различных областях знаний, таких как инженерия, архитектура и дизайн.
Определение понятий

Периметр = длина стороны × 4
Площадь квадрата - это площадь его внутренней поверхности. Площадь квадрата можно вычислить, зная длину одной из его сторон. Формула для нахождения площади квадрата следующая:
Площадь = длина стороны × длина стороны
Например, если у нас есть квадрат со стороной длиной 5 см, то его периметр будет равен 5 × 4 = 20 см, а площадь - 5 × 5 = 25 см².
Формулы для расчета периметра и площади квадрата
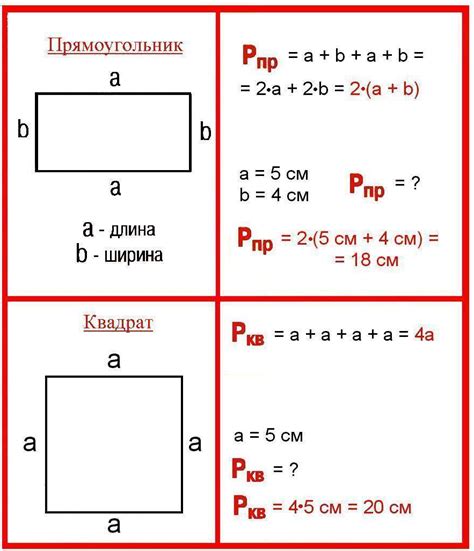
Периметр квадрата - это сумма длин всех его сторон. Так как у квадрата все стороны равны, то периметр можно найти, умножив длину одной стороны на 4:
П = 4 * a, где а - длина стороны квадрата.
Площадь квадрата - это площадь его внутренней поверхности. Площадь квадрата можно найти, возведя длину одной стороны в квадрат:
Площадь = а * а, где а - длина стороны квадрата.
Теперь, когда мы знаем формулы для расчета периметра и площади квадрата, мы можем приступить к решению различных задач и примеров, связанных с данными значениями. Не забывайте, что единицы измерения сторон квадрата должны быть одинаковыми для правильного расчета периметра и площади.
Как найти периметр квадрата 4 класс: примеры расчета

Для примера рассмотрим квадрат со стороной 5 см.
- Длина одной стороны квадрата: 5 см
- Периметр квадрата: 5 см x 4 = 20 см
Таким образом, периметр квадрата со стороной 5 см равен 20 см.
Еще один пример: рассмотрим квадрат со стороной 8 м.
- Длина одной стороны квадрата: 8 м
- Периметр квадрата: 8 м x 4 = 32 м
Таким образом, периметр квадрата со стороной 8 м равен 32 м.
Зная формулу для расчета периметра квадрата и имея значения длины его стороны, можно легко найти периметр любого квадрата.
Как найти площадь квадрата 4 класс: примеры расчета
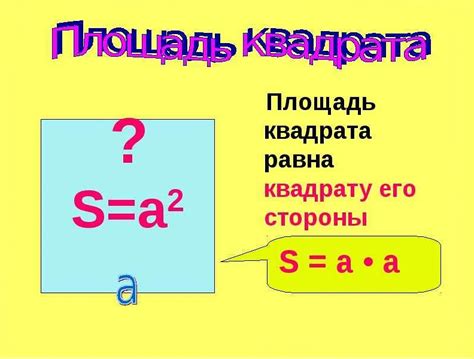
Для того чтобы найти площадь квадрата, нам необходимо знать длину его стороны. Площадь квадрата вычисляется по следующей формуле:
Площадь = длина стороны * длина стороны
Приведем несколько примеров расчета площади квадрата:
- Пример 1:
- Пример 2:
- Пример 3:
Допустим, у нас есть квадрат со стороной длиной 5 см.
Площадь = 5 см * 5 см = 25 см²
Представим, что сторона квадрата имеет длину 7 метров.
Площадь = 7 м * 7 м = 49 м²
Пусть у нас есть квадрат со стороной длиной 10 дециметров.
Площадь = 10 дм * 10 дм = 100 дм²
Таким образом, для нахождения площади квадрата нужно возведенить длину его стороны в квадрат.
Закономерности и свойства квадрата, связанные с периметром и площадью
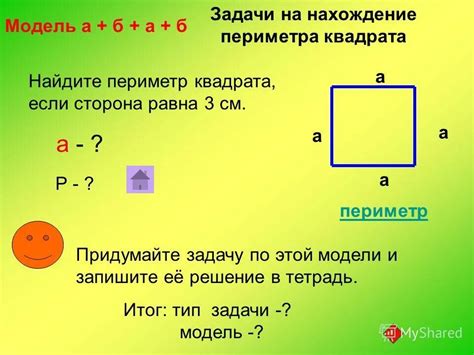
Периметр квадрата можно найти, складывая длины всех его сторон. Поскольку у квадрата все стороны равны, можно воспользоваться формулой:
Периметр = 4 × длина стороны квадрата.
Или можно просто умножить длину одной стороны на 4.
Площадь квадрата находится, умножая длину стороны на саму себя.
Площадь = длина стороны × длина стороны.
Так как все стороны квадрата равны, то можно сказать, что площадь равна стороне, возводимой в квадрат.
Знание этих формул и свойств поможет легко находить периметр и площадь квадратов. Попробуйте применить их на практике с помощью следующих примеров.
Разные единицы измерения периметра и площади
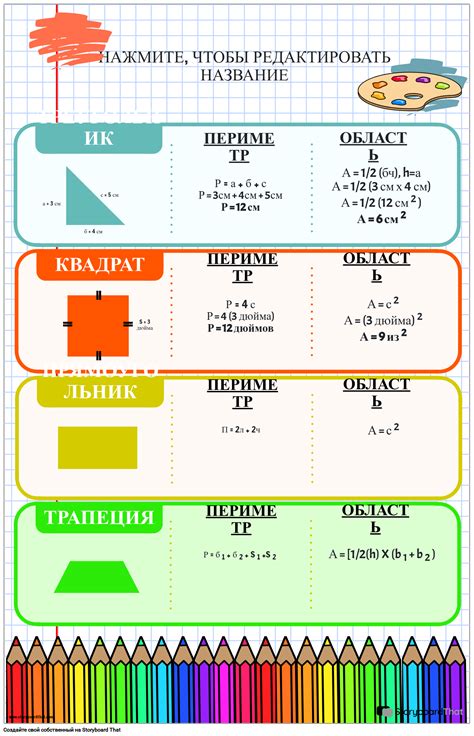
Когда мы рассчитываем периметр и площадь квадрата, обычно мы используем единицы измерения длины и площади. Самые распространенные единицы измерения периметра включают сантиметры (см) и метры (м). Например, если сторона квадрата равна 5 см, то периметр будет равен 5 см + 5 см + 5 см + 5 см = 20 см, а если сторона равна 3 метра, то периметр будет равен 3 м + 3 м + 3 м + 3 м = 12 м.
Единицы измерения площади часто также включают сантиметры квадратные (см²) и метры квадратные (м²). Например, если сторона квадрата равна 4 см, то площадь будет равна 4 см × 4 см = 16 см², а если сторона равна 2 метра, то площадь будет равна 2 м × 2 м = 4 м².
Важно помнить, что при работе с единицами измерения периметра и площади, необходимо использовать одинаковые единицы для всех сторон и размеров. Это помогает нам получить точные и понятные результаты и упрощает сравнение и анализ размеров.
Практические задания на расчет периметра и площади квадрата для 4 класса
Раздел, предлагаемый ниже, содержит ряд практических заданий, которые помогут вам закрепить материал о расчете периметра и площади квадрата.
Задание 1:
Найдите периметр и площадь квадрата, сторона которого равна 5 см.
Задание 2:
Рассчитайте периметр и площадь квадрата, если его сторона составляет 8 см.
Задание 3:
У вас есть квадрат со стороной 12 см. Определите его периметр и площадь.
Задание 4:
Найдите периметр и площадь квадрата, сторона которого равна 3 см.
Решите предложенные задания самостоятельно, используя формулы для расчета периметра и площади квадрата. Убедитесь, что вы правильно применяете эти формулы для каждого задания, а также проверьте свои ответы.