Периметр и площадь треугольника - это две основные характеристики этой геометрической фигуры. Зная значения сторон треугольника и его высоту, мы можем легко определить эти величины. Однако, что делать, если у нас есть два треугольника, которые являются подобными? В этой статье мы рассмотрим способы нахождения периметра и площади треугольников, которые имеют одинаковые формы, но различные размеры.
Периметр треугольника - это сумма длин его сторон. В подобных треугольниках соотношение между длинами соответствующих сторон одинаково. Это означает, что если мы знаем периметр и одну сторону одного треугольника, то мы можем найти периметр и стороны другого треугольника, используя пропорциональность.
Площадь треугольника - половина произведения длины основания на высоту. Для подобных треугольников соотношение между длинами сторон равно соотношению между площадями этих треугольников. Это позволяет нам использовать пропорциональность для нахождения площади в подобных треугольниках.
В этой статье мы рассмотрим несколько примеров и задач, чтобы полностью разобраться с формулами и алгоритмами нахождения периметра и площади в подобных треугольниках. Узнав эти методы, вы сможете с легкостью решать задачи, связанные с треугольниками, и применять их на практике во множестве ситуаций.
Что такое подобные треугольники и зачем нужно находить их периметр и площадь?

Подобными называются треугольники, у которых соответственные стороны пропорциональны, а соответствующие углы равны. Это означает, что два треугольника имеют одинаковую форму, но могут быть разных размеров.
Знание периметра и площади подобных треугольников имеет большую практическую значимость. Периметр треугольника - это сумма длин его сторон, а площадь - это площадь, ограниченная его сторонами. Нахождение периметра и площади позволяет определить характеристики треугольника, его размеры и свойства.
Кроме того, нахождение периметра и площади подобных треугольников позволяет решать множество задач в различных областях. Например, при планировании строительства, геодезии, архитектуре и дизайне это позволяет определить размеры и формы объектов. В математических расчетах и физических моделях периметр и площадь помогают понять особенности объектов, прогнозировать и проводить анализ.
Таким образом, нахождение периметра и площади подобных треугольников является неотъемлемой частью математического анализа и применяется в различных сферах человеческой деятельности.
Определение подобных треугольников
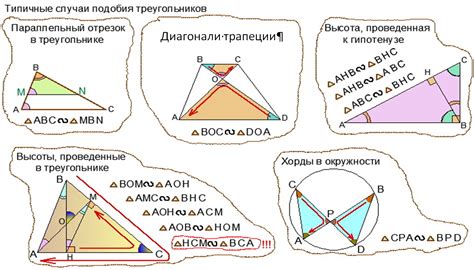
Два треугольника считаются подобными, если:
- Углы одного треугольника соответственно равны углам другого треугольника.
- Соответствующие стороны треугольников пропорциональны.
Символически это можно записать следующим образом:
Треугольник ABC подобен треугольнику DEF.
Пропорциональность сторон можно выразить при помощи отношения длин сторон двух подобных треугольников:
AB/DE = BC/EF = AC/DF
Знание о подобии треугольников позволяет применять соответствующие формулы для нахождения их периметра и площади.
Основные свойства подобных треугольников
1. Соотношение сторон: В подобных треугольниках отношение длин сторон одного треугольника к длинам соответствующих сторон другого треугольника всегда одинаково. Это соотношение называется коэффициентом подобия и обозначается буквой k. Таким образом, если стороны первого треугольника обозначены a, b, c, а стороны второго треугольника - x, y, z, то верно следующее соотношение:
| Первый треугольник | Второй треугольник |
|---|---|
| a : x = b : y = c : z |
2. Соотношение площадей: Площади подобных треугольников связаны соотношением, равным квадрату коэффициента подобия. Если площадь первого треугольника равна S, а площадь второго треугольника - S', то верно следующее соотношение:
S' = k² * S
3. Соотношение периметров: Периметры подобных треугольников связаны соотношением, равным коэффициенту подобия. Если периметр первого треугольника равен P, а периметр второго треугольника - P', то верно следующее соотношение:
P' = k * P
4. Соотношение высот и медиан: В подобных треугольниках соотношение высот и медиан, проведенных из соответствующих углов, также равно коэффициенту подобия.
Зная указанные свойства, можно применять их для нахождения периметра, площади и других параметров подобных треугольников.
Как найти коэффициент подобия между двумя треугольниками?

Коэффициент подобия между двумя треугольниками можно найти, сравнивая соответствующие стороны и углы в обоих треугольниках. Когда два треугольника подобны, их соответствующие стороны пропорциональны, а соответствующие углы равны.
Для того чтобы найти коэффициент подобия между двумя треугольниками, можно воспользоваться формулой:
коэффициент подобия = длина стороны второго треугольника / длина соответствующей стороны первого треугольника
Если известно, что два треугольника подобны, но не известны их стороны, можно использовать соотношение между их площадями или периметрами. Найдите отношение площадей двух треугольников или периметров и возведите его в квадрат, чтобы получить коэффициент подобия.
Например, если отношение площадей двух треугольников равно 4, то коэффициент подобия будет равен √4 = 2.
Используя найденные коэффициенты подобия, вы можете определить соответствующие стороны и углы второго треугольника, зная их значения в первом треугольнике.
Формула для нахождения периметра подобных треугольников
Когда речь идет о подобных треугольниках, их стороны пропорциональны друг другу. Используя эту свойство подобия, можно вывести формулу для нахождения периметра подобных треугольников.
Для двух подобных треугольников соотношение между длинами их сторон равно соотношению длин соответствующих сторон. Если отношение длин сторон одного треугольника к длинам соответствующих сторон другого треугольника равно k, то периметры этих треугольников тоже удовлетворяют данному соотношению:
| Периметр 1-го треугольника | Периметр 2-го треугольника |
|---|---|
| P1 | P2 |
| a1 + b1 + c1 | a2 + b2 + c2 |
Следовательно, можно сформулировать формулу для нахождения периметра в подобных треугольниках:
P2 = k * P1
Где:
- P1 - периметр первого треугольника
- P2 - периметр второго треугольника
- k - коэффициент, равный отношению длин соответствующих сторон двух подобных треугольников
Используя данную формулу, легко вычислить периметр в подобных треугольниках, если известен периметр одного из них и соотношение длин соответствующих сторон.
Как найти площадь подобных треугольников?
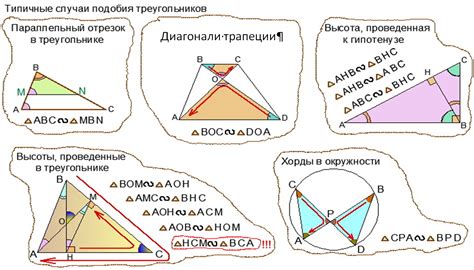
Подобные треугольники имеют одинаковые углы, но могут иметь разные размеры. Чтобы найти площадь подобного треугольника, необходимо знать соотношение сторон между собой.
Для нахождения площади подобных треугольников можно использовать соотношение длин сторон или соотношение площадей.
Соотношение длин сторон: если сторона одного треугольника в k раз меньше стороны другого треугольника, то площадь первого треугольника будет k^2 раз меньше площади второго треугольника.
Соотношение площадей: если площадь одного треугольника равна S1, а площадь другого треугольника равна S2, то площадь первого треугольника будет S1/S2^2 раз меньше площади второго треугольника.
Важно помнить, что для нахождения площади подобных треугольников необходимо знать соотношение между сторонами или площадями треугольников. Это может быть указано в условии задачи или известно из других исходных данных.
Примеры решения задач на нахождение периметра и площади подобных треугольников
1. Задача: Найдите периметр и площадь подобных треугольников, если известно, что их соотношение длин сторон равно 2:3, а сторона меньшего треугольника равна 6 см.
Решение: Пусть x - длина стороны большего треугольника. Так как соотношение длин сторон треугольников равно 2:3, то можно записать пропорцию:
6/x = 2/3
Далее, решая пропорцию, находим x:
x = (6 * 3) / 2 = 9 см
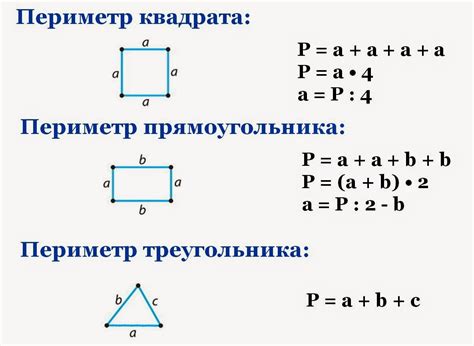
Периметр меньшего треугольника: 6 + 6 + 6 = 18 см
Периметр большего треугольника: 9 + 9 + 9 = 27 см
Площадь меньшего треугольника можно найти по формуле S = (a * h) / 2, где a - основание, а h - высота.
Пусть a = 6 см и h = 4 см (высоту можно найти, используя теорему Пифагора).
S = (6 * 4) / 2 = 12 см²
Так как треугольники подобны, то их площади относятся как квадраты соответствующих сторон:
S1 / S2 = (a1 / a2)²
Подставим известные значения:
S2 / 12 = (9 / 6)²
Находим S2:
S2 = 12 * (9 / 6)² = 27 см²
2. Задача: Два треугольника подобны с коэффициентом подобия 5:7. Найдите периметр и площадь большего треугольника, если сторона меньшего треугольника равна 12 см.
Решение: Пусть x - длина стороны большего треугольника. Так как коэффициент подобия треугольников равен 5:7, можно записать пропорцию:
12/x = 5/7
Далее, решая пропорцию, находим x:
x = (12 * 7) / 5 = 16.8 см
Периметр меньшего треугольника: 12 + 12 + 12 = 36 см
Периметр большего треугольника: 16.8 + 16.8 + 16.8 = 50.4 см
Площадь большего треугольника можно найти по формуле S = (a * h) / 2, где a - основание, а h - высота.
Пусть a = 12 см и h = 8 см (высоту можно найти, используя теорему Пифагора).
S = (12 * 8) / 2 = 48 см²
3. Задача: Известно, что два треугольника подобны с коэффициентом подобия 3:4. Площадь меньшего треугольника равна 36 см². Найдите площадь большего треугольника.
Решение: Пусть S1 - площадь меньшего треугольника, S2 - площадь большего треугольника, a1 - длина стороны меньшего треугольника, a2 - длина стороны большего треугольника.
Так как два треугольника подобны с коэффициентом подобия 3:4, то можно записать пропорцию для площадей:
S1 / S2 = (a1 / a2)²
Подставим известные значения:
36 / S2 = (3 / 4)²
Решая пропорцию, находим S2:
S2 = 36 * (4 / 3)² = 64 см²
4. Задача: Подобные треугольники имеют соотношение длин сторон 2:5. Площадь меньшего треугольника равна 25 см². Найдите площадь большего треугольника.
Решение: Пусть S1 - площадь меньшего треугольника, S2 - площадь большего треугольника, a1 - длина стороны меньшего треугольника, a2 - длина стороны большего треугольника.
Так как треугольники подобны, то их площади относятся как квадраты соответствующих сторон:
S1 / S2 = (a1 / a2)²
Подставим известные значения:
25 / S2 = (2 / 5)²
Решая пропорцию, находим S2:
S2 = 25 * (5 / 2)² = 156.25 см²
Задачи для самостоятельной работы
Решение задач по нахождению периметра и площади в подобных треугольниках требует применения знания об основных свойствах этой геометрической фигуры. Ниже представлены несколько задач, которые помогут закрепить полученные знания и развить навыки самостоятельного решения:
Задача 1. Даны два треугольника ABC и DEF. Известно, что их периметры равны между собой и равны 15 см. Длина стороны AB равна 3 см. Найдите длину стороны DE.
Задача 2. В подобных треугольниках соотношение длин сторон одного треугольника к соответствующим сторонам другого треугольника равно соотношению длин их сторон. Известно, что сторона треугольника ABC равна 5 см, а соответствующая ей сторона треугольника DEF равна 7 см. Найдите длину стороны треугольника DEF.
Задача 3. Даны два подобных треугольника ABC и DEF. Известно, что площадь треугольника ABC равна 36 квадратных см. Найдите площадь треугольника DEF, если отношение площадей подобных треугольников равно квадрату соотношения их сторон.
При решении задач помните о том, что подобные треугольники имеют равные углы и соотношение длин их сторон. Используйте эти свойства, чтобы выразить неизвестные значения и решить задачи. Удачи в самостоятельной работе!
В данной статье мы изучили, как находить периметр и площадь треугольника с помощью подобия.
Периметр подобных треугольников можно найти, умножив длину каждой стороны большего треугольника на коэффициент подобия. Коэффициент подобия можно найти, разделив соответствующие стороны двух треугольников.
Площадь подобных треугольников можно найти, умножив площадь большего треугольника на квадрат коэффициента подобия. Коэффициент подобия можно найти, разделив соответствующие стороны двух треугольников.
Использование подобия треугольников позволяет упростить расчеты периметра и площади, особенно при работе с сложной геометрией. Подобие треугольников позволяет нам применять пропорции и связи между сторонами и углами треугольников для нахождения неизвестных значений.
Таким образом, для нахождения периметра и площади в подобных треугольниках необходимо знать коэффициент подобия и соответствующие стороны треугольников. Это позволяет с легкостью решать задачи с использованием подобия треугольников.
Надеюсь, данная статья помогла вам понять, как находить периметр и площадь в подобных треугольниках и применять это знание в практических задачах.