Периметр круга – это длина окружности, которую можно определить по его радиусу или диаметру. Подсчет периметра круга является важным этапом в геометрии и математике, так как позволяет решать множество задач, связанных с кругами.
Формула для нахождения периметра круга по радиусу представляет собой простое математическое уравнение. Согласно этой формуле, периметр круга равен произведению радиуса на два число пи (π), то есть:
П = 2πR
Где П – периметр, R – радиус круга, π – математическая константа, которая примерно равна 3.14159.
Давайте рассмотрим примеры расчетов периметра круга по его радиусу. Пусть у нас есть круг с радиусом 5 см. Используя формулу, мы можем расчитать его периметр следующим образом:
Периметр круга = 2 * 3.14159 * 5 = 31.4159 см
Таким образом, периметр данного круга составляет 31.4159 см.
Теперь у вас есть понимание о том, как найти периметр круга по его радиусу с помощью простой формулы и вычислить его значение на практике. Помните, что периметр круга можно найти не только по радиусу, но и по диаметру, используя простую формулу и математическую константу π, которая приближенно равна 3.14159.
Радиус круга и его периметр: формула и примеры расчетов
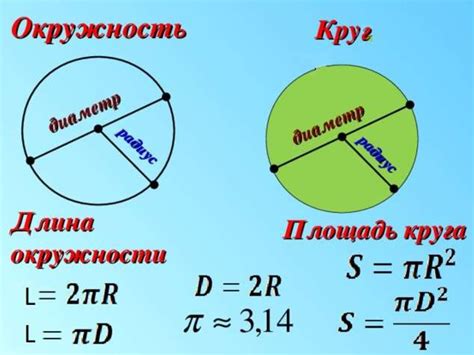
Радиус круга - это линия, соединяющая центр круга с любой точкой на его границе. Радиус обозначается символом "r".
Формула для нахождения периметра круга:
- Посчитайте длину окружности по формуле: P = 2 * π * r.
В данной формуле "π" - это математическая константа, приближенное значение которой равно 3,14. Если вам требуется точное значение "π", используйте большую точность (например, 3,14159).
Пример расчета периметра круга:
- Пусть радиус круга равен 5 см.
- Используя формулу, вычисляем периметр:
P = 2 * 3,14 * 5.
P = 31,4 см.
Таким образом, периметр круга с радиусом 5 см равен 31,4 см.
Зная формулу для нахождения периметра круга, вы можете легко вычислить его для любого заданного радиуса. Эта формула полезна при решении разнообразных задач, связанных с кругами в геометрии или в реальной жизни.
Что такое радиус круга и как его найти?

Для нахождения радиуса круга необходимо знать хотя бы один из следующих параметров:
- Длину окружности;
- Площадь круга;
- Периметр круга.
Формулы для расчета радиуса круга:
- Радиус круга по длине окружности (C):
r = \frac{C}{2\pi}. - Радиус круга по площади (S):
r = \sqrt{\frac{S}{\pi}}. - Радиус круга по периметру (P):
r = \frac{P}{2\pi}.
Примеры расчета радиуса круга:
Дано: длина окружности (C) = 10 см.
Решение: подставляем значение длины окружности (C) в формулу радиуса круга по длине окружности:
r = \frac{10}{2\pi}.Ответ: радиус круга (r) ≈ 1.59 см.
Дано: площадь круга (S) = 20 кв. см.
Решение: подставляем значение площади круга (S) в формулу радиуса круга по площади:
r = \sqrt{\frac{20}{\pi}}.Ответ: радиус круга (r) ≈ 2.83 см.
Дано: периметр круга (P) = 15 см.
Решение: подставляем значение периметра круга (P) в формулу радиуса круга по периметру:
r = \frac{15}{2\pi}.Ответ: радиус круга (r) ≈ 2.39 см.
Формула для расчета периметра круга по радиусу
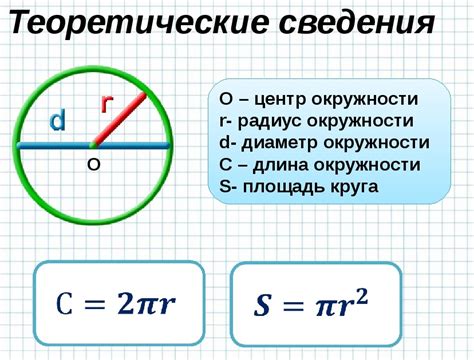
P = 2πr,
где:
- P – периметр круга,
- π (пи) – математическая константа, приближенное значение которой равно 3,14159,
- r – радиус круга.
Для использования формулы необходимо знать радиус круга. Радиус – это расстояние от центра круга до любой его точки. Если вам известен радиус, вы можете легко найти его периметр, применив данную формулу.
Например, пусть радиус круга равен 5 см. Тогда для расчета периметра по формуле:
P = 2πr = 2 * 3,14159 * 5 = 31,4159 см.
Таким образом, периметр круга с радиусом 5 см составляет 31,4159 см.
Зная формулу для расчета периметра круга, вы сможете легко определить длину его границы, имея лишь радиус круга в вашем распоряжении.
Примеры расчета периметра круга по радиусу
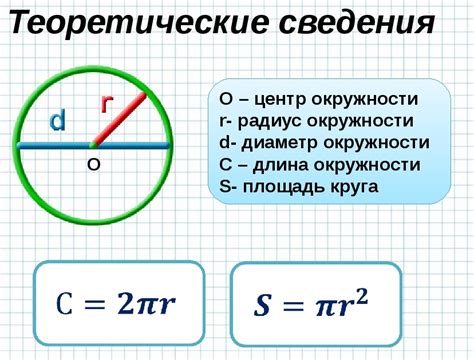
Для расчета периметра круга по радиусу можно использовать следующую формулу:
P = 2πr
Где P - периметр круга, r - радиус круга.
Давайте рассмотрим несколько примеров расчета периметра круга по заданному радиусу:
1. Пусть задан радиус круга r = 5 см. Тогда мы можем использовать формулу для расчета периметра:
P = 2πr = 2π * 5 = 10π ≈ 31.42 см
Таким образом, периметр круга с радиусом 5 см составляет примерно 31.42 см.
2. Рассмотрим случай, когда радиус круга равен 10 см:
P = 2πr = 2π * 10 = 20π ≈ 62.83 см
Таким образом, периметр круга с радиусом 10 см составляет примерно 62.83 см.
3. Для радиуса круга r = 3.5 м:
P = 2πr = 2π * 3.5 = 7π ≈ 21.99 м
Таким образом, периметр круга с радиусом 3.5 м составляет примерно 21.99 м.
Таким образом, зная радиус круга, можно легко рассчитать его периметр, используя соответствующую формулу.
Зачем нужен периметр круга и где применяется этот показатель?

В геометрии периметр круга играет важную роль при решении задач, связанных с определением длины окружности. Например, он помогает определить, сколько проволоки необходимо для изготовления кольца определенного радиуса. Также он применяется при вычислении площади окружности или в других задачах, где необходимо определить длину дуги круга.
Периметр круга имеет важное значение в строительстве и архитектуре. Он помогает определить длину трассы для монорельса, автодороги или железной дороги, проходящей по окружности. Также он используется при проектировании и строительстве круглых зданий, таких как купола, вышки и башни.
Периметр круга также применяется в области географии, при измерении окружности Земли и других небесных объектов. Этот показатель необходим для определения длины экватора и других широтных кругов.
Кроме того, периметр круга имеет практическое применение в повседневной жизни. Например, при покупке ковра или обоев для комнаты нужно знать его длину, чтобы ровно закрепить его по периметру. Также периметр круга может использоваться для определения длины кабеля или шнура, необходимого для обвязки определенного диаметра объекта.
Как видно из примеров, периметр круга является важным показателем, который применяется во многих областях и помогает решать различные практические задачи.
Отличие радиуса и диаметра круга
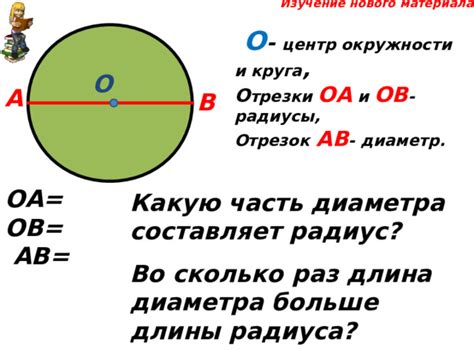
Радиус круга - это расстояние от центра круга до любой его точки на окружности. Он обозначается буквой r или R. Радиус является половиной диаметра и его длина может быть найдена с использованием формулы:
r = D/2
где r - радиус, D - диаметр.
Диаметр круга - это отрезок, соединяющий две точки на окружности, проходящий через центр круга. Он обозначается буквой d или D. Диаметр выражается через радиус следующим образом:
d = 2r
где d - диаметр, r - радиус.
Таким образом, радиус и диаметр круга тесно связаны друг с другом и используются для вычисления различных параметров круга, включая его периметр.