Когда речь заходит о математике, многие из нас ощущают страх и замешательство. Однако, на самом деле, некоторые математические задачи довольно просты в решении, если знать основные формулы и правила. Одним из таких примеров является нахождение периметра квадрата по заданной площади прямоугольника.
Периметр - это сумма всех сторон фигуры, а площадь - это размер поверхности, занимаемой фигурой. Поэтому, чтобы найти периметр квадрата, необходимо знать его площадь. Для начала следует узнать формулу нахождения площади прямоугольника.
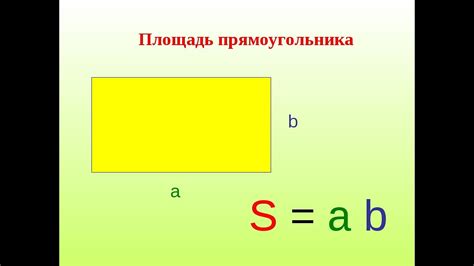
Формула площади прямоугольника: S = a * b
Где S - площадь, a и b - длины сторон прямоугольника. Если известна площадь прямоугольника и одна из его сторон, то можно найти вторую сторону, а затем суммировать все стороны, чтобы получить периметр квадрата.
Давайте рассмотрим пример: пусть площадь прямоугольника равна 36 квадратным единицам, а одна из его сторон равна 6 единицам. Подставим значения в формулу: S = 36, a = 6. Теперь найдем b: 36 = 6 * b. Путем решения этого уравнения получим, что b = 6.
Теперь, чтобы найти периметр квадрата, нужно сложить все стороны прямоугольника. В нашем примере, все стороны равны 6 единицам: 6 + 6 + 6 + 6 = 24. Таким образом, периметр квадрата равен 24 единицам.
Изучение свойств квадрата и прямоугольника
Одно из главных свойств квадрата - равенство его сторон. Таким образом, если известна длина одной стороны квадрата, то можно определить длину остальных сторон. Например, если длина одной стороны квадрата равна 5 см, то все остальные стороны тоже будут равны 5 см.
Для вычисления площади квадрата нужно знать длину его стороны. Площадь квадрата вычисляется путем возведения длины его стороны в квадрат. Например, если длина стороны квадрата равна 5 см, то его площадь будет равна 5 см * 5 см = 25 см2.
Прямоугольник - это фигура с четырьмя сторонами, у которой противоположные стороны равны между собой и все углы прямые, то есть равны 90 градусам.
Прямоугольник также имеет свои уникальные свойства. В отличие от квадрата, у прямоугольника не все стороны равны. Однако, у прямоугольника также можно вычислить площадь и периметр, зная длину его сторон.
Площадь прямоугольника вычисляется путем умножения длины одной из его сторон на длину противоположной стороны. Например, если длина одной стороны прямоугольника равна 5 см, а длина противоположной стороны равна 3 см, то площадь прямоугольника будет равна 5 см * 3 см = 15 см2.
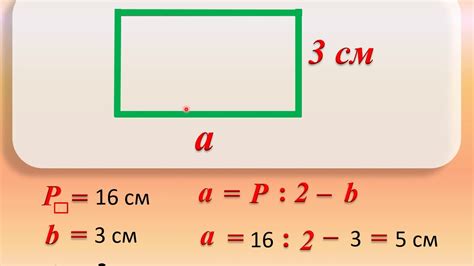
Периметр прямоугольника вычисляется путем сложения длин всех его сторон. Например, если длина одной стороны прямоугольника равна 5 см, а длина противоположной стороны равна 3 см, то периметр прямоугольника будет равен 5 см + 3 см + 5 см + 3 см = 16 см.
Как найти сторону квадрата по площади прямоугольника
Если у вас есть площадь прямоугольника, но вам нужно найти сторону квадрата с такой же площадью, вы можете использовать следующий метод:
1. Вам понадобится значение площади прямоугольника. Предположим, что площадь прямоугольника равна S.
2. Чтобы найти сторону квадрата с такой же площадью, вам нужно найти квадратный корень из площади прямоугольника. Это можно сделать с помощью калькулятора или математической программы.
3. Полученное значение квадратного корня будет равно стороне квадрата, который имеет такую же площадь как и прямоугольник.
Например, если площадь прямоугольника равна 36 квадратным единицам, вы можете найти сторону квадрата следующим образом:
| Площадь прямоугольника (S) | Квадратный корень из площади (сторона квадрата) |
|---|---|
| 36 | 6 |
Таким образом, сторона квадрата с площадью 36 квадратных единиц равна 6 единицам.
Теперь вы знаете, как найти сторону квадрата, если у вас есть площадь прямоугольника. Этот метод может быть полезен, если вам необходимо найти сторону квадрата по известной площади прямоугольника.
Примеры решения задач

Пример 1:
Дано: площадь прямоугольника равна 36 квадратных единиц.
Найдем длину и ширину прямоугольника. Пусть длина равна х, а ширина равна у.
Таким образом, у нас есть два уравнения:
х * у = 36
2 * (х + у) = периметр (квадрата)
Решим первое уравнение относительно у:
у = 36 / х
Подставим это значение во второе уравнение:
2 * (х + (36 / х)) = периметр (квадрата)
Для удобства обозначим периметр квадрата символом п.
Таким образом, у нас есть уравнение:
2 * (х + (36 / х)) = п
Для решения этого уравнения используем метод половинного деления или любой другой подходящий метод. Найденное значение х будет длиной стороны квадрата.
Пример 2:
Дано: площадь прямоугольника равна 64 квадратных единиц.
Найдем длину и ширину прямоугольника. Пусть длина равна х, а ширина равна у.
Таким образом, у нас есть два уравнения:
х * у = 64
2 * (х + у) = периметр (квадрата)
Решим первое уравнение относительно у:
у = 64 / х
Подставим это значение во второе уравнение:
2 * (х + (64 / х)) = периметр (квадрата)
Для удобства обозначим периметр квадрата символом п.
Таким образом, у нас есть уравнение:
2 * (х + (64 / х)) = п
Для решения этого уравнения используем метод половинного деления или любой другой подходящий метод. Найденное значение х будет длиной стороны квадрата.
Практическое применение на практике

Понимание, как найти периметр квадрата по площади прямоугольника, может быть полезно для различных задач в повседневной жизни. Вот несколько примеров, где вы можете применить этот навык:
- Расчет размеров ограждения: Если вы хотите построить ограду вокруг своего участка, то зная площадь прямоугольника, вы сможете вычислить длину каждой стороны квадрата, который будет равен площади прямоугольника. Это поможет вам правильно оценить количество материалов, которые вам понадобятся для постройки ограды.
- Планирование использования пространства: Вы можете использовать знание о периметре квадрата, чтобы оптимизировать использование пространства в комнате или на участке. Например, если вы хотите разместить мебель в комнате, зная площадь прямоугольника, вы сможете определить оптимальные размеры квадратного ковра или других предметов, чтобы они идеально вписывались в пространство.
- Расчет объема материала: Если у вас есть прямоугольный объект, и вы хотите знать, сколько материала вам понадобится для его покрытия или наполнения, вы можете использовать знание о площади прямоугольника, чтобы вычислить необходимый объем материала.
- Определение стоимости: Если вам нужно покрасить стены комнаты или покрыть пол ламинатом, зная площадь прямоугольника, вы сможете оценить стоимость материалов, которые вам понадобятся. Это поможет вам планировать бюджет и сделать правильные финансовые решения.
Все эти примеры демонстрируют практическое применение знания о периметре квадрата по площади прямоугольника. Понимая этот метод, вы сможете эффективно использовать свои знания во многих ситуациях в повседневной жизни.