Периметр квадрата – одна из важнейших характеристик этой геометрической фигуры. Но как быть, если квадрат имеет неровные стороны? Не стоит отчаиваться – мы расскажем, как найти периметр неровного квадрата и предоставим примеры решений.
Перед тем как разобрать способы расчета периметра, важно помнить определение квадрата. Это геометрическая фигура, у которой все стороны равны между собой. Однако в некоторых случаях стороны могут иметь разную длину, создавая неровную форму.
Для расчета периметра неровного квадрата можно воспользоваться простым способом. Суммируйте длины всех четырех сторон, чтобы получить значение периметра. Допустим, у вас есть квадрат, у которого длины сторон равны 5 см, 7 см, 5 см и 7 см. Чтобы найти периметр, сложите все значения: 5 + 7 + 5 + 7 = 24 см. Полученное число и будет периметром неровного квадрата.
Неровные квадраты: определение и примеры
Примеры неровных квадратов можно найти в повседневной жизни. Например, прямоугольный школьный стол может быть считаться неровным квадратом, если его стороны не являются точно равными. Еще одним примером может служить несимметричный клетчатый коврик, где стороны квадрата имеют разные длины.
Чтобы найти периметр неровного квадрата, необходимо сложить длины всех его сторон. Например, если сторона квадрата А равна 5 метров, а сторона квадрата Б равна 7 метров, то периметр неровного квадрата будет равен 5 + 7 + 5 + 7 = 24 метра.
Таким образом, неровные квадраты представляют собой особую разновидность четырехугольников, где стороны могут быть неравными. Их периметр можно вычислить, сложив длины всех сторон. Примеры неровных квадратов можно встретить в различных сферах нашей жизни.
Что такое неровный квадрат?

Неровные квадраты могут иметь различные пропорции сторон и углы. Это выглядит нестандартно и привлекает внимание. Эти фигуры могут представлять собой интересные геометрические задачи и вызывать сложности при вычислении их характеристик, таких как площадь и периметр.
Решение задачи нахождения периметра неровного квадрата требует вычисления суммы всех его сторон. Это может быть выполнено с использованием формулы или путем измерения каждой стороны и последующего сложения результатов.
Примеры неровных квадратов

- Квадратное озеро. Некоторые озера имеют форму квадрата, но их береговая линия не является ровной, а образует некоторую волнистую или заостренную форму.
- Городская площадь. Некоторые площади, такие как Площадь Республики в Минске, имеют форму неровного квадрата из-за наличия фонтанов, скульптур, архитектурных элементов и других объектов.
- Мозаика на полу. В некоторых зданиях и даже на улицах можно увидеть мозаичные плитки, которые образуют форму неровного квадрата.
- Архитектурные элементы. Некоторые здания могут иметь фасады или окна, которые образуют форму неровного квадрата.
Это лишь некоторые примеры, и на самом деле, неровные квадраты могут быть найдены во многих других местах. Считается, что неровные квадраты добавляют особый характер и интригу к искусству и архитектуре.
Как найти периметр неровного квадрата: простые формулы
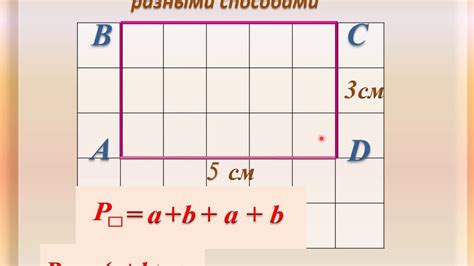
Периметр квадрата - это сумма всех его сторон. В случае неровного квадрата, нам нужно найти сумму всех четырех сторон. Для этого можно использовать простую формулу:
| Формула | Пример |
|---|---|
| Периметр = Сторона1 + Сторона2 + Сторона3 + Сторона4 | Периметр = 4 см + 5 см + 4 см + 5 см = 18 см |
Пример выше показывает, как найти периметр неровного квадрата, используя значения сторон в сантиметрах. Для решения подобных задач необходимо знать длины всех четырех сторон квадрата.
В случае, если известны только некоторые стороны квадрата, можно использовать другую простую формулу, основанную на свойстве квадрата:
| Формула | Пример |
|---|---|
| Периметр = 2 * (Сторона1 + Сторона2) | Известно: Сторона1 = 3 м, Сторона2 = 4 м |
| Периметр = 2 * (3 м + 4 м) = 14 м |
Эту формулу можно использовать, если известны значения только двух сторон. При этом сумма этих двух сторон умножается на 2, так как все стороны неровного квадрата имеют одинаковую длину.
Итак, нахождение периметра неровного квадрата требует знания длин всех его сторон. Если известны все стороны, можно использовать первую простую формулу. В случае, если известны только две стороны, можно применить вторую формулу.
Формула для вычисления периметра неровного квадрата
Периметр неровного квадрата можно вычислить с помощью формулы, основанной на длине его сторон. Чтобы найти периметр, нужно сложить длины всех четырех сторон квадрата.
| Сторона | Длина |
|---|---|
| Сторона 1 | а |
| Сторона 2 | b |
| Сторона 3 | c |
| Сторона 4 | d |
Таким образом, формула для вычисления периметра неровного квадрата имеет вид:
Периметр = a + b + c + d
Где а, b, c и d - длины сторон квадрата.
Эта формула позволяет легко найти периметр неровного квадрата, используя известные значения длин его сторон. Важно, чтобы все измерения были выражены в одной и той же единице измерения, например, в сантиметрах или метрах.
Пример вычисления периметра неровного квадрата
Для вычисления периметра неровного квадрата необходимо знать длины всех его сторон. Допустим, у нас есть неровный квадрат со сторонами a, b, c и d. Чтобы найти периметр, нужно сложить длины всех сторон:
| Сторона | Длина |
|---|---|
| a | 5 см |
| b | 7 см |
| c | 5 см |
| d | 7 см |
Таким образом, периметр неровного квадрата можно найти по формуле:
Периметр = a + b + c + d
Подставляя значения сторон, получим:
Периметр = 5 см + 7 см + 5 см + 7 см = 24 см
Таким образом, периметр данного неровного квадрата равен 24 см.