Описанная окружность четырехугольника - это окружность, которая проходит через все вершины этого четырехугольника. Нахождение периметра описанной окружности четырехугольника является важной задачей в геометрии и может использоваться в различных областях, включая архитектуру, строительство и механику. В этой статье мы рассмотрим простые и понятные шаги для нахождения периметра описанной окружности четырехугольника.
Периметр описанной окружности четырехугольника можно найти, используя формулу, которая связывает радиус описанной окружности и длины сторон четырехугольника. Для начала, нам понадобятся измерения сторон и углов четырехугольника, чтобы вычислить длины сторон и определить радиус описанной окружности.
Далее, мы можем использовать теорему тангенсов для нахождения радиуса описанной окружности четырехугольника. Теорема тангенсов утверждает, что квадраты тангенсов половины углов, составляющих четырехугольник, равны отношению произведения длин противоположных сторон к произведению длин смежных сторон.
Наконец, после нахождения радиуса описанной окружности четырехугольника, мы можем найти периметр путем умножения радиуса на 2π. Таким образом, мы получим искомый ответ и сможем легко вычислить периметр описанной окружности четырехугольника.
Определение описанной окружности
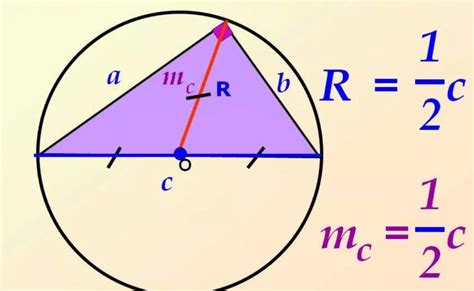
Для начала, нужно найти середину сторон четырехугольника путем нахождения среднего арифметического координат противоположных вершин. Затем, используя эти середины сторон, можно найти середину диагоналей четырехугольника.
Далее, необходимо найти расстояние от середины диагоналей до каждой вершины четырехугольника. Это расстояние является радиусом описанной окружности.
Знание формулы для расчета периметра

Формула для расчета периметра описанного окружности четырехугольника выглядит следующим образом:
Периметр = a + b + c + d
где a, b, c и d - длины сторон четырехугольника.
Чтобы найти периметр описанной окружности, нужно знать длины всех сторон четырехугольника. Если стороны заданы, то достаточно просто сложить их значения по формуле.
Знание формулы для расчета периметра поможет вам правильно провести вычисления и получить точный результат.
Построение четырехугольника
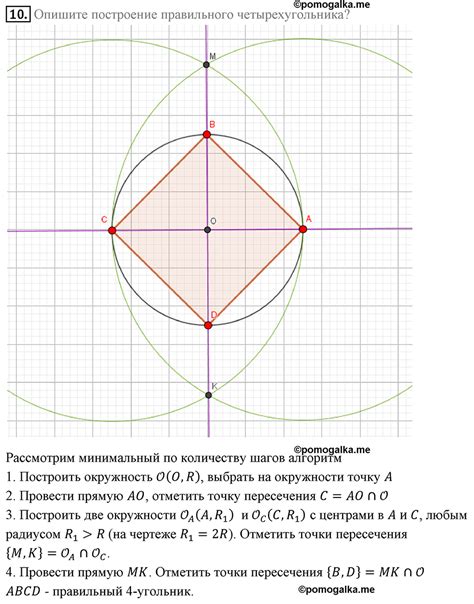
Чтобы построить четырехугольник, требуется выполнить следующие шаги:
- Начните с определения типа четырехугольника. Он может быть выпуклым, невыпуклым или пересекающимся.
- Проведите линии, соединяющие вершины четырехугольника. Убедитесь, что линии не пересекаются, иначе это будет означать, что вы ошиблись при построении четырехугольника.
- Измерьте длины сторон и углы четырехугольника. Для этого можно использовать линейку и угломер.
- Проверьте, соответствует ли измеренная информация требованиям периметра четырехугольника. Периметр равен сумме длин всех четырех сторон.
Важно помнить, что для получения корректных результатов необходимо строго соблюдать все указанные шаги при построении четырехугольника.
Пример построения и измерения сторон и углов четырехугольника показан в таблице ниже:
| Сторона | Длина | Угол |
|---|---|---|
| AB | 5 см | 90° |
| BC | 4 см | 110° |
| CD | 6 см | 70° |
| DA | 7 см | 90° |
После выполнения всех указанных шагов можно приступить к нахождению периметра четырехугольника.
Нахождение длин сторон четырехугольника

Для нахождения периметра описанного окружности четырехугольника нам необходимо знать длины всех его сторон. Давайте рассмотрим, как можно найти эти длины.
Существует несколько способов нахождения длин сторон четырехугольника, в зависимости от доступных исходных данных. Рассмотрим два наиболее распространенных случая:
- Когда известны координаты вершин четырехугольника
- Когда известны длины диагоналей и углы четырехугольника
1. Когда известны координаты вершин четырехугольника
В этом случае мы можем использовать формулу расстояния между двумя точками, чтобы найти длины всех сторон четырехугольника. Для этого нужно вычислить расстояние между каждой парой вершин.
Предположим, что наши вершины имеют координаты (x1, y1), (x2, y2), (x3, y3) и (x4, y4). Тогда длина стороны AB будет равна:
{вставка формулы}
Аналогичным образом можно найти длины сторон BC, CD и DA. После нахождения всех сторон, их нужно просуммировать, чтобы получить периметр.
2. Когда известны длины диагоналей и углы четырехугольника
Если у нас известны длины диагоналей (AC и BD) и углы (A, B, C и D), то мы можем использовать закон косинусов для нахождения длин сторон четырехугольника.
Для примера, рассмотрим сторону AB. Мы можем использовать закон косинусов следующим образом:
{вставка формулы}
Аналогичным образом можно найти длины сторон BC, CD и DA. После нахождения всех сторон, их нужно просуммировать, чтобы получить периметр.
Итак, в зависимости от доступных данных мы можем использовать различные методы для нахождения длин сторон четырехугольника. Важно помнить, что точность и правильность результатов зависит от точности исходных данных и выбранного метода вычислений.
Нахождение радиуса описанной окружности

Чтобы найти радиус описанной окружности четырехугольника, нужно знать длины его сторон и/или диагоналей. Существует несколько способов расчета радиуса:
- Если известны длины сторон четырехугольника (a, b, c, d), можно использовать формулу радиуса описанной окружности:
- Если известны диагонали четырехугольника (p, q), можно использовать следующую формулу:
- Если известны углы четырехугольника и одна из его диагоналей (p), можно использовать формулу:
R = (a * b * c * d) / (4 * S), где S - площадь четырехугольника, которую можно найти по формуле Герона или другому способу, зависящему от известных данных.
R = (p * q) / (4 * S), где S - площадь четырехугольника, которую можно найти с помощью формулы Герона или другого способа.
R = (p / 2) * tg(A) * tg(B) * tg(C) * tg(D), где A, B, C, D - углы четырехугольника, их можно выразить через угловые суммы или известные углы.
После нахождения радиуса описанной окружности четырехугольника, можно использовать его значение для нахождения периметра описанной окружности, с помощью формулы:
П = 2 * π * R, где π (пи) - математическая константа, приближенное значение которой равно 3.14 или 22/7.
Теперь, зная радиус описанной окружности, можно легко находить периметр четырехугольника и использовать эту информацию для решения задач по геометрии.
Нахождение длины окружности
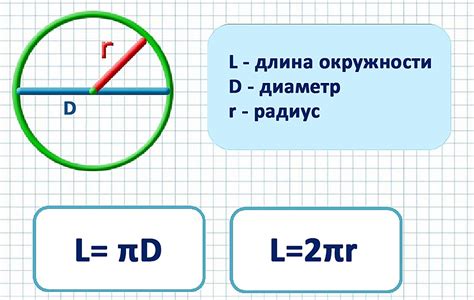
Для нахождения длины окружности, описанной вокруг четырехугольника, необходимо знать радиус этой окружности. Радиус окружности можно вычислить, зная длины ее сторон и углы между ними. После нахождения радиуса окружности, можно легко вычислить ее длину по формуле.
Формула для нахождения длины окружности: Длина окружности = 2πr, где π (пи) – это математическая константа, примерное значение которой равно 3,14159.
Для вычисления значения длины окружности, необходимо умножить радиус окружности на 2π. Это даст нам значение в определенных единицах длины (например, сантиметрах или дюймах).
Пример: Пусть у нас есть четырехугольник со сторонами длиной 5, 6, 7 и 8 единиц, и он описан около окружности. Чтобы найти радиус окружности, сначала найдем полупериметр четырехугольника (сумму всех его сторон, разделенную на 2):
Полупериметр = (5 + 6 + 7 + 8) / 2 = 13 единиц
Затем используем следующую формулу для нахождения радиуса окружности:
Радиус = Полупериметр / 2π = 13 / (2 * 3.14159) ≈ 2.07080 единиц
Теперь, чтобы найти длину окружности, умножим радиус на 2π:
Длина окружности ≈ 2 * 3.14159 * 2.07080 ≈ 13.050 единиц
Таким образом, длина описанной окружности четырехугольника составляет около 13.050 единиц.
Суммирование всех сторон для получения итогового значения периметра

Чтобы найти периметр описанной окружности четырехугольника, нужно сложить длины всех его сторон.
Для этого:
- Определите длины всех сторон четырехугольника.
- Сложите длины всех сторон.
- Полученная сумма будет итоговым значением периметра.
Например, если четырехугольник имеет стороны длиной 5, 7, 9 и 6 единиц, то периметр будет равен 5 + 7 + 9 + 6 = 27 единиц.
Таким образом, суммирование всех сторон поможет нам найти периметр описанной окружности четырехугольника.