Периметр геометрической фигуры является одной из основных характеристик, определяющих ее размеры и форму. Он позволяет рассчитать длину внешней границы фигуры и выразить ее в единицах измерения.
Если геометрическая фигура представлена в виде клеточек, то поиск ее периметра может показаться сложной задачей. Однако существуют несколько методов, которые помогут справиться с этим дилеммой с минимальными усилиями.
Первый метод основан на подсчете длины каждой стороны фигуры в клетках и их последующем сложении. Для этого необходимо просто пройти вокруг фигуры, посчитав при этом длину каждой стороны.
Пример: Рассмотрим прямоугольник, состоящий из 4 клеток по ширине и 3 клеток по высоте. Для подсчета периметра необходимо сложить длины всех сторон: (4+4) + (3+3) + (4+4) + (3+3) = 28.
Методы для нахождения периметра по клеточкам геометрической фигуры
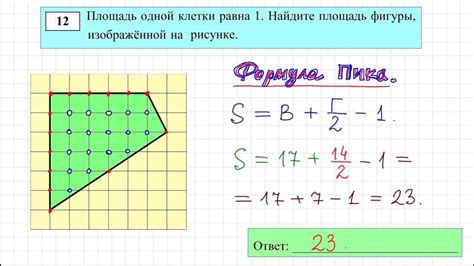
Периметр геометрической фигуры определяется суммой длин всех ее сторон. При работе с клеточными геометрическими фигурами, периметр можно определить с использованием различных методов.
Один из методов для нахождения периметра по клеточкам геометрической фигуры - это подсчет длин границ клеток. Для этого необходимо обойти все границы фигуры и сложить длины границ, помечая уже посещенные клетки, чтобы избежать двойного учета. Этот метод особенно полезен при работе с фигурами, состоящими из прямоугольников или квадратов.
Еще один метод основывается на подсчете числа клеток на каждой стороне фигуры и их сложении. Для этого можно использовать формулу P = a + b + c + d, где a, b, c, d - количество клеток на каждой стороне фигуры. Этот метод подходит для разнообразных геометрических фигур, таких как треугольники, многоугольники и другие. Важно правильно определить границы фигуры для точного подсчета.
Также можно использовать метод, основанный на подсчете смежных клеток для каждой клетки фигуры. Начиная с выбранной клетки, необходимо проверить ее соседей и добавить к периметру клеток те, которые являются границей фигуры. При этом также следует помечать уже посещенные клетки, чтобы избежать повторного подсчета. Данный метод позволяет точно определить периметр сложных фигур с различными контурами.
Использование формулы для прямоугольника
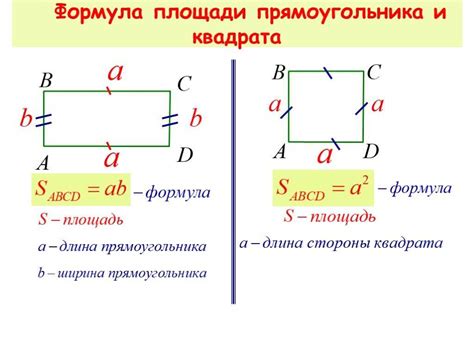
Периметр прямоугольника равен удвоенной сумме длины его сторон:
| Формула |
|---|
| Периметр = 2 * (длина + ширина) |
Допустим, у нас есть прямоугольник со сторонами длиной 4 клетки и шириной 6 клеток. Чтобы найти его периметр, мы просто применяем формулу, подставляя значения:
| Формула |
|---|
| Периметр = 2 * (4 + 6) = 2 * 10 = 20 клеток |
Таким образом, периметр нашего прямоугольника составляет 20 клеток.
Использование этой формулы позволяет легко находить периметр прямоугольников разных размеров, что делает ее очень полезной при работе с клеточными геометрическими фигурами.
Расчет периметра треугольника по его сторонам
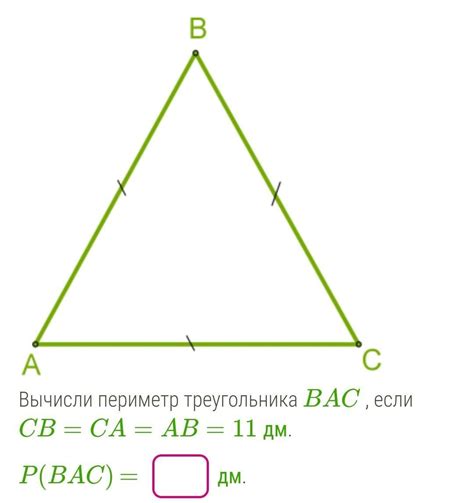
Пусть треугольник имеет стороны a, b и c. Для расчета его периметра используем формулу:
Периметр (P) = a + b + c
Для примера, рассмотрим треугольник со сторонами a = 5, b = 4 и c = 3. Чтобы найти его периметр:
Периметр (P) = 5 + 4 + 3 = 12
Таким образом, периметр треугольника со сторонами 5, 4 и 3 равен 12.
Зная длины всех сторон, можно легко расчитать периметр треугольника по данной формуле.
Алгоритм нахождения периметра многоугольника

Для начала, необходимо перечислить координаты всех вершин многоугольника. Это можно сделать в виде таблицы, где каждая строка будет содержать пару значений - координаты точки по оси X и Y. Например:
- (x₁, y₁)
- (x₂, y₂)
- (x₃, y₃)
- ...
Далее, следует использовать формулу для нахождения расстояния между двумя точками в декартовой системе координат:
расстояние = √((x₂ - x₁)² + (y₂ - y₁)²)
Где (x₁, y₁) и (x₂, y₂) - координаты двух соседних вершин.
Используя эту формулу, нужно вычислить расстояние для каждой пары соседних вершин и затем сложить все полученные значения. В итоге получится сумма длин сторон многоугольника - его периметр.
Применение данного алгоритма требует знания координат всех вершин многоугольника и их порядка обхода. Однако, в некоторых случаях, можно использовать специальное программное обеспечение или библиотеки, которые позволяют автоматически вычислить периметр многоугольника по его геометрическому описанию или графическому представлению.