Периметр прямоугольника является важной характеристикой этой геометрической фигуры. Он позволяет измерить длину окружности, образуемой вокруг прямоугольника, и является суммой всех его сторон. Найти периметр прямоугольника можно по простой формуле, которую запомнить очень просто.
Формула для нахождения периметра прямоугольника:
P = 2a + 2b
Где P - периметр прямоугольника, а a и b - длины его сторон.
Рассмотрим пример. Допустим, у нас есть прямоугольник с длиной одной стороны a = 5 см и длиной другой стороны b = 8 см. Чтобы найти периметр, мы подставляем значения a = 5 и b = 8 в формулу:
P = 2 * 5 + 2 * 8 = 10 + 16 = 26
Таким образом, периметр прямоугольника равен 26 см.
Теперь, когда вы знаете формулу и принцип нахождения периметра прямоугольника, вы сможете расчитывать его значение без труда. Эта информация пригодится вам во многих сферах жизни, начиная от строительства и дизайна до математики и ежедневных расчетов.
Что такое периметр прямоугольника?
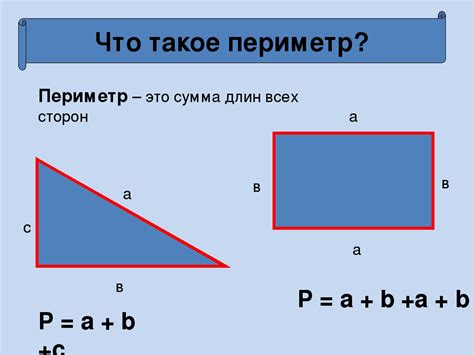
Формула для нахождения периметра прямоугольника имеет вид: P = 2a + 2b, где a и b - длины двух сторон прямоугольника.
Например, если стороны прямоугольника равны 5 и 10, то периметр можно вычислить следующим образом: P = 2 * 5 + 2 * 10 = 10 + 20 = 30.
Зная периметр прямоугольника, можно определить, насколько длинным должен быть периметр, чтобы он соответствовал заданным условиям или требованиям. Например, периметр может не превышать определенное значение или быть равным заданной величине.
Знание формулы для нахождения периметра прямоугольника позволяет решать различные задачи, связанные с геометрией и измерением длин. Эта информация может быть полезна в повседневной жизни, в строительстве, а также при решении различных математических задач и задач на программирование.
Определение и общие сведения

Формула для расчета периметра прямоугольника равна:
Периметр = 2 * (Длина + Ширина)
Где Длина - длина прямоугольника, а Ширина - ширина прямоугольника.
Например, если длина прямоугольника равна 5 см, а ширина равна 3 см, то периметр прямоугольника будет:
Периметр = 2 * (5 + 3) = 16 см.
Формула для расчета периметра прямоугольника
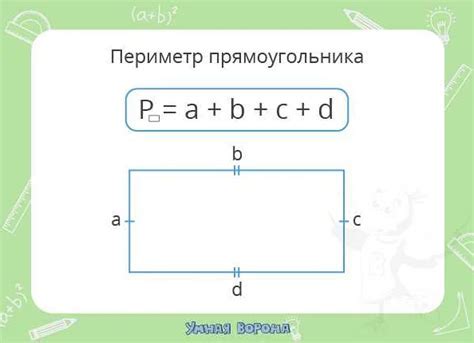
П = 2 * (a + b)
Например, если длина стороны прямоугольника равна 5 см, а ширина - 3 см:
| Длина стороны (см) | Ширина стороны (см) | Периметр (см) |
|---|---|---|
| 5 | 3 | 16 |
Таким образом, для прямоугольника со сторонами 5 см и 3 см, периметр будет равен 16 см.
Пример 1: Нахождение периметра прямоугольника с известными сторонами

Рассмотрим пример нахождения периметра прямоугольника, если известны его стороны.
Пусть дан прямоугольник со сторонами a = 6 см и b = 8 см. Чтобы найти его периметр, нужно сложить все его стороны.
Используем формулу для нахождения периметра прямоугольника: P = 2a + 2b.
| Стороны прямоугольника | Периметр |
|---|---|
| a = 6 см, b = 8 см | P = 2 * 6 см + 2 * 8 см |
| a = 6 см, b = 8 см | P = 12 см + 16 см |
| a = 6 см, b = 8 см | P = 28 см |
Таким образом, периметр прямоугольника со сторонами a = 6 см и b = 8 см равен 28 см.
Пример 2: Нахождение периметра прямоугольника по координатам вершин

В данном примере рассмотрим, как найти периметр прямоугольника, зная координаты его вершин. Для этого нам потребуется знание основ геометрии и формулы для вычисления длин сторон прямоугольника.
Допустим, у нас имеются координаты вершин прямоугольника, заданные как (x1, y1), (x2, y2), (x3, y3) и (x4, y4), где каждая вершина имеет свои координаты на плоскости.
Чтобы найти периметр прямоугольника, необходимо вычислить сумму длин его сторон. Длина стороны прямоугольника может быть найдена с помощью теоремы Пифагора.
Следуя алгоритму, можно вычислить длины всех четырех сторон прямоугольника, а затем просуммировать их для получения периметра.
Алгоритм:
- Вычисляем длины всех четырех сторон прямоугольника:
- Длина первой стороны: √((x2 - x1)² + (y2 - y1)²)
- Длина второй стороны: √((x3 - x2)² + (y3 - y2)²)
- Длина третьей стороны: √((x4 - x3)² + (y4 - y3)²)
- Длина четвертой стороны: √((x1 - x4)² + (y1 - y4)²)
Например, пусть у нас есть прямоугольник с координатами вершин (0, 0), (0, 4), (5, 4) и (5, 0). Мы можем применить формулу для каждой стороны прямоугольника и получить следующие длины:
- Длина первой стороны: √((0 - 0)² + (4 - 0)²) = √(0 + 16) = √16 = 4
- Длина второй стороны: √((5 - 0)² + (4 - 4)²) = √(25 + 0) = √25 = 5
- Длина третьей стороны: √((5 - 5)² + (0 - 4)²) = √(0 + 16) = √16 = 4
- Длина четвертой стороны: √((0 - 5)² + (0 - 0)²) = √(25 + 0) = √25 = 5
Затем, суммируя все длины сторон, мы получим периметр прямоугольника:
Периметр = 4 + 5 + 4 + 5 = 18
Таким образом, периметр данного прямоугольника составляет 18 единиц длины.
Свойства периметра прямоугольника

Свойства периметра прямоугольника:
1. Симметрия: Периметр прямоугольника имеет симметрию относительно всех своих сторон. Это означает, что если прямоугольник перевернуть на 180 градусов вокруг любой своей стороны, его периметр останется неизменным.
2. Зависимость от сторон: Периметр прямоугольника зависит от длин его сторон. Чем больше длина сторон, тем большим будет периметр. Если сторона удлиняется или укорачивается, периметр также изменяется.
3. Измерение длины: Периметр прямоугольника измеряется в единицах длины, таких как сантиметры, метры или футы.
4. Измерение площади: Периметр прямоугольника не является мерой его площади. Периметр отражает только длину границы прямоугольника, а площадь показывает его покрытие, то есть количество площади внутри фигуры.
5. Равенство диагоналей: Для прямоугольника со сторонами a и b диагонали равны и определяются по формуле d = √(a² + b²). Периметр равен d·2.
Изучение свойств периметра прямоугольника помогает понять его характеристики и использовать его в различных математических и практических задачах.
Как использовать периметр прямоугольника в повседневной жизни

Знание понятия периметра прямоугольника может быть полезным в различных аспектах повседневной жизни. Рассмотрим несколько примеров:
1. Строительство и ремонт
При планировании строительства или ремонта часто требуется расчет и закупка материалов, например, покупка обоев, плитки или ламината для отделки пола. Зная периметр прямоугольного помещения, можно точно рассчитать количество необходимых материалов и избежать недостатка или перерасхода.
2. Садоводство и огородничество
Ведение сада или огорода тоже требует расчетов: купить достаточное количество ограждения для забора, высчитать площадь грядок для посева или посадки растений. Зная периметр прямоугольного участка земли или грядки, можно определить необходимые затраты и приступить к планированию.
3. Дизайн интерьера
При планировании интерьера комнаты, например, при выборе мебели, ковра или занавесок, важно учесть размеры и форму помещения. Зная периметр прямоугольника стены или комнаты, можно подобрать мебель и аксессуары, которые гармонично впишутся в пространство и не будут перегружать его.
Периметр прямоугольника - это не просто абстрактная математическая формула, а удобный инструмент, который может пригодиться в быту, работе или хобби. Рассмотренные примеры демонстрируют, что знание периметра позволяет производить точные расчеты, экономить ресурсы и создавать гармоничные решения в различных сферах жизни.
Прямоугольник и его периметр в геометрических задачах
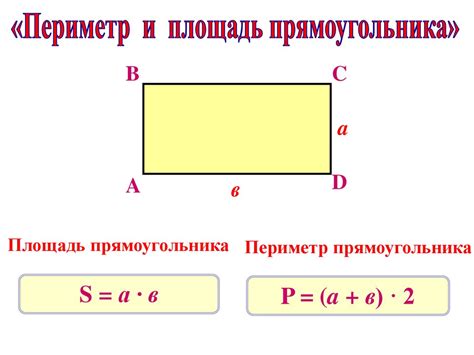
Периметр прямоугольника - это сумма длин всех его сторон. Для нахождения периметра прямоугольника используется следующая формула:
Периметр = 2a + 2b
где a и b - длины сторон прямоугольника.
Например, если длина одной стороны прямоугольника равна 5, а длина другой стороны равна 8, то периметр прямоугольника можно найти следующим образом:
Периметр = 2 * 5 + 2 * 8 = 10 + 16 = 26
Таким образом, периметр прямоугольника со сторонами длиной 5 и 8 будет равен 26.
Периметр прямоугольника является важной характеристикой фигуры, так как он позволяет определить, сколько материала будет необходимо для ограждения прямоугольного участка или постройки.