Периметр – одно из основных понятий геометрии. Он представляет собой сумму длин всех сторон фигуры. В математике есть различные формулы для вычисления периметра различных фигур, и в этой статье мы рассмотрим, как найти периметр прямоугольного треугольника.
Прямоугольный треугольник – это треугольник, у которого один из углов равен 90 градусам. Такой треугольник имеет два катета и гипотенузу, которая является его самой длинной стороной. Катеты – это стороны треугольника, которые образуют прямой угол.
Для вычисления периметра прямоугольного треугольника по двум катетам (a и b), необходимо сложить длины всех его сторон, то есть длину каждого катета и гипотенузу:
P = a + b + c,
где P – периметр треугольника, a и b – длины катетов, а c – длина гипотенузы.
После того, как вы найдете длины катетов и гипотенузы, просто сложите их и получите ответ – периметр прямоугольного треугольника по двум катетам. Не забывайте следить за правильностью вычислений и единицами измерения.
Как найти периметр прямоугольного треугольника
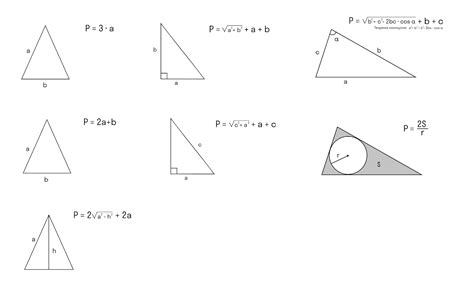
Формула для вычисления периметра прямоугольного треугольника:
P = a + b + c
Где:
- P - периметр треугольника;
- a и b - длины катетов треугольника;
- c - длина гипотенузы треугольника.
Для нахождения периметра прямоугольного треугольника нужно сложить длины всех его сторон. Катеты задаются в условии задачи, а гипотенузу можно найти с помощью теоремы Пифагора.
Теорема Пифагора гласит:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, c^2 = a^2 + b^2.
Зная длины катетов a и b, можно найти длину гипотенузы c и, следовательно, вычислить периметр треугольника по формуле P = a + b + c.
Не забывайте, что периметр выражается в единицах длины, указанных в условии задачи (например, сантиметрах или метрах).
Периметр прямоугольного треугольника - базовые сведения
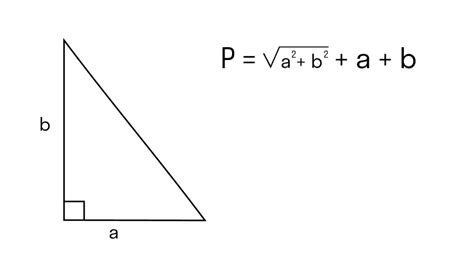
Катеты прямоугольного треугольника - это два из его трех сторон, образующих прямой угол. Обозначаются они буквами a и b. Третьей стороной является гипотенуза, обозначаемая буквой c.
Для нахождения периметра прямоугольного треугольника можно воспользоваться формулой:
P = a + b + c
где P - периметр, a и b - длины катетов, c - длина гипотенузы.
Важно помнить, что катеты и гипотенуза прямоугольного треугольника связаны между собой формулой Пифагора:
c^2 = a^2 + b^2
С помощью этой формулы можно выразить гипотенузу c через катеты a и b, и затем использовать полученное значение для расчета периметра.
Пример:
- Даны катеты a = 3 и b = 4, по формуле Пифагора найдем гипотенузу:
- c^2 = 3^2 + 4^2 = 9 + 16 = 25
- c = √25 = 5
- Теперь можем найти периметр:
- P = 3 + 4 + 5 = 12
Таким образом, периметр прямоугольного треугольника с катетами 3 и 4 равен 12.
Формула для вычисления периметра прямоугольного треугольника
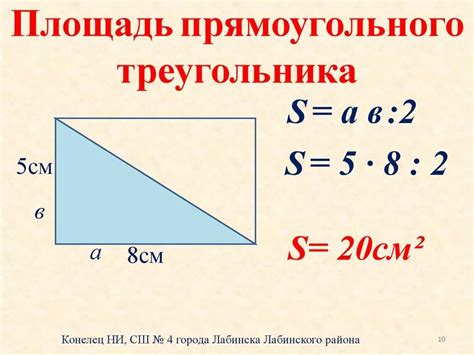
Периметр = а + b + c,
где а и b - длины катетов треугольника, а с - длина гипотенузы.
Для расчета периметра прямоугольного треугольника необходимо знать значения длин обоих катетов. Длину катетов можно найти по теореме Пифагора, зная длину гипотенузы и один из катетов:
Если известна длина гипотенузы c и одного из катетов а, то длину второго катета b можно найти по формуле:
b = √(c^2 - a^2).
Таким образом, имея значения длин обоих катетов, можно подставить их в формулу для периметра, чтобы найти значение периметра прямоугольного треугольника.
Например, если длина первого катета а равна 3, а длина второго катета b равна 4, то длину гипотенузы c можно найти по формуле Пифагора: c = √(3^2 + 4^2) = 5. Затем, подставляя значения длин катетов и гипотенузы в формулу для периметра, получим: Периметр = 3 + 4 + 5 = 12.
Таким образом, формула для вычисления периметра прямоугольного треугольника позволяет быстро и легко найти значение периметра по известным длинам катетов.
Пример вычисления периметра прямоугольного треугольника
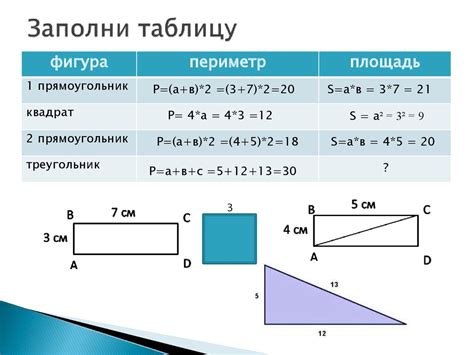
Чтобы найти периметр прямоугольного треугольника, нужно знать длину его двух катетов. Давайте рассмотрим пример:
- Пусть у нас есть прямоугольный треугольник ABC, где AB и BC - катеты, AC - гипотенуза.
- Предположим, что длина катета AB равна 4, а длина катета BC равна 3.
- Чтобы найти периметр, нужно сложить длины всех трех сторон треугольника.
- Периметр P равен сумме длин катетов и гипотенузы: P = AB + BC + AC.
- Зная, что катеты AB и BC равны 4 и 3 соответственно, можем подставить значения в формулу:
P = 4 + 3 + AC
Так как треугольник прямоугольный, то по теореме Пифагора длина гипотенузы AC равна:
AC = √(AB² + BC²)
Подставляем известные значения:
AC = √(4² + 3²)
AC = √(16 + 9)
AC = √25
AC = 5
Теперь, зная длину всех сторон треугольника, можем вычислить его периметр:
P = 4 + 3 + 5 = 12
Таким образом, периметр прямоугольного треугольника с катетами длиной 4 и 3 равен 12.
Важные советы при вычислении периметра прямоугольного треугольника

- Перед началом вычислений убедитесь, что треугольник действительно прямоугольный. Это можно проверить с помощью теоремы Пифагора, где сумма квадратов катетов должна быть равна квадрату гипотенузы.
- Измерьте длины обоих катетов треугольника с помощью линейки или другого инструмента, гарантирующего точность измерения. Обычно катеты обозначаются буквами a и b.
- Используйте формулу для нахождения периметра прямоугольного треугольника: периметр = a + b + гипотенуза.
- Для вычисления гипотенузы треугольника можно воспользоваться теоремой Пифагора: гипотенуза = √(a^2 + b^2), где a и b - длины катетов.
- Проверьте свои вычисления, чтобы избежать ошибок. Для этого можно использовать калькулятор или проверить свои результаты с помощью проверенного решения.
- Не забывайте указывать единицы измерения при указании ответа. Например: "Периметр треугольника равен 24 см."
Следуя этим важным советам, вы сможете правильно вычислить периметр прямоугольного треугольника и получить точный результат.
Как использовать периметр прямоугольного треугольника в практических задачах
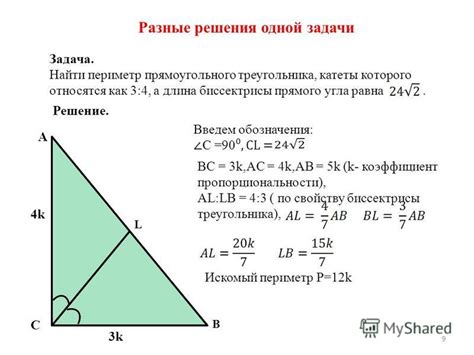
Рассмотрим несколько практических задач, в которых можно использовать периметр прямоугольного треугольника.
1. Расчет площади прямоугольного треугольника:
Площадь прямоугольного треугольника можно вычислить путем умножения половины произведения его катетов на высоту:
S = (a * b) / 2, где a и b - катеты треугольника.
Для вычисления площади треугольника, часто требуется знать его периметр. При расчетах полупериметра треугольника используют следующую формулу:
S = √(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника.
2. Построение забора:
Если требуется оградить прямоугольный участок забором, то для определения его длины необходимо вычислить периметр прямоугольного треугольника, образуемого сторонами участка. Для этого сложите длины всех сторон треугольника:
| Сторона | Длина |
|---|---|
| Катет a | a |
| Катет b | b |
| Гипотенуза c | c |
Полученное значение периметра позволит определить длину забора, необходимого для ограждения участка.
3. Расчет длины трассы:
Если известны длины двух катетов треугольника, можно определить длину трассы, пройденной по гипотенузе данного треугольника. Для этого необходимо сложить длины всех сторон:
| Сторона | Длина |
|---|---|
| Катет a | a |
| Катет b | b |
| Гипотенуза c | c |
Полученное значение периметра будет давать общую длину пройденной трассы.
В практических задачах периметр прямоугольного треугольника используется для различных расчетов и измерений. Он позволяет определить не только длину ограждающего контура и трассы, но и площадь треугольника. Зная периметр и другие параметры треугольника, можно решать разнообразные задачи, связанные с его геометрией и применением в повседневной жизни.
Ограничения и известные оговорки при использовании формулы для нахождения периметра прямоугольного треугольника

При использовании формулы для нахождения периметра прямоугольного треугольника важно учитывать некоторые ограничения и известные оговорки. Эти факторы могут влиять на точность результата и требуют особого внимания при решении задачи.
- Корректность измерений: Для точного определения периметра прямоугольного треугольника необходимо, чтобы измерения катетов были сделаны с высокой точностью, используя подходящие инструменты. Небольшие ошибки в измерениях могут привести к значительной погрешности в результате.
- Правильность выбора формулы: Существует несколько формул, которые могут быть использованы для нахождения периметра прямоугольного треугольника, включая фундаментальную формулу Пифагора. Важно выбрать правильную формулу, соответствующую данным задачи.
- Проверка условий: Для применения формулы для нахождения периметра прямоугольного треугольника необходимо убедиться, что заданные стороны действительно являются катетами прямоугольного треугольника. Это можно сделать, проверив, удовлетворяют ли заданные стороны условию Пифагора: a^2 + b^2 = c^2, где a и b - катеты, c - гипотенуза.
- Нравственность использования: При использовании формулы для нахождения периметра прямоугольного треугольника необходимо помнить, что эта информация может применяться как для полезных, так и для вредных целей. Важно использовать полученный результат с умом и этически.
Учитывая эти ограничения и известные оговорки, можно с уверенностью использовать формулу для нахождения периметра прямоугольного треугольника и получить достоверные результаты при решении соответствующих задач.
Интересные факты о периметре прямоугольного треугольника
1. Сумма длин катетов всегда будет меньше, чем сумма длин гипотенузы и одного из катетов. Это связано с тем, что гипотенуза всегда является наибольшей стороной прямоугольного треугольника.
2. Периметр прямоугольного треугольника можно выразить через его катеты и гипотенузу с помощью формулы: периметр = катет 1 + катет 2 + гипотенуза.
3. В периметре прямоугольного треугольника присутствует отношение Пифагора, которое гласит, что квадрат длины гипотенузы равен сумме квадратов длин катетов: гипотенуза^2 = катет 1^2 + катет 2^2.
4. Каждый прямоугольный треугольник имеет свой уникальный периметр, который можно вычислить по его сторонам. Это позволяет использовать периметр для идентификации и классификации прямоугольных треугольников.
5. Периметр прямоугольного треугольника является положительной величиной и всегда больше нуля. Это связано с тем, что длина каждой стороны треугольника не может быть отрицательной.
Изучение периметра прямоугольного треугольника помогает нам лучше понять его особенности и свойства. Это важная тема в геометрии, которая находит применение в различных областях науки и практики.