Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой. Одним из способов нахождения периметра такого треугольника является использование высоты треугольника. Высота – это отрезок, проведенный из вершины треугольника до противоположной стороны и перпендикулярный этой стороне.
Чтобы найти периметр равнобедренного треугольника по высоте, нужно знать высоту (h) и любую сторону треугольника (a). Тогда можно воспользоваться следующей формулой:
P = 2a + h,
где P обозначает периметр, а a и h – длины стороны и высоты треугольника соответственно.
Теперь, когда у вас есть формула, вы можете легко найти периметр равнобедренного треугольника по его высоте. Просто введите известные значения стороны и высоты в формулу, выполните вычисления и получите ответ. Не забывайте, что значения стороны и высоты должны быть в одной и той же системе измерения (например, сантиметры или метры).
Роль периметра в геометрии

Периметр имеет несколько важных свойств:
| 1 | Периметр позволяет измерить длину фигуры и сравнить ее с другими геометрическими объектами. Это очень полезно при сравнении размеров, планировании и построении различных объектов. |
| 2 | Периметр также может быть использован для нахождения площади фигуры. Например, для прямоугольника периметр и площадь связаны следующим образом: площадь равна произведению двух сторон, а периметр – удвоенной сумме этих сторон. |
| 3 | Периметр также играет важную роль в изучении свойств фигур, таких как равенство сторон и углов. Например, в равнобедренном треугольнике периметр можно выразить через длину одной из сторон и основание треугольника, используя формулу. |
В целом, периметр является одной из основных характеристик геометрических фигур и позволяет проводить различные измерения и сравнения, а также является важным инструментом для решения задач в геометрии.
Что такое равнобедренный треугольник
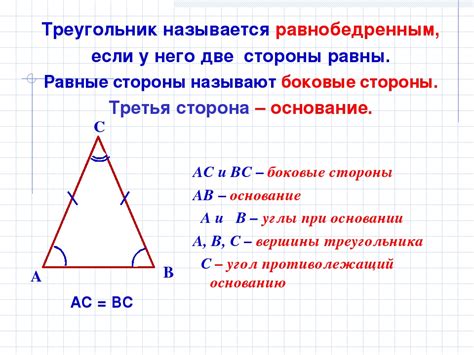
Свойства равнобедренного треугольника позволяют нам решать различные задачи, такие как нахождение периметра, площади, высоты и других величин. Одним из важных свойств равнобедренного треугольника является нахождение высоты, которая проходит через вершину треугольника и опускается на противоположную сторону.
Найти периметр равнобедренного треугольника по высоте можно при помощи формулы:
- Вычислите основание треугольника (сторону, на которую опущена высота).
- Вычислите длину других двух сторон треугольника (равных между собой).
- Сложите длины всех трех сторон, чтобы получить периметр равнобедренного треугольника.
Зная высоту равнобедренного треугольника, мы можем использовать данную формулу для нахождения периметра этого треугольника.
Как определить высоту равнобедренного треугольника
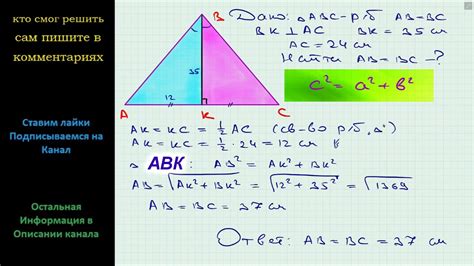
Существует несколько способов определить высоту равнобедренного треугольника:
- Использование формулы, связывающей основание, высоту и площадь треугольника.
- Применение теоремы Пифагора для нахождения высоты при известных сторонах треугольника.
- Использование свойств подобных треугольников для определения высоты по известной длине основания и соответствующей стороне.
Выбранный метод определения высоты зависит от доступных данных и требуемой точности вычислений.
Таким образом, высота равнобедренного треугольника может быть вычислена различными способами, и выбор метода зависит от задачи и доступных данных.
Значение периметра равнобедренного треугольника
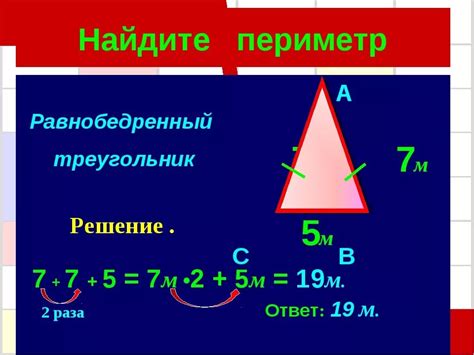
Периметр равнобедренного треугольника определяется как сумма длин всех его сторон. В случае равнобедренного треугольника с основанием, высота которого известна, можно использовать специальную формулу для нахождения периметра.
Пусть a - длина основания треугольника, а h - его высота. Равнобедренный треугольник будет иметь две равные стороны и одну основание. Из определения высоты равнобедренного треугольника следует, что высота является биссектрисой угла между равными сторонами.
Для нахождения периметра равнобедренного треугольника по высоте, можно воспользоваться следующей формулой:
P = 2a + b
Где P - периметр треугольника, a - длина основания, b - длина боковой стороны равнобедренного треугольника.
Таким образом, чтобы найти периметр равнобедренного треугольника по известной высоте, нужно умножить длину основания на 2 и добавить длину одной из боковых сторон.
Формула для расчета периметра по высоте
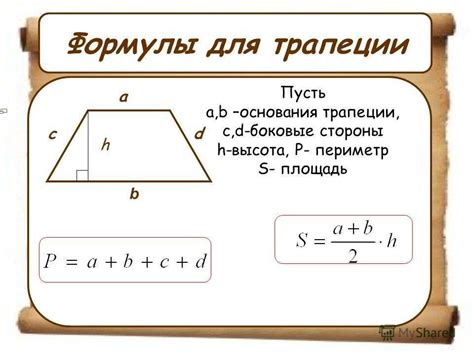
При расчете периметра равнобедренного треугольника по известной высоте можно использовать следующую формулу:
Периметр = 2 * a + b, где
- a - длина основания треугольника
- b - длина боковой стороны треугольника
Для вычисления периметра необходимо знать длину основания и боковой стороны. Однако, если известно только значение высоты треугольника, можно использовать другую формулу:
Периметр = 2 * (sqrt((h^2) + (b/2)^2)) + b, где
- h - высота треугольника
- b - длина боковой стороны треугольника
Эта формула основана на теореме Пифагора, которая позволяет найти длину гипотенузы прямоугольного треугольника по длинам его катетов.
При использовании данной формулы необходимо знать значение высоты и длину боковой стороны равнобедренного треугольника. В результате вычислений получится периметр треугольника.
Практические советы для нахождения периметра

Нахождение периметра равнобедренного треугольника по высоте может быть достаточно простым, если следовать нескольким практическим советам:
1. Определите высоту треугольника:
Перед тем как начать находить периметр треугольника, важно установить значение его высоты. Высота является вертикальной линией, проходящей через вершину треугольника и перпендикулярной его основанию. Если известна только высота, можно применить формулу для нахождения периметра.
2. Используйте формулу для периметра треугольника:
Если дана высота треугольника, то периметр может быть найден по формуле: периметр = основание + (2 * сторона). Основание треугольника - это одна из его сторон, как правило, самая длинная из них. В случае равнобедренного треугольника, другие две стороны будут равны между собой.
3. Измерьте стороны треугольника:
Перед расчетом периметра, измерьте длину каждой из сторон треугольника с помощью линейки или другого измерительного инструмента. Запишите полученные значения, чтобы использовать их в формуле для периметра.
4. Подставьте значения в формулу:
Обратитесь к формуле периметра и подставьте измеренные значения в соответствующие переменные. Основание треугольника будет соответствовать его самой длинной стороне, а сторона будет равна двум другим сторонам, так как треугольник равнобедренный.
5. Вычислите периметр:
После подстановки значений в формулу, выполните необходимые вычисления, чтобы найти значение периметра. Пример: если основание треугольника равно 5 см, а стороны равны 3 см каждая, то периметр будет равен: периметр = 5 + (2 * 3) = 11 см.
Следуя этим практическим советам, можно легко найти периметр равнобедренного треугольника по его высоте. Не забывайте, что периметр - это сумма длин всех сторон треугольника.
Примеры вычисления периметра равнобедренного треугольника
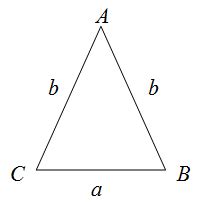
Пример 1: Пусть у нас есть равнобедренный треугольник, у которого сторона равна 6 см, а основание равно 8 см. Чтобы найти периметр треугольника, мы можем использовать следующую формулу:
Периметр = сторона + сторона + основание
Заменяя значения в формуле, получаем:
Периметр = 6 см + 6 см + 8 см = 20 см
Таким образом, периметр этого треугольника равен 20 см.
Пример 2: Рассмотрим равнобедренный треугольник, у которого сторона равна 5 м и основание равно 7 м. Используем формулу для вычисления периметра:
Периметр = сторона + сторона + основание
Подставим значения в формулу:
Периметр = 5 м + 5 м + 7 м = 17 м
Таким образом, периметр равнобедренного треугольника составляет 17 м.