Периметр равнобедренного треугольника является одним из важных показателей, который помогает определить длину его сторон. Он может быть вычислен различными способами с использованием различных формул и методов. В этой статье мы рассмотрим несколько способов нахождения периметра равнобедренного треугольника и расскажем о соответствующих формулах.
Равнобедренный треугольник - это треугольник, у которого две стороны имеют одинаковую длину. Такой треугольник часто встречается в геометрии и имеет некоторые особенности, которые мы будем учитывать при нахождении его периметра.
Первый способ вычисления периметра равнобедренного треугольника основывается на его определении. Периметр треугольника - это сумма длин всех его сторон. В случае равнобедренного треугольника, у которого сторона АВ равна стороне АС, периметр можно выразить следующей формулой:
Периметр = АВ + АС + ВС
Здесь АВ и АС - стороны треугольника, а ВС - его основание.
Также существует и другой способ нахождения периметра равнобедренного треугольника. Если известна длина стороны АВ и основания ВС, то периметр можно вычислить по следующей формуле:
Периметр = 2 * АВ + ВС
В этой формуле длина стороны АВ учитывается дважды, так как равнобедренный треугольник содержит две одинаковы стороны.
Таким образом, нахождение периметра равнобедренного треугольника достаточно просто, если известны значения его сторон или основания. Это может быть особенно полезно в различных задачах и упражнениях из геометрии и математики.
Определение равнобедренного треугольника
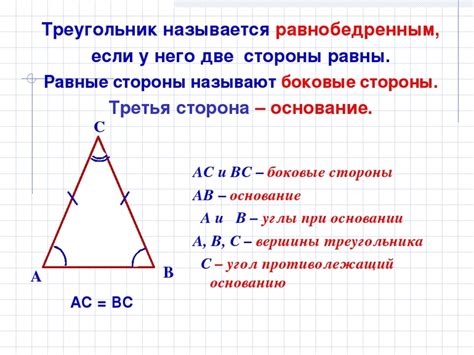
Равнобедренным треугольником называется треугольник, у которого две стороны и два угла равны между собой. Такие стороны называются боковыми сторонами, а вершина, из которой они исходят, называется вершиной угла. Равнобедренный треугольник обладает особыми свойствами, которые позволяют определить его периметр с помощью специальных формул.
В равнобедренном треугольнике две из трех сторон равны. Периметр такого треугольника можно найти, сложив длины всех его сторон. Однако существуют и более простые формулы для расчета периметра.
Если сторона треугольника равна a, то его периметр равен 2a + c, где c - длина основания треугольника. Однако, если известны все три стороны треугольника, то периметр можно вычислить непосредственно по формуле: a + b + c, где a и b - равные стороны, а c - основание треугольника.
Определение геометрической фигуры
Геометрические фигуры могут иметь различные формы и размеры. Они могут быть классифицированы по своим характеристикам, таким как количество сторон, углов, длин сторон и радиусов.
Некоторые из наиболее распространенных геометрических фигур включают треугольники, квадраты, прямоугольники, круги, овалы и многоугольники. Они играют важную роль в геометрии и используются в различных областях, включая архитектуру, строительство, инженерию и дизайн.
Для каждой геометрической фигуры существуют определенные способы ее измерения и вычисления, такие как нахождение площади, периметра и объема. Также важно знать характеристики каждой фигуры, чтобы правильно использовать их в решении математических задач и построении конструкций.
Изучение геометрических фигур позволяет развивать пространственное мышление, аналитические и логические навыки, а также способность абстрагироваться и находить решения сложных задач.
Особенности равнобедренного треугольника
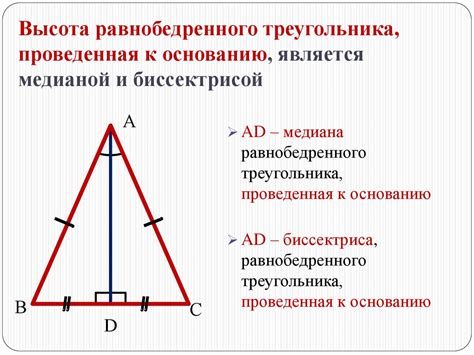
- У равнобедренного треугольника две равные стороны, называемые равными боковыми сторонами. Третья сторона называется основанием.
- Углы при основании равнобедренного треугольника также равны.
- Углы при вершине равнобедренного треугольника всегда равны друг другу и равны половине суммы углов при основании.
- Перпендикуляр, проведенный из вершины равнобедренного треугольника к основанию, делит его на два равных прямоугольных треугольника.
Как найти периметр равнобедренного треугольника
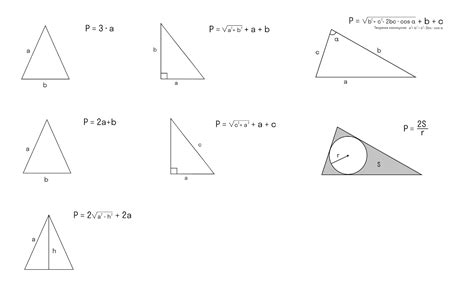
Существует несколько способов найти периметр равнобедренного треугольника:
| Метод | Формула |
|---|---|
| Использование длин сторон | Периметр = AB + AC + BC |
| Использование длин основания и высоты | Периметр = 2 * (OS + SS), где OS - основание треугольника, SS - сторона треугольника |
| Использование угла | Периметр = 2 * BC * cos(0.5 * угол ABC), где BC - сторона треугольника, угол ABC - угол при вершине A |
Следует отметить, что для использования последней формулы необходимо знать значение угла при вершине A.
Выбор метода зависит от того, какая информация у нас есть о треугольнике. Если известны длины сторон, можно использовать первый метод. Если известны длина основания и высота, можно использовать второй метод. Если известна только сторона и угол, можно использовать третий метод.
Изучение этих методов позволяет легко находить периметр равнобедренного треугольника в зависимости от предоставленной информации о треугольнике.
Метод 1: Использование длин сторон треугольника
Периметр равнобедренного треугольника можно найти с использованием длин его сторон. Рассмотрим треугольник, у которого две стороны равны между собой, а третья сторона отличается.
Пусть длина равных сторон равна a, а длина третьей стороны равна b. Чтобы найти периметр треугольника, нужно сложить длины всех его сторон: P = a + a + b = 2a + b.
Таким образом, для нахождения периметра равнобедренного треугольника достаточно знать длину двух его сторон и длину третьей стороны.
Метод 2: Использование формулы
Для нахождения периметра равнобедренного треугольника можно использовать следующую формулу:
- Найдите длину основания треугольника. Оно является одной из сторон, которая не является равной стороне треугольника.
- Найдите длину боковой стороны треугольника. Она является равной стороной треугольника.
- Умножьте длину основания на 2 и прибавьте к нему длину боковой стороны. Полученная сумма будет периметром равнобедренного треугольника.
Например, пусть основание треугольника равно 2 см, а боковая сторона равна 4 см. Следуя формуле, умножим 2 на 2 и прибавим 4. Получим, что периметр равнобедренного треугольника равен 8 см.
Используя формулу, можно находить периметр равнобедренных треугольников с любыми заданными сторонами.