Тетраэдр - одно из простейших тел в трехмерном пространстве, состоящее из четырех треугольных граней. Это фигура, которая часто встречается в геометрии и инженерии. Когда мы работаем с тетраэдром, иногда возникает необходимость найти периметр его сечения. Прежде чем мы рассмотрим, как это сделать, давайте вспомним некоторые основные понятия.
Периметр - это длина замкнутой кривой, охватывающей границу плоской фигуры. То есть, если мы возьмем линейку и измерим длины всех сторон фигуры, а затем сложим эти значения, мы получим периметр.
Сразу стоит отметить, что сечение тетраэдра образует многогранник, и его периметр можно найти по тем же принципам, что и для других многогранников. Давайте рассмотрим пример, чтобы увидеть, как это работает.
Определение понятия "периметр сечения тетраэдра"
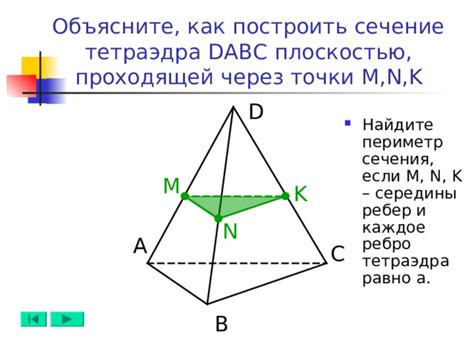
Для определения периметра сечения тетраэдра необходимо знать длины всех сторон этого тетраэдра и угол, под которым плоскость пересекает грани. Если известны только длины некоторых сторон и углы, то требуется использовать соответствующие геометрические формулы для нахождения неизвестных величин.
Понятие "периметр сечения тетраэдра" имеет важное значение в геометрии и инженерных расчетах. Оно позволяет определить длину кривой линии внутри тетраэдра, которая может быть использована для различных математических и инженерных приложений.
Значение известных ребер при нахождении периметра сечения
При нахождении периметра сечения тетраэдра из известных ребер необходимо учитывать их длину и взаимное положение. Ребра тетраэдра могут быть различной длины и могут находиться в разных плоскостях, поэтому важно правильно определить и использовать их значения.
Периметр сечения тетраэдра представляет собой сумму длин всех ребер, которые пересекаются с плоскостью, заданной сечением. Известные ребра тетраэдра могут быть одновременно частями периметра сечения и периметра других плоскостей.
| Справочная информация | Описание |
|---|---|
| Ребро тетраэдра | Сторона тетраэдра, которая соединяет две вершины |
| Периметр сечения | Сумма длин всех ребер, пересекающих плоскость сечения |
| Плоскость сечения | Плоская фигура, полученная пересечением тетраэдра и плоскости |
Способы нахождения периметра сечения тетраэдра
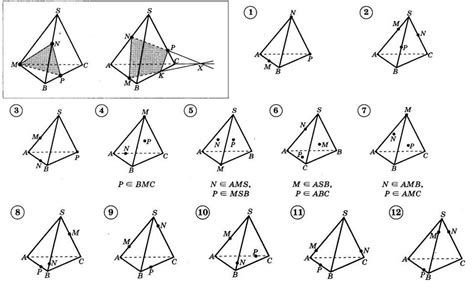
Периметр сечения тетраэдра можно найти с помощью различных методов, в зависимости от того, какие данные о тетраэдре у нас имеются. Рассмотрим несколько способов.
1. Известны все ребра сечения
Если нам известны все ребра сечения, то для нахождения периметра необходимо сложить длины всех ребер сечения.
2. Известны длины трех ребер сечения
Если нам известны длины трех ребер сечения, то для нахождения периметра можно использовать формулу трех сторон треугольника.
| Ребро 1 | Ребро 2 | Ребро 3 | Периметр |
|---|---|---|---|
| a | b | c | a + b + c |
3. Известны длины двух ребер сечения и угол между ними
Если нам известны длины двух ребер сечения и угол между ними, то для нахождения периметра можно использовать теорему косинусов.
| Ребро 1 | Ребро 2 | Угол между ребрами | Периметр |
|---|---|---|---|
| a | b | α | a + b + 2√(a*b*cos(α/2)) |
Это лишь несколько способов нахождения периметра сечения тетраэдра. В зависимости от предоставленных данных, можно использовать различные формулы и методы для решения данной задачи.
Пример нахождения периметра сечения тетраэдра из известных ребер
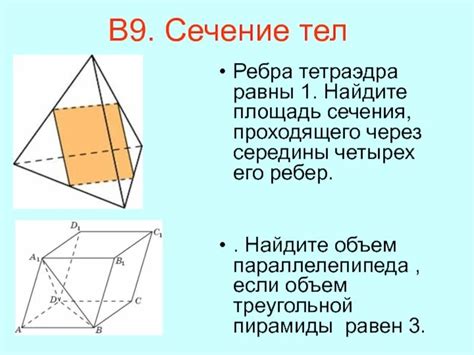
Для нахождения периметра сечения тетраэдра из известных ребер необходимо использовать геометрические и математические принципы. Для примера рассмотрим тетраэдр, у которого известны следующие ребра: a, b, c и d.
Периметр сечения тетраэдра может быть найден путем сложения длин всех ребер сечения. Сначала определяем точки пересечения ребер тетраэдра для формирования плоскости сечения. Затем, используя известные ребра, находим длины всех ребер сечения, а их сумма и будет периметром сечения тетраэдра.
Пример расчета периметра сечения:
Дано:
- Длина ребра a = 4
- Длина ребра b = 5
- Длина ребра c = 6
- Длина ребра d = 7
Сначала находим точки пересечения ребер тетраэдра и формируем плоскость сечения. Для удобства рассмотрим пересечение ребер a и b в точке A, ребер b и c в точке B, ребер c и d в точке C, и ребер d и a в точке D. Таким образом, плоскость сечения образуется.
Далее вычисляем длины ребер сечения, используя теорему Пифагора и расстояние между двуми точками:
- Длина ребра сечения AB = √((a + b)^2 - (|a - b|/2)^2)
- Длина ребра сечения BC = √((b + c)^2 - (|b - c|/2)^2)
- Длина ребра сечения CD = √((c + d)^2 - (|c - d|/2)^2)
- Длина ребра сечения DA = √((d + a)^2 - (|d - a|/2)^2)
Для данного примера:Длина ребра сечения AB = √((4 + 5)^2 - (|4 - 5|/2)^2) = √(81 - 0.25) = √80.75 ≈ 8.99
Длина ребра сечения BC = √((5 + 6)^2 - (|5 - 6|/2)^2) = √(121 - 0.25) = √120.75 ≈ 10.98
Длина ребра сечения CD = √((6 + 7)^2 - (|6 - 7|/2)^2) = √(169 - 0.25) = √168.75 ≈ 12.99
Длина ребра сечения DA = √((7 + 4)^2 - (|7 - 4|/2)^2) = √(121 - 3.375) = √117.625 ≈ 10.85
Наконец, суммируем все длины ребер сечения, чтобы найти периметр сечения:
Периметр сечения = AB + BC + CD + DA ≈ 8.99 + 10.98 + 12.99 + 10.85 ≈ 43.81
Таким образом, периметр сечения тетраэдра, состоящего из известных ребер a, b, c и d, равен приблизительно 43.81.
Возможные сложности при нахождении периметра сечения тетраэдра
Найдение периметра сечения тетраэдра может быть достаточно сложной задачей из-за ряда факторов.
Во-первых, необходимо иметь точные измерения ребер тетраэдра. В реальной жизни это может быть нетривиальной задачей, особенно при работе с реальными объектами, где могут присутствовать неточности и погрешности в измерениях.
Во-вторых, сам процесс нахождения периметра сечения требует математических расчетов. Для этого необходимо знание соответствующих математических формул и умение правильно применять их. Это может быть сложно для людей, которые не имеют достаточного опыта или знаний в области математики.
Еще одной сложностью может быть необходимость разбивать тетраэдр на более простые фигуры, например, треугольники или параллелограммы, для того чтобы рассчитать периметр сечения. Это может быть трудоемким процессом и требовать дополнительных математических навыков.
Также следует отметить, что периметр сечения тетраэдра может быть разным в зависимости от выбранного сечения. Это означает, что можно получить разные результаты при выборе различных плоскостей для сечения тетраэдра. Поэтому необходимо быть внимательным и аккуратным при выборе и расчете сечения.
В целом, нахождение периметра сечения тетраэдра может быть сложной задачей, требующей точных измерений, математических расчетов и умения работать с геометрическими фигурами.
Важность понимания периметра сечения тетраэдра в математике и технике
Понимание периметра сечения тетраэдра имеет большое значение в математике, так как позволяет решать различные геометрические задачи и изучать свойства тетраэдра. Зная периметр сечения, можно вычислить его площадь и объем, а также провести различные анализы и исследования.
В технике понимание периметра сечения тетраэдра также играет важную роль. Например, в архитектуре и инженерии, при проектировании и строительстве зданий и сооружений, знание периметра сечения позволяет определить оптимальные размеры и форму элементов конструкции, а также прогнозировать поведение системы в различных условиях.
Кроме того, понимание периметра сечения тетраэдра может быть полезно в разработке компьютерной графики и визуализации данных. Зная периметр сечения, можно точно отобразить его на экране, создавая трехмерные модели и компьютерные симуляции.