Периметр треугольника - это сумма длин его сторон. Этот параметр является одним из основных характеристик треугольника. Зная площадь треугольника, иногда бывает полезно узнать его периметр. Наша статья поможет вам найти периметр треугольника с известной площадью.
Первым шагом для нахождения периметра треугольника с известной площадью является использование формулы для вычисления площади треугольника. Формула для нахождения площади треугольника равна половине произведения длины основания треугольника на высоту. Основание - это одна из сторон треугольника, а высота - это перпендикуляр из вершины треугольника к основанию.
Далее необходимо использовать полученное значение площади и формулы для нахождения периметра треугольника. Для треугольника, у которого известна площадь, периметр можно выразить через длины его сторон и радиус описанной окружности. Формула выглядит так: Периметр = 2 * радиус описанной окружности * sin(α/2) + 2 * радиус описанной окружности * sin(β/2) + 2 * радиус описанной окружности * sin(γ/2), где α, β, γ - углы треугольника. Для нахождения периметра треугольника с известной площадью необходимо решить эту формулу относительно периметра и подставить значение площади.
Периметр треугольника и его площадь: как найти связь между ними?
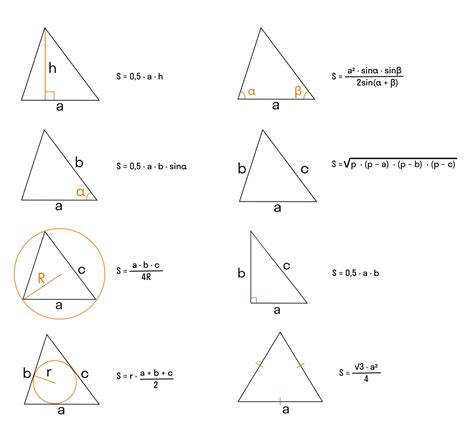
Периметр треугольника – это сумма длин всех его сторон. Для нахождения периметра треугольника необходимо сложить длины всех его сторон. Эта характеристика позволяет оценить общую длину замкнутой линии, образующей треугольник.
Площадь треугольника – это мера его плоскости. Для нахождения площади нужно использовать базовую формулу для треугольника – "половина произведения основания на высоту". Основание треугольника – это одна из его сторон, а высота – перпендикуляр, опущенный из вершины треугольника на основание.
Существует связь между периметром и площадью треугольника. В самом деле, периметр треугольника зависит от длин его сторон, а длина сторон влияет на площадь треугольника.
Например, если мы увеличим длины сторон треугольника, его периметр также увеличится, а площадь может измениться, в зависимости от других факторов. Если мы уменьшим длины сторон, периметр уменьшится и площадь также может измениться.
Таким образом, можно сказать, что периметр и площадь треугольника связаны, но при изменении одной из этих характеристик другая может измениться или остаться постоянной. Это зависит от различных факторов, таких как форма и размеры треугольника.
Итак, периметр и площадь треугольника имеют связь, которая зависит от длины его сторон и других факторов. Понимание этой связи поможет вам лучше понять геометрические свойства треугольника и использовать их в практике.
Метод 1: воспользуйтесь формулой Герона!
Для вычисления периметра треугольника, когда известна его площадь, можно использовать формулу Герона.
Формула Герона позволяет вычислить площадь треугольника по длинам его сторон. Если известна площадь треугольника и одна из его сторон, то можно найти оставшиеся две стороны с помощью формулы Герона.
Для применения этого метода нужно следовать таким шагам:
- Найти длину одной из сторон треугольника.
- Найти площадь треугольника при помощи известных длин сторон.
- Пересчитать стороны треугольника, используя полученные значения площади и известную сторону.
- Вычислить периметр треугольника, сложив длины всех его сторон.
Этот метод основан на использовании формулы Герона и позволяет найти периметр треугольника, когда известна его площадь и одна из сторон. Он может быть полезен при решении задач, связанных с измерением и вычислением периметра треугольников.
Метод 2: использование значений сторон треугольника!
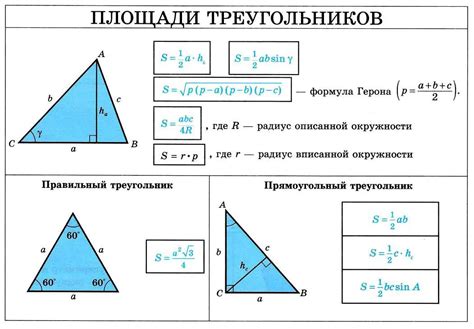
Если известны значения сторон треугольника, можно использовать их для вычисления его периметра. Обозначим стороны треугольника как a, b и c. Периметр треугольника вычисляется по формуле:
Периметр = a + b + c
Этот метод особенно полезен, если известны все три стороны треугольника. В этом случае, достаточно просто сложить значения сторон для получения периметра.
Пример:
Пусть дан треугольник со сторонами a = 5 см, b = 7 см и c = 9 см. Чтобы найти периметр треугольника, сложим значения сторон: Периметр = 5 см + 7 см + 9 см = 21 см.
Таким образом, периметр треугольника со сторонами a = 5 см, b = 7 см и c = 9 см равен 21 см.