Периметр треугольника - это сумма длин всех его сторон. Расчет периметра треугольника с десятичными дробями может быть сложнее, чем с целыми числами, но с правильными методами и примерами вы сможете легко справиться с этой задачей.
Для начала нужно знать длины всех сторон треугольника. Если известны десятичные дроби, то можно использовать их точные значения при расчете. Например, если сторона треугольника равна 3.25 единицам, то эту цифру можно использовать в вычислениях без округления.
Чтобы найти периметр треугольника, нужно сложить длины всех его сторон. Можно использовать формулу:
Периметр = сторона A + сторона B + сторона C
Давайте рассмотрим пример: у нас есть треугольник со сторонами 2.5, 3.75 и 4.25. Чтобы найти его периметр, нужно сложить все стороны: 2.5 + 3.75 + 4.25 = 10.5. Итак, периметр треугольника равен 10.5 единицам.
Методы вычисления периметра треугольника с десятичными дробями
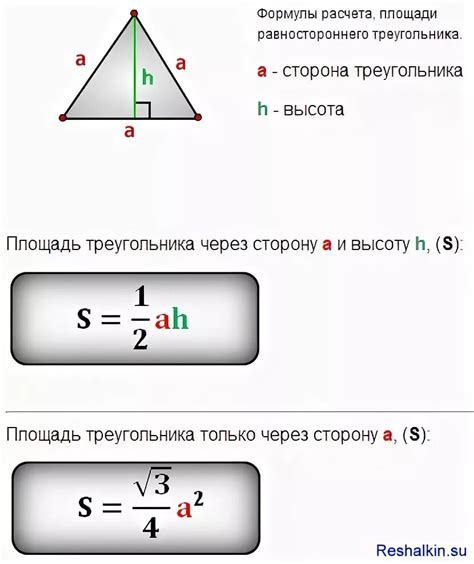
1. Метод сложения длин сторон:
- Измерьте длину каждой стороны треугольника с помощью линейки или другого измерительного инструмента.
- Сложите все измеренные значения вместе, чтобы получить периметр треугольника.
2. Метод использования координат точек:
- Запишите координаты каждой точки треугольника (x1, y1), (x2, y2) и (x3, y3).
- Вычислите расстояния между каждой парой точек треугольника, используя формулу расстояния между двумя точками.
- Сложите все полученные расстояния, чтобы получить периметр треугольника.
3. Метод использования полупериметра:
- Измерьте длину каждой стороны треугольника с помощью линейки или другого измерительного инструмента.
- Рассчитайте полупериметр треугольника, который равен сумме длин всех сторон, поделенной на 2.
- Умножьте полупериметр на 2, чтобы получить периметр треугольника.
Зная методы вычисления периметра треугольника с десятичными дробями, вы сможете легко определить его длину и использовать эту информацию для решения различных геометрических задач.
Формула полупериметра и длин сторон треугольника
p = (a + b + c) / 2
где a, b и c - длины сторон треугольника.
После нахождения полупериметра, периметр треугольника можно вычислить, умножив полупериметр на 2.
Длины сторон треугольника представляют собой отрезки, соединяющие вершины треугольника. Для нахождения периметра треугольника необходимо знать значения длин всех трех сторон, обозначенных как a, b и c. Для измерения длин сторон можно использовать линейку или другой измерительный инструмент. В случае, когда сторона задана в виде десятичной дроби, необходимо быть внимательным и точно измерить ее длину.
Использование координат вершин треугольника
Для нахождения периметра треугольника с десятичными дробями можно использовать координаты его вершин.
Координаты вершин треугольника задаются в виде упорядоченных пар чисел (x, y), где x - это горизонтальное расстояние от начала координат до вершины, а y - вертикальное расстояние.
Пусть треугольник имеет вершины A(x1, y1), B(x2, y2) и C(x3, y3). Тогда его периметр можно найти с помощью формулы:
Периметр = AB + BC + AC
AB = √((x2 - x1)² + (y2 - y1)²)
BC = √((x3 - x2)² + (y3 - y2)²)
AC = √((x3 - x1)² + (y3 - y1)²)
Зная значения координат вершин треугольника, подставляем их в формулу и находим периметр.
Пример:
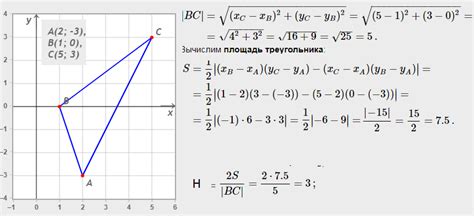
Дан треугольник со следующими координатами вершин:
A(1.5, 2)
B(4.8, 5.2)
C(7.2, 3.1)
Вычислим периметр треугольника:
AB = √((4.8 - 1.5)² + (5.2 - 2)²) ≈ √(3.3² + 3.2²) ≈ √(10.89 + 10.24) ≈ √21.13 ≈ 4.60
BC = √((7.2 - 4.8)² + (3.1 - 5.2)²) ≈ √(2.4² + (-2.1)²) ≈ √(5.76 + 4.41) ≈ √10.17 ≈ 3.19
AC = √((7.2 - 1.5)² + (3.1 - 2)²) ≈ √(5.7² + 1.1²) ≈ √(32.49 + 1.21) ≈ √33.70 ≈ 5.81
Периметр треугольника равен AB + BC + AC ≈ 4.60 + 3.19 + 5.81 ≈ 13.60.
Таким образом, периметр треугольника с заданными координатами вершин равен приблизительно 13.60.
Примеры вычисления периметра треугольника с десятичными дробями

Давайте рассмотрим несколько примеров вычисления периметра треугольника с десятичными дробями.
Пример 1:
Пусть у нас есть треугольник ABC, где стороны AB, BC и AC равны 2.5, 3.8 и 4.2 соответственно. Чтобы найти периметр треугольника, нужно сложить длины всех его сторон: 2.5 + 3.8 + 4.2 = 10.5. Поэтому периметр треугольника ABC равен 10.5.
Пример 2:
Рассмотрим треугольник XYZ, стороны которого равны 1.7, 2.4 и 3.1. Складывая эти значения, получаем: 1.7 + 2.4 + 3.1 = 7.2. Таким образом, периметр треугольника XYZ составляет 7.2.
Пример 3:
Пусть треугольник PQR имеет стороны длиной 3.9, 5.6 и 2.1. Путем сложения данных значений мы получаем: 3.9 + 5.6 + 2.1 = 11.6. Таким образом, периметр треугольника PQR равен 11.6.
Используя эти примеры, мы можем легко вычислять периметр треугольника с десятичными дробями, сложив длины всех его сторон. Важно помнить, что при работе с десятичными дробями следует быть внимательным и точность вычислений должна быть сохранена.