Решение математических задач на нахождение первообразной функции является важной задачей в области математического анализа. Одним из способов решения этой задачи является использование точек на графике функции. В данной статье мы рассмотрим метод нахождения первообразной функции через точку М на графике.
Первообразная функция является обратной операцией к дифференцированию функции. Если для заданной функции f(x) мы знаем ее производную F'(x), то нахождение первообразной функции F(x) заключается в нахождении такой функции, производная которой равна f(x).
Использование точки М на графике функции позволяет упростить процесс нахождения первообразной функции. Пусть точка М(x, y) лежит на графике функции f(x). Тогда мы можем записать уравнение производной функции F'(x) как F'(x) = y. Таким образом, нахождение первообразной функции F(x), проходящей через точку М, сводится к решению уравнения F'(x) = y.
Определение первообразной функции
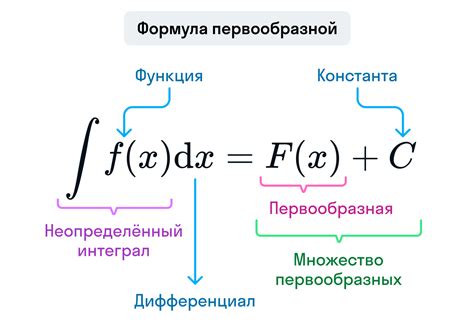
Другими словами, первообразная функция F(x) для функции f(x) – это такая функция, производная которой равна f(x). Иногда первообразную функцию также называют антипроизводной функцией.
Для определения первообразной функции можно использовать методы интегрирования, которые позволяют находить антипроизводные функции.
Первообразные функции имеют некоторые свойства, которые могут быть использованы для нахождения их значений. Например, первообразная функция может иметь неопределенный интеграл, обозначаемый символом ✳. Кроме того, первообразные функции обладают свойством линейности, что означает, что сумма или разность двух первообразных функций также является первообразной функцией.
Знание первообразной функции позволяет нам находить значение функции в произвольной точке, зная только значение функции и ее производной в некоторой точке – начальной точке. Таким образом, определение первообразной функции является важным инструментом в математическом анализе и является основополагающим понятием при решении дифференциального уравнения.
Интеграл функции и его свойства

Для функции f(x), интеграл от этой функции на заданном интервале [a, b] обозначается как ∫abf(x)dx. Интеграл представляет собой определенный интеграл, так как он имеет конкретные пределы интегрирования a и b.
Свойства интеграла:
- Линейность. Интеграл линеен, то есть сумма интегралов функций равна интегралу от суммы функций. Формально это записывается как ∫ab(f(x) + g(x))dx = ∫abf(x)dx + ∫abg(x)dx.
- Аддитивность. Если интервал интегрирования разбивается на два подынтервала, то интеграл от функции на всем интервале равен сумме интегралов от функции на подынтервалах. Формально это записывается как ∫abf(x)dx = ∫acf(x)dx + ∫cbf(x)dx.
- Интеграл от постоянной функции. Интеграл от постоянной функции равен произведению постоянной функции на разность пределов интегрирования. Формально это записывается как ∫abkdx = k(b-a), где k – постоянная.
- Интеграл от суммы двух функций. Интеграл от суммы двух функций равен сумме интегралов от каждой из функций. Формально это записывается как ∫ab(f(x) + g(x))dx = ∫abf(x)dx + ∫abg(x)dx.
Использование свойств интеграла позволяет упростить вычисления и находить первообразные функции с помощью интегрирования.
Первообразная функции и ее определение
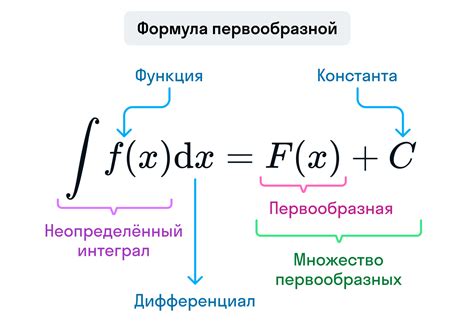
Первообразная функции может отличаться от исходной функции на константу, поэтому в общем виде она записывается в виде F(x) + C, где C – произвольная постоянная.
Нахождение первообразной функции может быть полезным при решении задач в физике, экономике и других науках, а также в решении неопределенных интегралов. Зная первообразную функцию, мы можем найти определенный интеграл, который позволяет найти площадь под графиком функции.
Существует множество методов и техник для нахождения первообразной функции, таких как метод подстановки, интегрирование по частям, интегрирование дробно-рациональной функции и др. Каждый метод имеет свои особенности и применяется в зависимости от вида исходной функции.
Интегрирование является обратной операцией к дифференцированию и позволяет нам найти первообразную функции. Однако не все функции имеют элементарные первообразные, и в таких случаях используются численные методы для решения интегралов.
Точка М на графике функции
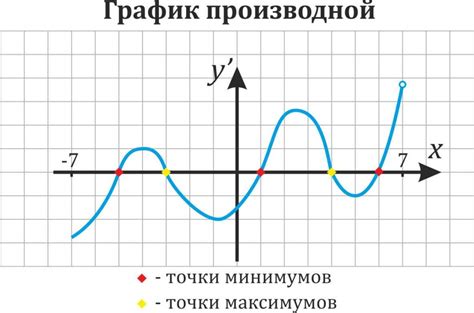
Для нахождения первообразной функции через точку М на графике необходимо определить координаты этой точки. Координаты точки М представляют собой значения аргумента функции и соответствующее значение функции в этом точке.
Если заданы координаты точки М(x0, y0), то первообразная функции f(x) через эту точку может быть найдена следующим образом:
- Определить общую первообразную функции f(x) с помощью интегрирования функции по переменной x.
- Подставить значение x0 в первообразную функцию и приравнять полученное значение к y0.
- Из полученного уравнения определить константу интегрирования.
- Подставить найденную константу в общую первообразную функции и получить искомую первообразную функцию f(x).
Таким образом, зная координаты точки М и общую первообразную функции f(x), можно определить конкретную первообразную функцию через эту точку. Это позволяет находить аналитический вид функции в случае, когда заданы только значения функции в конкретных точках.
Понятие точки на графике функции
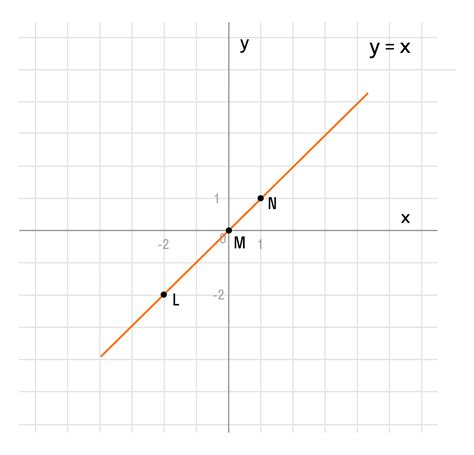
График функции представляет собой визуальное представление зависимости переменной величины от другой переменной. Он позволяет наглядно увидеть изменения значения функции при изменении аргумента.
Точка на графике функции представляет собой пару значений: значение аргумента и соответствующее ему значение функции. Таким образом, точка отображает конкретную точку на плоскости, которая является результатом подстановки значения аргумента в функцию.
Зная координаты точки на графике, можно определить, какие значения функции соответствуют данному аргументу. Также можно использовать точки на графике для нахождения первообразной функции через метод интерполирования, приближая формулу функции к заданной точке.
Проведя линию через несколько точек на графике, можно получить аппроксимацию функции и использовать ее для нахождения первообразной. Но необходимо помнить, что такой метод может давать лишь приближенные результаты, и точность будет зависеть от выбранного количества точек на графике и их расположения.
Точка на графике функции является одним из основных понятий, которые используются для анализа и работы с функциями. Она позволяет представить результаты функции в графическом виде и предоставляет интуитивное понимание контекста значения функции в определенной точке.
Задание точки М на графике
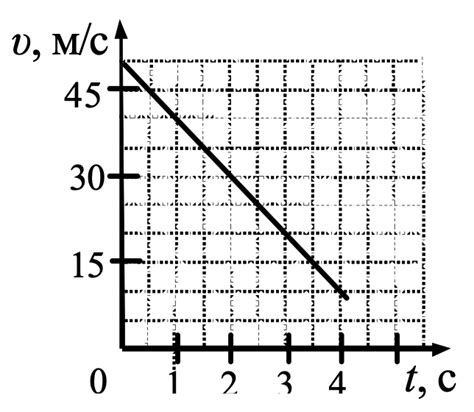
Для нахождения первообразной функции через точку М на графике необходимо определить координаты этой точки.
Обозначим заданную точку на графике как М(x0, y0), где x0 - абсцисса точки, а y0 - ордината точки.
Задание точки М на графике позволяет более точно определить искомую первообразную функцию. При нахождении первообразной функции через точку М, необходимо учитывать, что каждая точка на графике функции соответствует определенному значению функции в этой точке.
При решении задачи необходимо учесть основные принципы работы с графиками и нахождения первообразных функций. Разберитесь в основных понятиях и методах, связанных с нахождением первообразных функций через точку М на графике. Отметим, что решение такой задачи может потребовать применения различных методов, в зависимости от сложности исходной функции.
Задание точки М на графике обеспечивает более точное определение первообразной функции и позволяет решить более сложные задачи, связанные с нахождением криволинейного интеграла и вычислением площади под графиком функции.
Нахождение первообразной функции через точку М
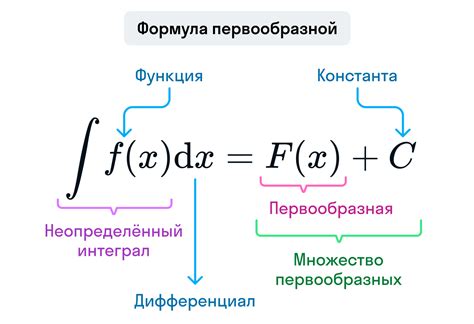
Процесс нахождения первообразной функции через точку М включает несколько шагов. Во-первых, необходимо выразить первообразную функцию через неизвестную константу. Затем мы можем использовать точку М, чтобы найти значение этой константы и получить окончательный вид первообразной функции.
Допустим, дана производная функции f'(x), и мы хотим найти первообразную функцию F(x). Если точка М на графике производной функции известна, то мы знаем, что производная функции в точке М равна значению F(x) в этой точке, то есть f'(M) = F(M).
Таким образом, мы можем записать уравнение f'(x) = F(x) + C, где С - неизвестная константа. Затем мы используем информацию о точке М, чтобы найти значение С. Например, если мы знаем, что F(M) = a, где a - известное число, мы можем найти С, подставив значения x = M и F(x) = a в уравнение.
После нахождения значения С, мы можем записать окончательный вид первообразной функции: F(x) = f(x) + C, где С - найденное значение.
Таким образом, нахождение первообразной функции через точку М на графике производной функции позволяет нам использовать информацию о ее значениях и поведении в определенной точке для определения значения неизвестной константы и получения окончательного вида функции. Этот метод особенно полезен, когда точка М на графике производной функции легко определяется и у нас есть дополнительная информация о ее значении.
Основные шаги при нахождении первообразной функции

Когда нам необходимо найти первообразную функцию для заданной функции, то мы должны выполнить несколько основных шагов. Эти шаги помогут нам найти функцию, производная которой равна исходной функции.
Шаг 1: Исследование функции.
Сначала мы должны внимательно изучить заданную функцию. Определить область ее определения и возможные точки разрыва. Понять, является ли функция непрерывной или имеет особые точки.
Шаг 2: Поиск правила дифференцирования.
Для нахождения первообразной функции полезно знать правила дифференцирования. Исследование исходной функции может помочь нам найти эти правила. Возможно, заданная функция является результатом применения одного из этих правил.
Шаг 3: Нахождение первообразной функции.
Используя правила дифференцирования и знания о функции, мы можем осуществить поиск первообразной функции. В процессе этого шага мы могли бы остановиться исходя из наших предположений и наличия данных. Но если у нас есть точка М на графике функции, то этот шаг становится намного проще.
Шаг 4: Использование точки на графике.
Если у нас есть точка М на графике функции, то мы можем использовать эту точку для нахождения константы интегрирования. Подставив координаты точки М в уравнение первообразной функции, мы сможем найти константу. Это поможет нам получить конкретное решение задачи.
Шаг 5: Проверка результата.
После того, как мы нашли первообразную функцию, необходимо проверить ее. Сделайте обратное дифференцирование для нашей найденной функции и убедитесь, что оно приводит к исходной функции. Если исходная функция и производная нашей найденной функции совпадают в области определения, то наше решение верно.
Теперь, зная основные шаги при нахождении первообразной функции через точку М на графике, мы сможем справиться с этой задачей. Важно помнить, что все шаги требуют внимательности и точности, чтобы получить правильное решение.