Правильная четырехугольная призма, также известная как квадратная призма, является одним из наиболее интересных геометрических тел. Это трехмерная фигура, состоящая из двух квадратных оснований и четырех прямоугольных боковых граней. Если вас интересует нахождение площади боковой поверхности правильной четырехугольной призмы, то вы попали по адресу!
Для того чтобы найти площадь боковой поверхности призмы, вам необходимо учесть несколько моментов. Во-первых, нужно знать длину стороны основания призмы и высоту призмы. Во-вторых, необходимо понимать, что площадь боковой поверхности вычисляется путем сложения площадей всех боковых граней призмы.
Для начала, найдите площадь одной боковой грани. Это прямоугольник со сторонами, равными длине стороны основания призмы и высоте призмы. Умножьте эти два значения, чтобы получить площадь одной боковой грани. Затем, умножьте площадь одной боковой грани на количество боковых граней призмы (в данном случае - 4), чтобы найти площадь боковой поверхности правильной четырехугольной призмы. Поздравляю, вы нашли ответ!
Что такое правильная четырехугольная призма
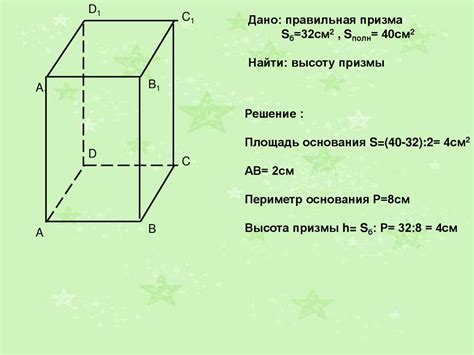
Основанием призмы служит четырехугольник, который называется базой и обладает свойством равномерности - все его стороны и углы равны. Угол между плоскостью базы и боковой гранью также является прямым, то есть равен 90 градусам.
Боковые стороны призмы являются прямоугольниками и в связи с равномерностью основания также имеют равные стороны и углы.
Правильная четырехугольная призма является одним из простейших типов призм и обладает рядом интересных свойств. Изучение ее характеристик и особенностей позволяет проводить различные геометрические вычисления, например нахождение площади боковой поверхности или объема.
Зачем нужно знать площадь боковой поверхности призмы
Понимание и вычисление площади боковой поверхности правильной четырехугольной призмы имеет практическую значимость в различных областях, особенно в строительстве и геометрии. Знание площади боковой поверхности призмы помогает определить необходимое количество материала для изготовления данной фигуры или для покраски ее стенок.
С учетом площади боковой поверхности призмы возможно точно определить, сколько краски или обоев понадобится для покрытия всех сторон этой геометрической фигуры. От знания площади боковой поверхности призмы зависит оптимальное расходование ресурсов и материалов.
Кроме того, знание площади боковой поверхности правильной четырехугольной призмы важно при проведении строительных работ и расчете стоимости проекта. Площадь боковой поверхности призмы позволяет оценить объем поверхности, который нужно обработать или защитить, что помогает определить стоимость выполнения работ.
Зная площадь боковой поверхности призмы, можно также проанализировать пропорции и форму фигуры, что может быть полезным при проектировании архитектурных объектов или элементов дизайна.
Таким образом, знание площади боковой поверхности призмы является важным аспектом в строительстве, геометрии и других областях, обеспечивая оптимальное использование ресурсов, рассчеты стоимости и достижение эстетически приятного дизайна.
Методы вычисления

Существует несколько методов вычисления площади боковой поверхности правильной четырехугольной призмы. Рассмотрим два наиболее популярных:
1. Метод разбиения на треугольники.
Для вычисления площади боковой поверхности призмы можно разбить ее на треугольники. Предположим, что у нас есть призма с основанием, представляющим правильный четырехугольник, а высота призмы известна. Если разбить боковую поверхность на треугольники, то площадь каждого треугольника можно вычислить по формуле S = (1/2) * a * h, где a - длина основания треугольника, h - высота треугольника. После этого необходимо сложить площади всех треугольников, чтобы получить площадь боковой поверхности призмы.
2. Метод использования площади основания.
Если мы знаем площадь основания призмы и ее высоту, то мы можем использовать формулу S = P * h, где P - периметр основания, h - высота призмы. Для правильного четырехугольника, периметр можно вычислить как P= 4 * a, где a - длина стороны основания. Подставляя известные значения, можно легко вычислить площадь боковой поверхности призмы.
Выбор метода вычисления площади боковой поверхности правильной четырехугольной призмы зависит от доступных данных и предпочтений человека, проводящего расчеты.
| Метод | Формула | Примечание |
|---|---|---|
| Разбиение на треугольники | S = (1/2) * a * h | a - длина основания треугольника, h - высота треугольника |
| Использование площади основания | S = P * h | P - периметр основания, h - высота призмы |
Метод через высоту и периметр
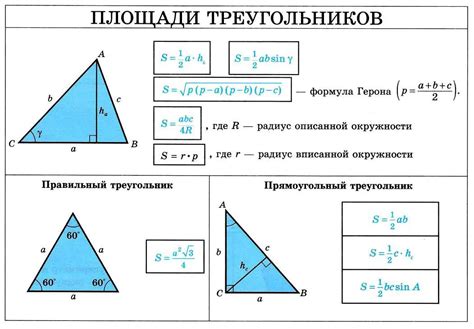
Для расчета площади боковой поверхности правильной четырехугольной призмы существует метод, основанный на высоте и периметре фигуры. Этот метод позволяет быстро и точно определить площадь.
Определение площади боковой поверхности происходит следующим образом:
- Найти высоту призмы. Высота четырехугольной призмы – это расстояние между двумя параллельными гранями фигуры.
- Найти периметр основания призмы. Периметр основания – это сумма длин всех сторон основания фигуры.
- Умножить высоту призмы на периметр основания. Это даст площадь одной боковой поверхности правильной четырехугольной призмы.
В итоге получим площадь боковой поверхности правильной четырехугольной призмы, выраженную в квадратных единицах. Этот метод можно применять для любой правильной четырехугольной призмы без искажений и несимметричных сторон.
Метод через длины сторон
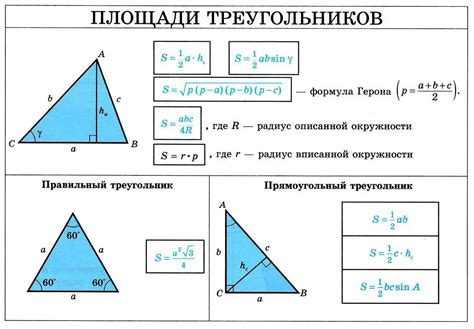
Если известны длины сторон четырехугольной призмы, можно легко найти площадь ее боковой поверхности. Чтобы это сделать, нужно знать, что боковая поверхность правильной четырехугольной призмы состоит из четырех равных прямоугольников.
Для нахождения площади каждого прямоугольника, нужно умножить длину одной из его сторон на длину призмы. Затем нужно сложить результаты всех четырех прямоугольников, чтобы получить общую площадь боковой поверхности призмы.
Пример формулы для нахождения площади боковой поверхности призмы:
- Найдите длину одной из сторон призмы - a.
- Найдите высоту призмы - h.
- Найдите площадь одного прямоугольника - S1 = a * h.
- Найдите общую площадь боковой поверхности призмы - S = 4 * S1 = 4 * a * h.
Используя этот метод, легко определить площадь боковой поверхности правильной четырехугольной призмы и использовать ее при решении различных задач и заданий.
Как применить формулы
Для расчета площади боковой поверхности правильной четырехугольной призмы необходимо применить следующую формулу:
S = p * h
Где:
- S - площадь боковой поверхности призмы;
- p - периметр основания призмы;
- h - высота призмы.
Перед применением формулы необходимо определить значения периметра основания и высоты призмы.
Сначала нужно найти периметр основания, который равен сумме длин всех сторон четырехугольника, образующего основание призмы.
Затем следует определить высоту призмы, которая является расстоянием между двумя параллельными сторонами основания.
После значений периметра основания и высоты призмы получены, их можно использовать в формуле для расчета площади боковой поверхности призмы.
Таким образом, следуя указанным шагам и применяя формулу, вы сможете легко найти площадь боковой поверхности правильной четырехугольной призмы.
Обратите внимание, что данная формула работает только для правильных четырехугольных призм с параллельными сторонами основания.
Пример вычисления площади боковой поверхности

Для того чтобы вычислить площадь боковой поверхности правильной четырехугольной призмы, нам необходимо знать длину одной из сторон основания и высоту призмы.
Пусть длина одной из сторон основания призмы равна a, а высота призмы равна h.
Площадь боковой поверхности призмы вычисляется по формуле:
| S = a * h |
Например, если длина одной из сторон основания призмы равна 5 см, а высота призмы равна 10 см, то площадь боковой поверхности вычисляется следующим образом:
| S = 5 см * 10 см | = 50 см² |
Таким образом, площадь боковой поверхности данной призмы равна 50 см².