Площадь круга является одним из основных параметров, определяющих геометрические свойства этой фигуры. Для расчета площади круга с помощью его диаметра существует простая формула, которую можно легко применить в любой ситуации.
Диаметром называется отрезок, соединяющий любые две точки на окружности круга и проходящий через его центр. Чтобы найти площадь круга по его диаметру, необходимо узнать значение этого параметра.
Формула для расчета площади круга по диаметру проста и понятна даже для начинающих:
Площадь круга = π * (диаметр / 2)2,
где π ("пи") - математическая константа, приближенное значение которой равно 3.14. Данный коэффициент обусловлен соотношением длины окружности к ее диаметру.
Теперь рассмотрим пример расчета площади круга по его диаметру. Пусть диаметр круга равен 10 см. Тогда, подставляя данные в формулу, получим:
Площадь круга = 3.14 * (10 / 2)2 = 3.14 * 25 = 78.5 см2.
Таким образом, площадь круга с диаметром 10 см составляет 78.5 см2.
Что такое площадь круга и как ее найти
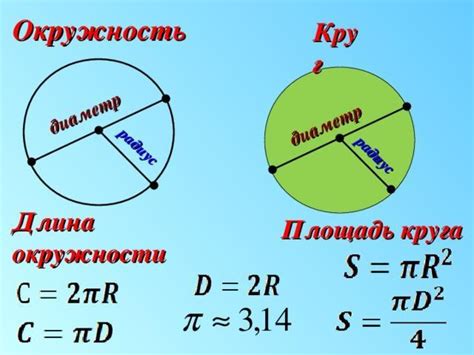
Для нахождения площади круга используется специальная формула. Если известен радиус R круга, то площадь S можно найти по формуле:
S = π * R^2
Где π (пи) - математическая константа, численно приближенно равная 3,14159.
Для удобства расчетов можно использовать значение π, приблизительно равное 3,14.
Пример расчета площади круга:
- Допустим, у нас есть круг с радиусом R = 5 см.
- Подставляем значение радиуса в формулу:
- S = 3,14 * 5^2
- S = 3,14 * 25
- S ≈ 78,5
Таким образом, площадь круга с радиусом 5 см составляет примерно 78,5 квадратных сантиметра.
Зная формулу и имея значение радиуса или диаметра круга, можно легко найти его площадь. Расчет площади круга полезен в различных областях, таких как геометрия, физика, инженерия и архитектура.
Строение площади круга
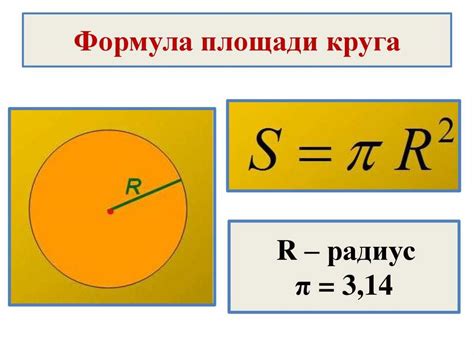
Радиус круга - это расстояние от центра круга до любой его точки. Он является половиной диаметра. Обозначается с помощью символа r.
Диаметр круга - это отрезок, соединяющий две точки на его границе и проходящий через его центр. Обозначается с помощью символа d.
Формула для расчета площади круга выглядит следующим образом:
S = πr2,
где S - площадь круга, π - математическая константа, примерное значение которой равно 3.14159, и r - радиус круга.
Для получения площади круга необходимо возвести радиус в квадрат и умножить на число π. Результат представляет собой площадь круга в квадратных единицах.
Например, если у нас есть круг с радиусом 5 см, то его площадь можно посчитать следующим образом:
S = π * 52 = 3.14159 * 25 = 78.53975,
что означает, что площадь круга составляет примерно 78.54 квадратных сантиметра.
Формула для расчета площади круга
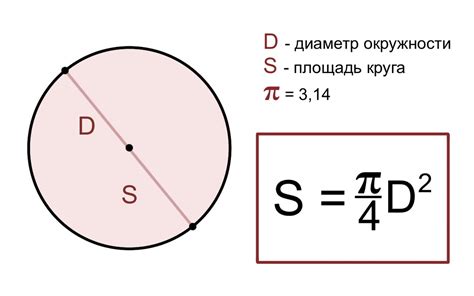
Для расчета площади круга необходимо знать его диаметр. Площадь круга вычисляется с помощью следующей формулы:
S = (π * d2) / 4
Где:
- S - площадь круга
- π (пи) - математическая константа, примерное значение равно 3,14159
- d - диаметр круга
Определив значение диаметра, можно легко вычислить площадь круга по данной формуле.
Например, для круга с диаметром 8 см:
- Вычисляем квадрат диаметра: d2 = (8 см) 2 = 64 см2
- Делим полученное значение на 4: (π * d2) / 4 = (π * 64 см2) / 4
- Умножаем полученное значение на значение пи: π ≈ 3,14159
- Получаем окончательный результат: S ≈ (3,14159 * 64 см2) / 4 ≈ 50,27 см2
Таким образом, площадь круга с диаметром 8 см составляет приблизительно 50,27 см2.
Примеры расчета площади круга
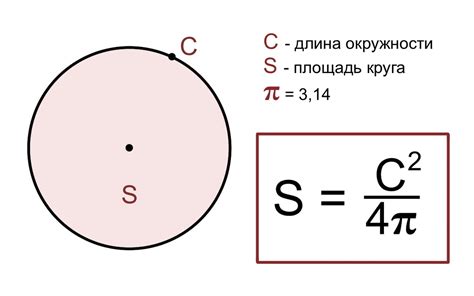
Для расчета площади круга необходимо знать его диаметр, который представляет собой расстояние между двумя точками на обратных сторонах круга, проходящими через его центр. Определим площадь круга с помощью формулы:
Площадь круга = π * (диаметр/2)^2
Где π (пи) - это математическая константа, приближенное значение которой равно 3,14159.
Давайте рассмотрим несколько примеров расчета площади круга:
Пример 1:
Допустим, у нас есть круг с диаметром 10 см. Чтобы найти площадь этого круга, применим формулу:
Площадь = 3,14159 * (10/2)^2
Площадь = 3,14159 * (5)^2
Площадь = 3,14159 * 25
Площадь ≈ 78,53975 см2
Таким образом, площадь круга с диаметром 10 см равна примерно 78,53975 квадратных сантиметров.
Пример 2:
Предположим, у нас есть круг с диаметром 6 метров. Применим формулу:
Площадь = 3,14159 * (6/2)^2
Площадь = 3,14159 * (3)^2
Площадь = 3,14159 * 9
Площадь ≈ 28,27431 м2
Таким образом, площадь круга с диаметром 6 метров составляет примерно 28,27431 квадратных метров.
Используя эту формулу, вы можете легко рассчитать площадь круга, зная его диаметр. Это полезное математическое понятие может быть применено в различных областях, таких как инженерия, строительство и геометрия.
Площадь круга и его диаметр

Формула для вычисления площади круга по диаметру выглядит следующим образом:
S = π * (d/2)²
где S – площадь круга, π (пи) – математическая константа, приблизительно равная 3,14159, а d – диаметр круга.
Например, допустим, у нас есть круг с диаметром 10 см. Чтобы найти его площадь, мы можем воспользоваться формулой:
S = 3.14159 * (10/2)² = 3.14159 * 5² = 78.54 см²
Таким образом, площадь круга с диаметром 10 см составляет 78.54 квадратных сантиметра.
Практическое применение площади круга

В архитектуре и строительстве площадь круга часто используется для расчета площади фундамента или пола. Например, если необходимо выложить круглый пол в комнате, можно вычислить площадь круга по заданному диаметру и затем определить количество материала, необходимое для его укладки.
В механике и инженерии площадь круга применяется для расчета площади сечения валов, поршней, колес и других деталей механизмов. Расчет площади круга позволяет определить прочность и устойчивость деталей, а также применять их в соответствии с требованиями безопасности и надежности.
В медицине площадь круга может использоваться для определения площади поверхности ожога или раны. Это помогает врачам оценить степень повреждения кожи и определить необходимость медицинского вмешательства.
Астрономы также используют площадь круга при измерении площади звезд и планет. Определение площади позволяет оценить размеры космических объектов и исследовать их физические характеристики.
Таким образом, площадь круга имеет широкий спектр применения и является важным понятием в различных областях науки и техники. Понимание и умение вычислять площадь круга позволяют решать разнообразные задачи и применять знания геометрии на практике.
Особенности расчета площади круга
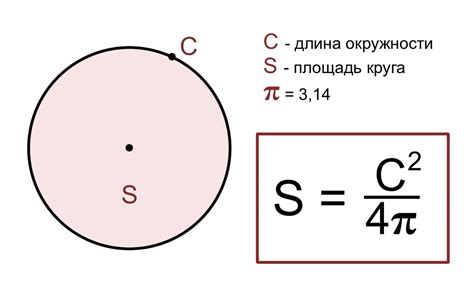
Расчет площади круга основывается на его радиусе или диаметре. Для расчета площади круга по диаметру используется формула:
S = π * (d/2)^2,
где S - площадь круга, d - диаметр круга, π (пи) - математическая константа, примерно равная 3.14159.
Для удобства расчета можно использовать следующую формулу:
S = π * r^2,
где S - площадь круга, r - радиус круга.
При использовании формулы, основанной на диаметре, необходимо учитывать, что диаметр в два раза больше радиуса. Поэтому, прежде чем использовать формулу S = π * (d/2)^2, необходимо разделить диаметр на 2.
Особенности расчета площади круга по диаметру позволяют быстро и точно определить эту характеристику фигуры, что широко применяется в геометрических расчетах и при решении различных задач.
Объем и площадь круга

Для нахождения площади круга по его диаметру существует простая формула:
S = π * (d/2)^2
где S – площадь круга, d – диаметр круга, а π – математическая константа, которую обычно принимают равной 3.14159 или просто 3.14.
Для примера, рассмотрим круг с диаметром 10 см. С помощью формулы, мы найдем:
| Параметр | Значение |
|---|---|
| Диаметр (d) | 10 см |
| Радиус (r) | 5 см |
| Площадь (S) | 78.54 см2 |
Таким образом, площадь круга с диаметром 10 см равна 78.54 см2.
Теперь рассмотрим вопрос о вычислении объема круга. Необходимо уточнить, что объем – это параметр, который относится к трехмерным фигурам, то есть круг в данном случае – это окружность, а не объемная фигура. Поэтому понятие объема обычно не применяется к кругу.