Круговой сектор – это часть плоскости, ограниченная двумя радиусами и дугой окружности между ними. Площадь кругового сектора – это важная характеристика, используемая в геометрии и различных научных и технических расчетах. Если известна длина дуги и радиус кругового сектора, можно легко найти его площадь.
Для вычисления площади кругового сектора по длине дуги существует специальная формула. Она основана на связи между углом сектора (измеряется в радианах), радиусом и длиной дуги. Формула выглядит следующим образом:
Площадь = (длина дуги * радиус) / 2
Эта формула является производной от формулы для вычисления площади круга. В круговом секторе длина дуги представляет долю от полной окружности, и соответственно площадь сектора является долей от площади круга.
Используя эту простую формулу, можно легко вычислить площадь кругового сектора по известной длине дуги и радиусу. Учитывайте, что значения длины дуги и радиуса должны быть выражены в одной и той же единице измерения.
Круговой сектор и его площадь: как рассчитать площадь по длине дуги
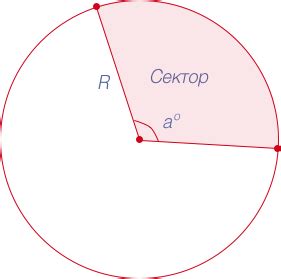
Расчет площади кругового сектора может быть полезным в различных областях, таких как геометрия, физика, инженерия и архитектура.
Формула для расчета площади кругового сектора в зависимости от длины дуги и радиуса дана следующим образом:
S = (π * r * L) / 360
где:
- S - площадь кругового сектора
- π - число пи, приближенно равное 3.14159
- r - радиус круга
- L - длина дуги круга
Для расчета площади кругового сектора необходимо знать радиус круга и длину дуги. Радиус можно измерить с помощью штангенциркуля или линейки, а длину дуги можно измерить с помощью ленты меры или метра. Затем просто подставьте значения в формулу и произведите вычисления.
Теперь вы знаете, как рассчитать площадь кругового сектора по длине дуги. Используйте эту информацию в своей практике, чтобы решать задачи и находить площади круговых секторов.
Понятие кругового сектора и его особенности
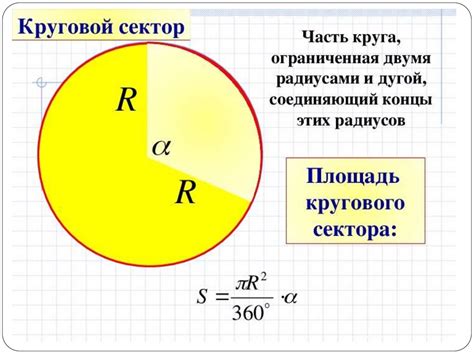
Круговой сектор обладает несколькими особенностями. Во-первых, он является фигурой с закругленными краями, которая имеет форму сектора. Во-вторых, его площадь зависит от длины дуги и радиуса. Чем больше длина дуги и радиус, тем больше площадь кругового сектора.
Круговой сектор широко используется в геометрии для решения различных задач. Он позволяет вычислять площадь сектора, а также находить угол, по которому повернут сектор относительно центра окружности. Формула для расчета площади кругового сектора выглядит следующим образом:
S = (π * r2 * α) / 360,
где S - площадь сектора, r - радиус окружности, α - центральный угол, определяющий длину дуги.
Длина дуги кругового сектора и ее измерение

Для измерения длины дуги кругового сектора используется радианная мера угла. Радиан - это единица измерения угла, которая соответствует центральному углу, заключающему между радиусами длиной, равной длине дуги круга.
Формула для расчета длины дуги кругового сектора:
L = r * θ
- L - длина дуги кругового сектора
- r - радиус окружности
- θ - центральный угол (в радианах)
Для измерения угла в радианах, используется следующая формула:
θ (в радианах) = θ (в градусах) * (π / 180)
где π является математической константой, приближенно равной 3.14159.
Измерение длины дуги кругового сектора может быть полезным при построении графиков функций, вычислении площади и объема тел, а также в других приложениях, где требуется точное значение длины участка окружности.
Формула расчета площади кругового сектора по длине дуги

Формула для расчета площади кругового сектора по длине дуги:
S = (l * r) / 2
где:
- S - площадь кругового сектора
- l - длина дуги
- r - радиус круга
Применение этой формулы позволяет быстро и точно вычислить площадь кругового сектора по заданным значениям длины дуги и радиуса круга. Используйте эту формулу в своих расчетах для нахождения площадей круговых секторов различных размеров и форм.
Примеры расчета площади кругового сектора

Для расчета площади кругового сектора необходимо знать длину дуги и радиус круга. Воспользуемся формулой:
S = (L * R) / 2
где S - площадь кругового сектора, L - длина дуги, R - радиус круга.
| Пример | Длина дуги (L) | Радиус круга (R) | Площадь кругового сектора (S) |
|---|---|---|---|
| Пример 1 | 10 | 5 | (10 * 5) / 2 = 25 |
| Пример 2 | 20 | 8 | (20 * 8) / 2 = 80 |
| Пример 3 | 15 | 3 | (15 * 3) / 2 = 22.5 |
Таким образом, площадь кругового сектора в первом примере равна 25, во втором примере - 80, а в третьем примере - 22.5.
Используя данную формулу, вы сможете быстро и легко рассчитывать площадь кругового сектора по известной длине дуги и радиусу круга.
Упражнения для практики расчета площади кругового сектора

Вот несколько упражнений, которые могут помочь вам улучшить навыки в расчете площади кругового сектора:
- Найдите площадь кругового сектора, если радиус круга равен 5 см, а длина дуги составляет 3 см.
- Определите площадь кругового сектора, если известно, что радиус круга равен 8 м, а длина дуги равна 10 м.
- Рассчитайте площадь кругового сектора, если радиус круга равен 6 дм, а длина дуги составляет 12 дм.
- Найдите площадь кругового сектора, если радиус круга равен 4 км, а длина дуги составляет 5 км.
- Определите площадь кругового сектора, если известно, что радиус круга равен 10 см, а длина дуги равна 15 см.
Выполнение этих упражнений поможет вам лучше понять формулу расчета площади кругового сектора и научиться применять ее в практических задачах. Помните, что формула для расчета площади кругового сектора выглядит следующим образом:
S = (r * l) / 2
Где S - площадь кругового сектора, r - радиус круга, l - длина дуги.
Продолжайте практиковаться в расчете площади кругового сектора, чтобы улучшить свои навыки и быть готовыми к решению сложных задач в будущем.
Применение площади кругового сектора в реальной жизни

Понимание и применение площади кругового сектора имеет практическое значение во многих областях нашей жизни. Вот несколько примеров:
- Геодезия и картография: При создании карт и планов, геодезисты и картографы используют площади круговых секторов для определения площадей участков земли или других территорий.
- Архитектура и строительство: Площадь кругового сектора может быть использована для расчета площади крыши или фундамента, который имеет форму сектора круга. Это помогает строителям правильно оценить количество материалов, необходимых для проекта.
- Дизайн и графика: В дизайне и графике площади круговых секторов могут использоваться для создания пропорциональных диаграмм, статистических графиков или показателей широты использования различных элементов в дизайне.
- Физика и инженерия: Площадь кругового сектора может быть применена для расчета площади сектора проволоки или материала, который используется в проводных цепях или электрических устройствах.
- Медицина: В некоторых случаях площадь кругового сектора может быть использована для расчета площади поверхности кожи, например, для определения площади ожогов.
Это лишь несколько примеров того, как площадь кругового сектора может быть применена в реальной жизни. Знание этой формулы позволяет нам более точно и эффективно решать реальные задачи и проблемы в различных областях.