Куб – это геометрическая фигура, все грани которой являются квадратами. Для нахождения площади куба мы должны знать только длину одной его грани, так как все грани куба одинаковы по размеру. Вычисление площади куба основывается на формуле, которая учитывает количество граней и их размер.
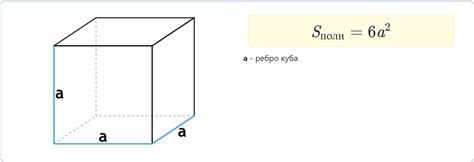
Формула нахождения площади куба: S = 6 * a^2, где S – площадь куба, а – длина одной грани. Иными словами, площадь куба равна шести площадям его одинаковых граней, каждая из которых равна kv^2, где k – коэффициент, равный 6, а v – длина одной грани.
Чтобы применить эту формулу, измерьте длину одной грани куба. Затем возведите это значение в квадрат и умножьте на 6. Полученный результат будет площадью куба.
Наконец, важно отметить, что площадь куба измеряется в квадратных единицах, таких как квадратные метры или квадратные сантиметры. Расчет площади куба может быть полезен при проектировании боксов или контейнеров, а также при решении задач в физике или геометрии.
Что такое площадь куба и как ее найти?
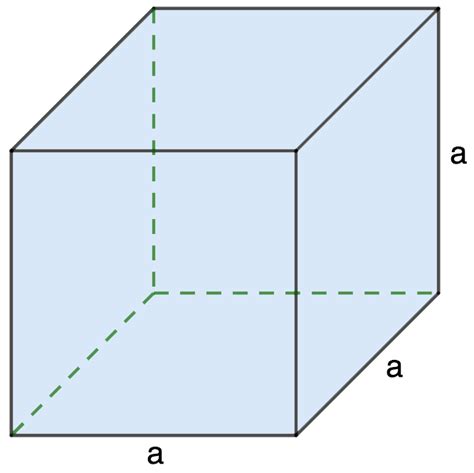
Для того чтобы найти площадь куба, нужно найти площадь одной его грани и затем умножить ее на 6, так как куб имеет 6 граней. Формула для нахождения площади грани куба выглядит следующим образом:
- Измерьте длину одной стороны куба
- Возьмите результат и возвести его в квадрат
- Полученное значение умножьте на 6
Например, если длина одной стороны куба равна 4 см, то площадь грани будет 4 * 4 = 16 см². А общая площадь куба будет 16 * 6 = 96 см².
Нахождение площади куба имеет практическое применение в различных областях, таких как строительство, архитектура, геометрия и другие. Зная площадь куба, можно, например, рассчитать необходимое количество материала для его покрытия или оценить объем содержимого кубического контейнера.
Определение площади куба
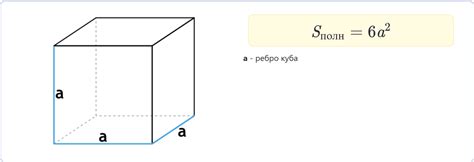
Для того чтобы найти площадь куба, достаточно знать площадь одной его грани. Формула площади куба выглядит следующим образом:
S = 6a²,
где S - площадь куба, a - длина стороны грани куба.
Таким образом, чтобы найти площадь куба, необходимо возвести длину стороны грани в квадрат и умножить полученное значение на 6.
Геометрическая формула для вычисления площади куба

Для вычисления площади куба нужно умножить площадь одной из его граней на 6, так как у куба 6 граней и все они равны по площади. Формула выглядит следующим образом:
| Площадь куба | = | 6 | × | площадь одной грани куба |
Площадь одной грани куба равна квадрату длины его ребра. Таким образом, формула площади куба может быть переписана:
| Площадь куба | = | 6 | × | (длина ребра куба) | ² |
Используя эту формулу, можно легко вычислить площадь куба, зная длину его ребра. Эта формула также подходит для нахождения площади прямоугольного параллелепипеда, если все его стороны равны.
Шаги для нахождения площади куба

Чтобы найти площадь куба, нужно выполнить несколько простых шагов:
1. Определите длину ребра куба. Представьте, что вам дана сторона куба и вам нужно найти его площадь.
2. Возьмите заданную сторону и умножьте ее саму на 6. Это связано с тем, что у куба 6 одинаковых граней, и для нахождения площади необходимо учесть все стороны.
3. Полученное значение будет площадью куба. Ответ представляет собой численное значение, которое описывает общую площадь поверхности куба.
Надеюсь, этот пошаговый алгоритм поможет вам понять, как найти площадь куба и измерить поверхность данной геометрической фигуры.
Пример вычисления площади куба
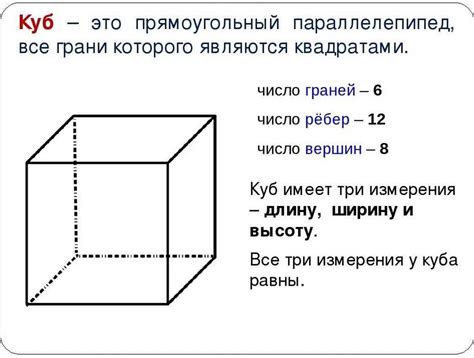
Чтобы найти площадь куба, необходимо знать длину одной из его сторон. Пусть длина стороны куба равна a.
Площадь грани куба равна произведению длины стороны a на саму себя (Sгр = a * a).
Так как куб имеет 6 граней, его общая площадь равна шести произведению площади грани на 1 (Sк = 6 * Sгр).
Таким образом, площадь куба может быть вычислена по формуле S = 6a2.
Интерпретация площади куба в реальном мире
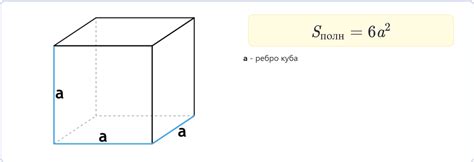
В архитектуре, площадь куба может быть использована для расчета жилой площади помещений. Площадь стен куба можно использовать для определения необходимого количества строительных материалов, таких как краска или обои. Кроме того, зная площадь куба, можно рассчитать объем помещения.
В мебельной индустрии, площадь куба шкафа или комода позволит определить его вместимость. Зная площадь каждой грани куба, производители мебели могут определить необходимый объем материала для изготовления задних стенок или полок шкафа.
В научных исследованиях, площадь поверхности куба играет роль в изучении явлений теплоотдачи или диффузии. Чем больше площадь контакта, тем эффективнее происходит передача тепла или вещества между частицами.
Кроме того, площадь куба может быть интерпретирована в контексте дизайна или графики. Грани куба можно использовать как поверхности для создания различных графических элементов или для реализации разнообразных идей.
Зачем нужно знать площадь куба?
Знание площади куба имеет несколько применений и может быть полезно в различных ситуациях. Вот несколько причин, почему важно знать площадь куба:
- Расчет объема: зная площадь одной из сторон куба, можно вычислить его объем. Объем куба является основной характеристикой, которая позволяет определить, насколько вместительным является данный объект. Например, зная площадь бассейна, можно оценить, сколько воды нужно для его заполнения.
- Расчет поверхности: зная площадь одной стороны куба, можно вычислить его полную поверхность. Зная полную поверхность куба, можно определить, сколько материала понадобится для его облицовки или покраски.
- Проектирование и строительство: зная площадь куба, архитекторы, инженеры и строители могут определить необходимые материалы и ресурсы для постройки объекта, а также спланировать его внутреннее пространство и функциональность.
- Учет и хранение: зная площадь куба, можно эффективно использовать пространство для размещения предметов, например, в грузовом контейнере или на складе. Также, зная площадь кубического объекта, можно определить его объем и, таким образом, учесть его при подсчете объема или веса.
- Расчет поверхностей и покрытий: зная площадь куба, можно расчитать необходимое количество краски, обоев или плитки для его покрытия. Это поможет сократить расход материалов и избежать дополнительных расходов.
Итак, знание площади куба является важным инструментом, который помогает в решении разнообразных задач и упрощает процессы проектирования, строительства, хранения и повседневного использования кубических объектов.
Полезные советы при вычислении площади куба
Вычисление площади куба может быть простым и интересным процессом, если вы знаете некоторые полезные советы. Вот несколько рекомендаций, которые помогут вам в этом:
- Запомните формулу: площадь боковой поверхности куба равна удвоенному произведению длины ребра на высоту куба. Формула выглядит следующим образом: S = 4 * a * a, где S - площадь боковой поверхности куба, a - длина ребра куба.
- Используйте правильные единицы измерения: при вычислении площади куба, убедитесь, что ваша длина ребра и высота измерены в одной и той же единице. Если вы используете метры для измерения ребра, используйте также метры для измерения высоты.
- Учтите все грани куба: площадь куба включает в себя площади всех его граней. Помимо боковой поверхности, учтите верхнюю и нижнюю грани куба. Чтобы получить общую площадь, сложите площади всех граней.
- Не забудьте удвоить результат: помните, что площадь боковой поверхности куба необходимо удвоить. После вычисления площади боковой поверхности, умножьте полученное значение на 2, чтобы получить общую площадь куба.
- Проверьте свои вычисления: всегда хорошо проверить свои результаты, особенно при работе с формулами. Проверьте свои вычисления, используя разные методы, чтобы убедиться в правильности результата.
Следуя этим полезным советам, вы сможете легко вычислить площадь куба и успешно решать задачи, связанные с этой темой.
Мы вывели формулу для вычисления площади одной грани куба: S = a * a, где a - длина стороны куба.
Далее, мы выяснили, что у куба 6 граней, поэтому площадь всего куба можно найти, умножив площадь одной грани на 6: S_куба = 6 * S_грани.
Используя эти формулы, можно легко вычислить площадь любого куба, зная длину его стороны.
Теперь вы знаете, как найти площадь куба и можете применить полученные знания в решении задач из различных областей математики и физики.