Квадрат - одна из самых простых и популярных геометрических фигур. Он имеет четыре стороны, причем все они равны и образуют прямые углы. Площадь квадрата - это показатель, который характеризует его площадь, то есть особенность его геометрического строения. Знание формулы для расчета площади квадрата - это основа для решения различных задач в геометрии и не только.
Формула нахождения площади квадрата:
S = a^2
где S - площадь квадрата, а a - длина стороны.
Таким образом, чтобы найти площадь квадрата, необходимо возвести длину его стороны в квадрат. Это правило справедливо всегда, вне зависимости от значения a. Например, если длина стороны квадрата равна 5 см, то его площадь будет равна 25 квадратным сантиметрам.
Что такое площадь квадрата?

Площадью квадрата называется величина, которая определяет площадь плоской фигуры, образованной квадратом. Площадь квадрата можно найти, зная длину его стороны и применяя простую математическую формулу.
Формула для нахождения площади квадрата выглядит следующим образом:
| Площадь квадрата (S) | = | Длина стороны (a) | × | Длина стороны (a) | = | a² |
Таким образом, площадь квадрата равна квадрату длины его стороны.
Например, если сторона квадрата равна 5 сантиметров, то его площадь будет:
| Площадь квадрата (S) | = | 5 см | × | 5 см | = | 25 см² |
Таким образом, площадь квадрата со стороной 5 сантиметров равна 25 квадратным сантиметрам.
Знание площади квадрата может быть полезным при решении задач, связанных с геометрией и измерением площадей. Оно также является основой для понимания других геометрических понятий, таких как периметр, объем и т.д.
Определение площади квадрата
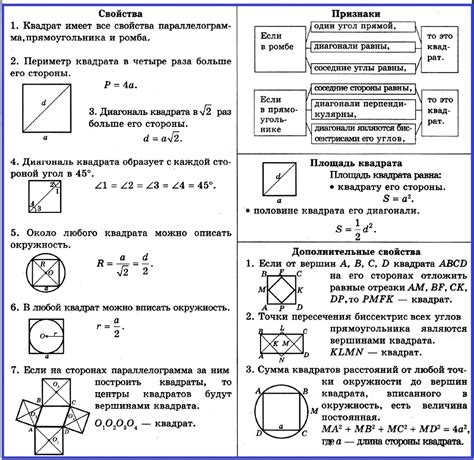
Для определения площади квадрата используется формула:
- Умножьте длину одной стороны квадрата на саму себя (a * a).
Таким образом, площадь квадрата равна квадрату длины его стороны.
Например, если сторона квадрата равна 5 см, то площадь будет:
- 5 см * 5 см = 25 см2
Таким образом, площадь квадрата со стороной 5 см составляет 25 квадратных сантиметров.
Зная формулу и длину стороны квадрата, вы можете легко определить его площадь.
Формула для вычисления площади квадрата

Математически это можно записать следующим образом:
Площадь = a2
Где "a" - это длина стороны квадрата.
Например, если длина стороны квадрата равна 4 единицам, то формула будет выглядеть следующим образом:
Площадь = 42 = 16
Таким образом, площадь квадрата со стороной длиной 4 единицы будет равна 16 квадратным единицам.
Примеры вычисления площади квадрата
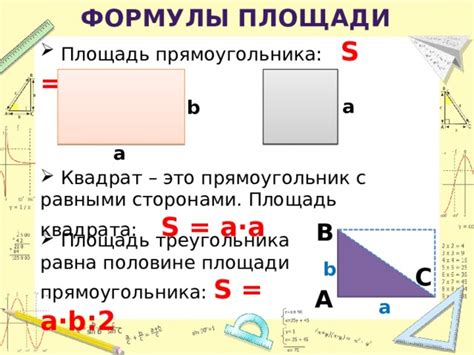
Рассмотрим несколько примеров, чтобы наглядно представить, как вычислить площадь квадрата.
Пример 1:
Пусть дан квадрат со стороной длиной 5 см. Чтобы найти его площадь, нужно возвести эту сторону в квадрат:
Площадь квадрата = длина стороны × длина стороны = 5 см × 5 см = 25 см².
Пример 2:
Если известна площадь квадрата и нужно найти длину его стороны, то применяем обратную операцию - извлечение квадратного корня. Например, площадь квадрата равна 36 см². Тогда:
Длина стороны = √(площадь квадрата) = √36 см² = 6 см.
Пример 3:
Иногда длина стороны квадрата задана в других единицах измерения, например, в метрах. Допустим, сторона равна 2 м. Чтобы найти площадь, нужно преобразовать длину стороны в квадратную единицу:
Площадь квадрата = длина стороны × длина стороны = 2 м × 2 м = 4 м².
| Сторона квадрата (см) | Площадь квадрата (см²) |
|---|---|
| 2 | 4 |
| 4 | 16 |
| 6 | 36 |
| 8 | 64 |
Надеюсь, примеры помогут вам лучше понять, как вычислить площадь квадрата и применить это знание на практике!