Площадь квадрата с известной диагональю может быть получена при помощи специальной формулы, которая позволяет расчитать площадь фигуры только на основе ее диагонали. Этот метод является удобным и простым способом нахождения площади квадрата, особенно когда известна только длина его диагонали.
Формула для нахождения площади квадрата с заданной диагональю основана на связи между диагональю и стороной квадрата. Важно отметить, что квадрат имеет все стороны равными между собой, а диагональ делит его на два равных прямоугольных треугольника.
Чтобы найти площадь квадрата, необходимо сначала найти длину его стороны по формуле, затем возвести эту длину в квадрат. Итак, если известна длина диагонали квадрата, можно использовать следующую формулу: сторона = диагональ / √2. Затем, для того чтобы получить площадь квадрата, необходимо возвести сторону в квадрат по формуле: площадь = сторона².
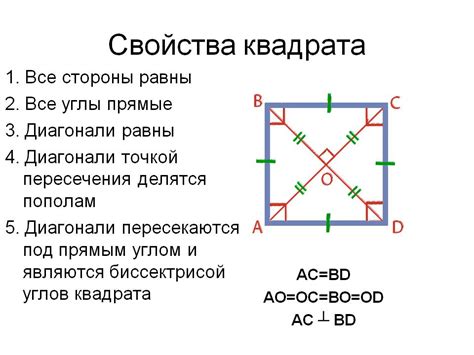
Квадрат: определение и основные характеристики
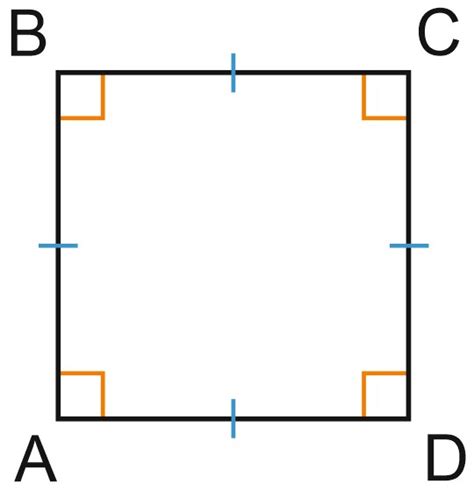
Основные характеристики квадрата:
- Сторона - каждая из четырех одинаковых и параллельных отрезков, соединяющих вершины квадрата.
- Диагональ - отрезок, соединяющий две противоположные вершины квадрата и проходящий через его центр. Длина диагонали можно найти по формуле: диагональ = сторона * √2.
- Углы - все углы квадрата равны 90 градусам.
- Периметр - сумма длин всех сторон квадрата. Периметр можно найти по формуле: периметр = 4 * сторона.
- Площадь - площадь квадрата можно найти по формуле: площадь = сторона * сторона.
Квадрат широко используется в геометрии и математике, а также является основой для конструирования других геометрических фигур и объектов. Понимание его определения и основных характеристик является важным для решения различных задач и вычислений.
Формула расчета длины стороны квадрата по диагонали
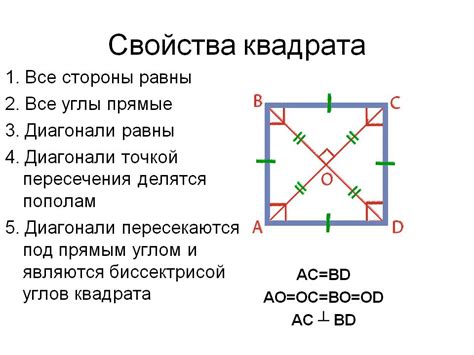
Для расчета длины стороны квадрата по известной диагонали можно использовать следующую формулу:
Сторона квадрата = Диагональ / (√2)
Где:
- Сторона квадрата - длина одной из сторон квадрата
- Диагональ - длина диагонали квадрата
- √2 - квадратный корень из числа 2, приближенное значение округляется до необходимой точности
Например, если известна длина диагонали квадрата, равная 10, то длина стороны будет равна 10 / (√2) ≈ 7.071.
Таким образом, используя данную формулу, можно легко и быстро расчитать длину стороны квадрата по известной диагонали.
Как найти площадь квадрата по диагонали
Для расчета площади квадрата с заданной диагональю необходимо знать формулу, которая связывает диагональ и сторону квадрата. Чтобы найти площадь квадрата по диагонали, следуйте следующим шагам:
- Найдите длину стороны квадрата. Для этого используйте теорему Пифагора: диагональ квадрата является гипотенузой прямоугольного треугольника, у которого стороны равны длине стороны квадрата. Используя формулу, найдите длину стороны квадрата, например, если диагональ равна d, то сторона квадрата равна d/√2.
- Возведите длину стороны квадрата в квадрат. Полученное значение будет площадью квадрата.
Например, если дана диагональ квадрата d = 10 см, то:
Длина стороны квадрата: 10 см / √2 ≈ 7.07 см
Площадь квадрата: (7.07 см)² ≈ 50 см²
Теперь вы знаете, как найти площадь квадрата, если известна его диагональ.
Что такое диагональ квадрата и как она связана с его стороной?
Связь между диагональю квадрата и его стороной можно выразить с помощью геометрических формул. Если известна длина диагонали квадрата, то можно найти длину его стороны. Для этого можно воспользоваться формулой:
сторона квадрата = диагональ / √2
Таким образом, зная длину диагонали, можно легко рассчитать сторону и площадь квадрата. Зная сторону, можно также найти диагональ с помощью обратной формулы:
диагональ квадрата = сторона * √2
Используя эти формулы, можно связать диагональ и сторону квадрата и легко рассчитать их значения.
Практический пример расчета площади квадрата по диагонали
Для этого мы можем воспользоваться формулой площади квадрата, которая состоит из двух шагов:
- Найдем сторону квадрата по формуле с = d / √2, где d - диагональ квадрата.
- Возведем полученную сторону в квадрат и получим площадь квадрата по формуле s = c², где c - сторона квадрата.
Применяя эти шаги к нашему примеру, получаем следующий результат:
| Шаг | Вычисление | Результат |
|---|---|---|
| 1 | c = 10 / √2 | c ≈ 10 / 1.414 |
| 2 | s = c² | s ≈ (10 / 1.414)² |
Итак, площадь квадрата с диагональю 10 сантиметров будет примерно равна 50 квадратным сантиметрам.
Зачем нужно знать формулу расчета площади квадрата по диагонали?

Знание формулы расчета площади квадрата по диагонали может быть полезным во многих ситуациях.
- Оценка площади квадратной поверхности. Зная диагональ квадрата, можно точно определить его площадь. Это может быть полезно при планировании использования пространства, например, при рассчете площади комнаты для меблировки или для расчета площади участка для строительства.
- Решение геометрических задач. Формула расчета площади квадрата по диагонали может быть полезна при решении различных геометрических задач, например, при нахождении площади трапеции, вписанной в квадрат, или при нахождении площади круглой поверхности, ограниченной квадратом.
- Учебные цели. Изучение формулы для расчета площади квадрата по диагонали помогает развить навыки работы с геометрическими фигурами и применение математических формул.
Знание формулы расчета площади квадрата по диагонали может быть полезным как в повседневной жизни, так и в академическом контексте, и помогает лучше понять и использовать геометрические принципы и концепции.
Как использовать формулу расчета площади квадрата по диагонали в повседневной жизни

Одна из практических областей, где можно применить формулу расчета площади квадрата по диагонали, - это строительство. Представим ситуацию, когда вам необходимо узнать площадь квадратного участка земли. Измеряя диагональ участка при помощи известного инструмента, вы можете легко рассчитать площадь квадрата, на котором расположен ваш участок. Это будет полезно для определения стоимости материалов, планирования ландшафта и других строительных операций.
Другой сферой, где формула может найти применение, является дизайн интерьера. Представьте, что вам необходимо купить квадратный ковер для комнаты. Зная диагональ комнаты, можно расчитать площадь необходимого ковра. Это поможет вам выбрать подходящий размер ковра и избежать покупки либо недостаточно большого, либо слишком большого ковра.
Также формула может быть полезна для архитекторов и дизайнеров, которые работают с квадратными пространствами. Площадь квадрата может быть использована для расчета объемов материалов, необходимых для отделки, оценки затрат на ремонт и т.д.