Умение вычислять площадь плоских геометрических фигур - это важный навык для любого, кто интересуется математикой или нуждается в решении практических задач.
Квадрат, треугольник и прямоугольник - это классические фигуры, для которых существуют простые и надежные формулы вычисления площади. Их можно использовать в самых разных ситуациях - от строительства забора до расчета количества квадратных метров обоев для комнаты.
Итак, расчет площади квадрата основан на знании длины его стороны. Формула для вычисления площади этой фигуры очень проста - нужно лишь умножить длину стороны на саму себя.
Площадь треугольника, в свою очередь, зависит от длины его основания и высоты. Формула для вычисления площади треугольника следующая: площадь равна половине произведения длины основания на соответствующую высоту.
Прямоугольник - это еще одна простая геометрическая фигура, для которой вычисление площади не вызовет затруднений. Формула для этой фигуры также проста - нужно лишь перемножить длину и ширину прямоугольника.
Используя эти простые формулы и знания математики, вы сможете быстро и точно вычислять площадь квадрата, треугольника и прямоугольника. А что самое главное, это знание будет полезным в самых разных ситуациях, помогая вам решать различные задачи и проблемы.
Формула для вычисления площади квадрата

Площадь квадрата можно вычислить, умножив длину одной его стороны на саму себя. Формула для вычисления площади квадрата имеет вид:
S = a2,
где S - площадь квадрата, а - длина стороны квадрата.
Например, если сторона квадрата равна 5 единицам, то площадь квадрата будет равна:
S = 52 = 25.
Таким образом, площадь квадрата со стороной равной 5 единицам будет равна 25 единицам квадратным.
Как найти площадь квадрата: формула и пример вычисления
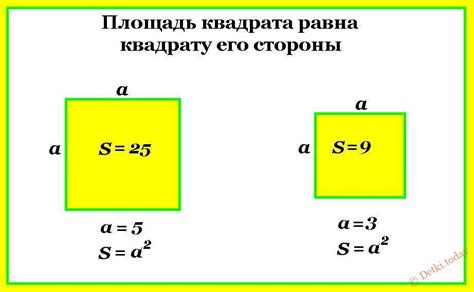
Площадь квадрата можно вычислить, зная длину его стороны. Формула для нахождения площади квадрата очень проста: нужно возвести длину стороны в квадрат.
Формула для нахождения площади квадрата:
| S = a², |
где S - площадь квадрата, a - длина стороны квадрата.
Рассмотрим пример вычисления площади квадрата:
Допустим, у нас есть квадрат со стороной длиной 5 см. Чтобы найти площадь данного квадрата, мы возводим длину стороны в квадрат:
| a = 5 см, |
| S = 5² = 25 см². |
Таким образом, площадь квадрата со стороной 5 см равна 25 квадратных сантиметров.
Формула для вычисления площади треугольника
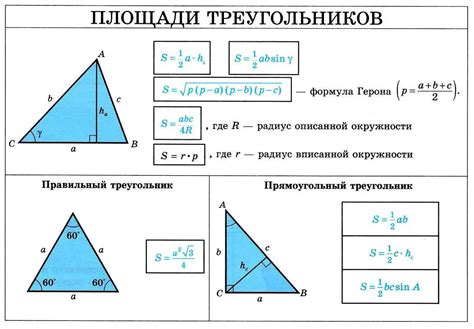
Формула для вычисления площади треугольника имеет вид:
S = (a * h) / 2
где:
S - площадь треугольника
a - длина основания треугольника
h - высота треугольника, проведенная к основанию
Чтобы вычислить площадь треугольника, нужно знать длину его основания и высоту. Основание - это любая сторона треугольника, а высота - перпендикуляр, опущенный из вершины треугольника на основание.
Пример расчета площади треугольника:
Пусть длина основания треугольника равна 8 см, а высота равна 6 см. Используя формулу для вычисления площади треугольника, получаем:
S = (8 * 6) / 2 = 24 см2
Таким образом, площадь треугольника равна 24 квадратным сантиметрам.
Формула для вычисления площади треугольника позволяет быстро и точно определить его площадь при заданных значениях основания и высоты. Зная эту формулу, вы сможете вычислять площадь треугольников в различных задачах геометрии и решать связанные с ними задачи.
Как найти площадь треугольника: формула и пример вычисления
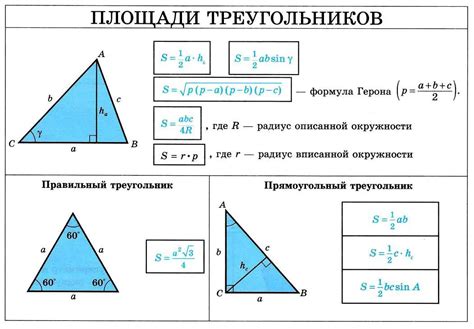
Формула Герона позволяет вычислить площадь треугольника по длинам его сторон. Для этого необходимо знать значения всех трех сторон треугольника.
Формула для расчета площади треугольника по формуле Герона:
S = √(p(p-a)(p-b)(p-c)),
где S - площадь треугольника;
a, b, c - длины сторон треугольника;
p - полупериметр треугольника, который вычисляется по формуле p = (a + b + c) / 2.
Ниже приведен пример вычисления площади треугольника с заданными сторонами:
- Допустим, у нас есть треугольник со сторонами a = 5, b = 7 и c = 8.
- Вычисляем полупериметр треугольника: p = (5 + 7 + 8) / 2 = 20 / 2 = 10.
- Подставляем значения в формулу для расчета площади: S = √(10(10-5)(10-7)(10-8)) = √(10 * 5 * 3 * 2) = √300 = 17,32 (округляем до двух знаков после запятой).
Таким образом, площадь треугольника с заданными сторонами равна 17,32 квадратных единиц.
Это был пример расчета площади треугольника по формуле Герона. Не забывайте, что существуют и другие способы вычисления площади треугольника в зависимости от известных данных, например, по формуле для прямоугольного треугольника или при известной высоте треугольника.
Формула для вычисления площади прямоугольника
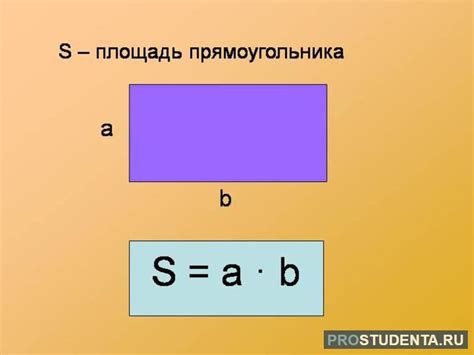
Площадь = длина × ширина
Для примера, представим прямоугольник, у которого длина равна 5 единицам, а ширина равна 3 единицам. Чтобы найти его площадь, нужно умножить длину на ширину:
- Площадь = 5 × 3
- Площадь = 15
Таким образом, площадь этого прямоугольника составляет 15 квадратных единиц.
Эта формула может быть использована для вычисления площади прямоугольников различных размеров. Просто запишите значения длины и ширины прямоугольника в формулу и выполните несложные вычисления, чтобы получить его площадь.