Прямой параллелепипед - это трехмерная геометрическая фигура, у которой все грани являются прямоугольниками. Правильно вычислить площадь его поверхности - очень важно, так как это позволяет нам определить, сколько материала нам потребуется для ее покрытия или для расчета необходимого объема контейнера.
Формула для вычисления площади поверхности прямого параллелепипеда зависит от его размеров. Площадь поверхности параллелепипеда вычисляется путем сложения площадей всех его граней. Представим, что у нас есть прямой параллелепипед со сторонами a, b и c.
Формула для вычисления площади поверхности параллелепипеда:
Площадь поверхности = 2ab + 2bc + 2ac
Например, допустим, у нас есть прямой параллелепипед со сторонами 2, 3 и 4. Чтобы найти площадь его поверхности, мы можем использовать формулу:
Площадь поверхности = 2 * 2 * 3 + 2 * 3 * 4 + 2 * 2 * 4 = 12 + 24 + 16 = 52
Таким образом, площадь поверхности прямого параллелепипеда со сторонами 2, 3 и 4 равна 52 квадратным единицам.
Определение прямого параллелепипеда и его поверхности
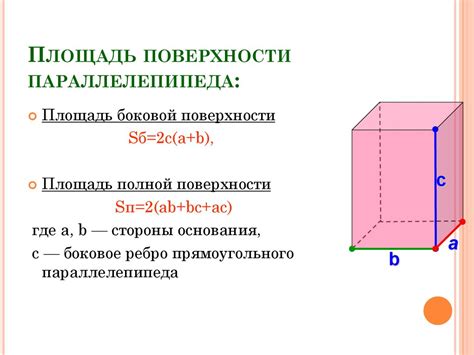
Поверхность прямого параллелепипеда состоит из шести прямоугольных граней. Чтобы вычислить площадь поверхности, нужно найти площади всех шести граней и сложить их вместе. Для этого можно использовать формулу:
Площадь поверхности = 2 * (длина * ширина + ширина * высота + длина * высота)
Например, предположим, что у нас есть прямой параллелепипед с длиной 4 см, шириной 3 см и высотой 2 см. Чтобы найти площадь его поверхности, воспользуемся формулой:
| Грань | Длина | Ширина | Площадь |
|---|---|---|---|
| Грань 1 | 4 см | 3 см | 12 кв. см |
| Грань 2 | 4 см | 2 см | 8 кв. см |
| Грань 3 | 3 см | 2 см | 6 кв. см |
| Грань 4 | 4 см | 3 см | 12 кв. см |
| Грань 5 | 3 см | 2 см | 6 кв. см |
| Грань 6 | 4 см | 2 см | 8 кв. см |
Теперь можем сложить площади всех шести граней:
Площадь поверхности = 12 кв. см + 8 кв. см + 6 кв. см + 12 кв. см + 6 кв. см + 8 кв. см = 52 кв. см
Таким образом, площадь поверхности прямого параллелепипеда со сторонами 4 см, 3 см и 2 см равна 52 квадратным сантиметрам.
Формула для вычисления площади поверхности
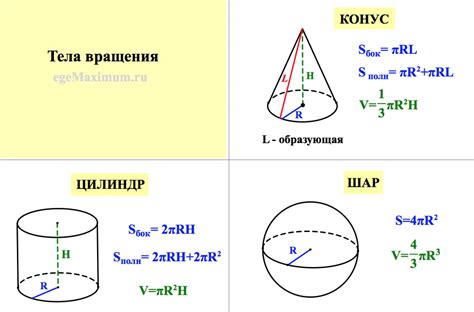
Площадь поверхности прямого параллелепипеда может быть вычислена с использованием формулы:
S = 2ab + 2bc + 2ac
где:
- S - площадь поверхности;
- a, b, c - длины ребер параллелепипеда.
Для вычисления площади поверхности прямого параллелепипеда необходимо умножить сумму попарных произведений длин ребер на 2 и сложить полученные значения.
Например, если длины ребер параллелепипеда равны 4, 5 и 6, то площадь поверхности будет:
- S = 2 * 4 * 5 + 2 * 5 * 6 + 2 * 4 * 6 = 40 + 60 + 48 = 148.
Таким образом, площадь поверхности прямого параллелепипеда с ребрами длиной 4, 5 и 6 равна 148 квадратных единиц.
Пример 1: Вычисление площади поверхности прямого параллелепипеда

Рассмотрим пример вычисления площади поверхности прямого параллелепипеда на практике. Предположим, что у нас есть прямоугольный параллелепипед со следующими размерами:
- Длина: 5 см
- Ширина: 4 см
- Высота: 3 см
Для начала, нам необходимо найти площадь каждой поверхности параллелепипеда отдельно.
Площадь поверхности площади прямоугольного параллелепипеда можно вычислить по формуле:
S = 2 * (длина * ширина + длина * высота + ширина * высота)
Подставим значения в формулу:
S = 2 * (5 * 4 + 5 * 3 + 4 * 3)
Выполняем вычисления:
S = 2 * (20 + 15 + 12) = 2 * 47 = 94
Итак, площадь поверхности этого прямого параллелепипеда составляет 94 квадратных сантиметра.
Пример 2: Расчет площади поверхности параллелепипеда с нестандартными размерами
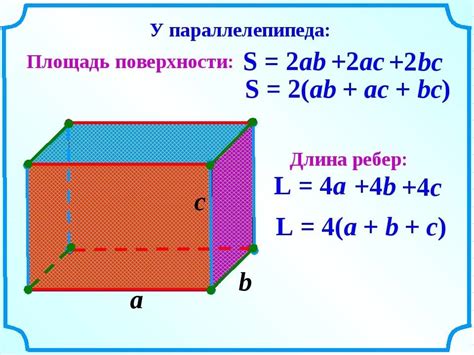
Для наглядности рассмотрим пример расчета площади поверхности параллелепипеда с нестандартными размерами.
Предположим, что у нас есть параллелепипед с длиной стороны A = 8 см, шириной стороны B = 12 см и высотой C = 5 см.
Для начала необходимо вычислить площади каждой грани параллелепипеда. Всего у параллелепипеда шесть граней: по две грани противоположные и параллельные друг другу по каждому измерению: длине, ширине и высоте.
Площади граней в параллелепипеде вычисляются по формуле:
- Площадь грани, параллельной длине: S₁ = B * C = 12 см * 5 см = 60 см²
- Площадь грани, параллельной ширине: S₂ = A * C = 8 см * 5 см = 40 см²
- Площадь грани, параллельной высоте: S₃ = A * B = 8 см * 12 см = 96 см²
Таким образом, площадь каждой грани параллелепипеда равна:
- Грань, параллельная длине: S₁ = 60 см²
- Грань, параллельная ширине: S₂ = 40 см²
- Грань, параллельная высоте: S₃ = 96 см²
Общая площадь поверхности параллелепипеда равна сумме площадей всех его граней:
S = 2 * (S₁ + S₂ + S₃) = 2 * (60 см² + 40 см² + 96 см²) = 392 см².
Таким образом, площадь поверхности параллелепипеда с данными нестандартными размерами равна 392 см².
Преимущества использования формулы для вычисления площади поверхности
1. Точность: Формула для вычисления площади поверхности прямого параллелепипеда основана на точных геометрических принципах. Использование этой формулы гарантирует получение правильных и точных результатов.
2. Универсальность: Формула применима для любого прямого параллелепипеда, независимо от его размеров и пропорций. Это позволяет использовать формулу для вычисления площади поверхности любого объекта данной геометрической формы.
3. Простота использования: Формула для вычисления площади поверхности прямого параллелепипеда очень проста и легко запоминается. Она состоит из нескольких простых математических операций, таких как умножение и сложение, что позволяет осуществлять вычисления без особых усилий.
4. Эффективность: Использование формулы позволяет значительно сократить время, затрачиваемое на вычисление площади поверхности. Вместо ручных измерений и сложных геометрических конструкций, вы можете быстро и просто применить формулу и получить результат.
5. Гибкость: Формула позволяет экспериментировать с различными значениями размеров сторон параллелепипеда, изменять их и наблюдать, как это влияет на площадь поверхности. Благодаря этому, вы можете адаптировать формулу под любые условия и требования задачи.
Использование формулы для вычисления площади поверхности прямого параллелепипеда дает возможность быстро, точно и эффективно решать геометрические задачи, связанные с этой фигурой. Она является надежным математическим инструментом, который поможет вам получить точные результаты и избежать ошибок в расчетах.
Где использовать вычисление площади поверхности прямого параллелепипеда

Вычисление площади поверхности прямого параллелепипеда находит применение в различных сферах, где требуется работать с трехмерными объектами.
Строительство. В строительстве вычисление площади поверхности прямого параллелепипеда используется для определения необходимого объема материалов, таких как краска, обои или облицовочные плитки, для окрашивания стен или облицовки поверхностей.
Дизайн интерьера. Дизайнеры интерьера используют вычисление площади поверхности прямого параллелепипеда для оценки объема материалов, например, обоев, плитки или коврового покрытия, для планирования и оформления комнат.
Инженерия. В инженерии вычисление площади поверхности прямого параллелепипеда применяется для определения необходимого объема материалов, таких как бетон, стальные листы или пластик, для строительства и изготовления различных конструкций и оборудования.
Производство. В производственных процессах вычисление площади поверхности прямого параллелепипеда используется для оценки затрат и определения объема материалов, например, металла или пластика, необходимых для создания деталей и изделий.
Архитектура. Архитекторы используют вычисление площади поверхности прямого параллелепипеда для оценки объема материалов и планирования пространств внутри зданий.
Все эти области требуют точных вычислений площадей поверхностей прямых параллелепипедов для определения объема материалов, рассчета затрат и планирования пространств.
Формула для вычисления площади грани прямого параллелепипеда зависит от его формы. Для прямоугольника площадь грани вычисляется по формуле: П = 2a*b, где a и b - длины двух сторон прямоугольника. Для квадрата площадь грани равна: П = 4a^2, где a - длина стороны квадрата. Для равностороннего треугольника площадь грани рассчитывается по формуле: П = a^2*sqrt(3), где a - длина стороны треугольника.
Для вычисления общей площади поверхности параллелепипеда необходимо умножить площадь каждой его грани на 2 и сложить результаты. То есть, Поверхность = 2П1 + 2П2 + 2П3, где П1, П2, и П3 - площади граней параллелепипеда.
Пример вычисления площади поверхности прямого параллелепипеда:
- Дан прямоугольный параллелепипед с длиной сторон a = 5 см, b = 6 см и c = 4 см.
- Площадь каждой грани вычисляем по формуле: П1 = 2a*b = 2*5*6 = 60 см^2, П2 = 2b*c = 2*6*4 = 48 см^2, П3 = 2a*c = 2*5*4 = 40 см^2.
- общая площадь поверхности прямого параллелепипеда: Поверхность = 2П1 + 2П2 + 2П3 = 2*60 + 2*48 + 2*40 = 192 см^2.
Таким образом, площадь поверхности данного прямого параллелепипеда равна 192 см^2.