Прямоугольные треугольники – это особый вид треугольников, у которых один из углов равен 90 градусам. Их название говорит само за себя: эти треугольники имеют один прямой угол, а две другие стороны образуют прямой угол. Найти площадь прямоугольного треугольника не составляет особой сложности, если знать соответствующую формулу.
Формула нахождения площади прямоугольного треугольника состоит из двух частей: сначала необходимо найти длину одной из сторон треугольника, а затем умножить ее на высоту, опущенную на эту сторону.
Формула площади треугольника:
Площадь = (1/2) * сторона * высота
Здесь длина стороны указана перед высотой. Данная формула дает точное значение площади для прямоугольного треугольника.
Что такое прямоугольный треугольник?
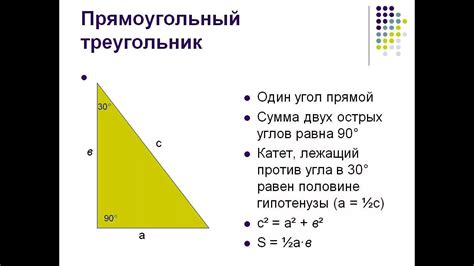
Прямоугольные треугольники широко применяются в геометрии и математике и являются основой для многих расчетов. Гипотенуза прямоугольного треугольника выступает в качестве главной диагонали прямоугольника, который можно построить на его сторонах. Уникальные свойства прямоугольных треугольников позволяют выполнять различные геометрические и алгебраические операции, включая нахождение площади треугольника.
Одним из способов определения площади прямоугольного треугольника является использование формулы: Площадь = (Катет_1 * Катет_2) / 2. В данной формуле, Катет_1 и Катет_2 обозначают длины катетов треугольника, которые являются прямыми сторонами, примыкающими к прямому углу.
Зачем нужно знать формулу площади прямоугольного треугольника?

- Решение геометрических задач: Зная формулу площади прямоугольного треугольника, вы сможете легко решать задачи, связанные с определением площади этого типа треугольника.
- Архитектурное проектирование: В архитектуре и строительстве знание формулы площади прямоугольного треугольника поможет рассчитать площадь крыши, орнамента или других деталей, имеющих эту форму.
- Геодезия и землемерие: При измерении участков земли или местности точное знание формулы площади прямоугольного треугольника позволяет быстро и безошибочно рассчитать площадь треугольного участка.
- Естественные науки: В физике и других естественных науках можно встретить ситуации, когда для определения площади требуется знание формулы площади прямоугольного треугольника. Например, при расчете площади теплопроводящей поверхности или гидродинамических задачах.
Таким образом, знание формулы площади прямоугольного треугольника является важным математическим инструментом, который может быть применен в различных областях. Оно поможет вам решать геометрические задачи, проводить измерения и рассчитывать площади фигур, имеющих эту форму.
Формула площади прямоугольного треугольника
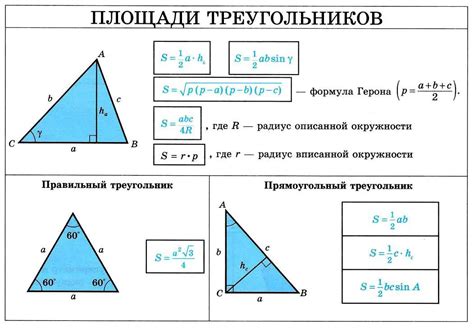
Формула для расчета площади прямоугольного треугольника запоминается очень просто:
S = (a * b) / 2
где S - площадь треугольника, a и b - длины катетов.
Для примера, рассмотрим треугольник с катетами длиной 5 и 8:
S = (5 * 8) / 2 = 40 / 2 = 20
Таким образом, площадь прямоугольного треугольника со сторонами 5 и 8 равна 20 квадратным единицам.
Какая формула позволяет найти площадь прямоугольного треугольника?

Площадь прямоугольного треугольника может быть найдена с помощью следующей формулы:
S = (a * b) / 2
Где:
- S - площадь треугольника.
- a - длина одного катета треугольника (стороны, образующие прямой угол).
- b - длина другого катета треугольника.
Таким образом, чтобы найти площадь прямоугольного треугольника, необходимо умножить длины обоих катетов и разделить полученное значение на 2.
Например, если длины катетов треугольника равны 6 и 8 единиц, то площадь треугольника будет:
S = (6 * 8) / 2 = 24
Итак, площадь прямоугольного треугольника в данном случае будет равна 24 единицам.
Какие данные необходимо знать для расчета площади треугольника?

Для расчета площади прямоугольного треугольника необходимо знать следующие данные:
- Длину одного катета треугольника - это сторона, которая является основанием для вычисления площади.
- Длину другого катета - вторая сторона, перпендикулярная к первому катету.
По этим данным можно применить формулу для нахождения площади прямоугольного треугольника, которая выглядит следующим образом:
S = (a * b) / 2
Где S - площадь треугольника, a - длина одного катета, b - длина другого катета.
Примеры расчета площади прямоугольного треугольника
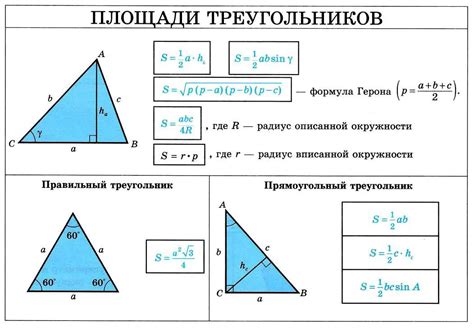
Рассмотрим несколько примеров:
Пример 1:
Дано:
Длина первого катета (a) = 5 см
Длина второго катета (b) = 8 см
Используя формулу, можем вычислить площадь:
S = (5 * 8) / 2 = 40 / 2 = 20 см²
Ответ: площадь прямоугольного треугольника равна 20 см².
Пример 2:
Дано:
Длина первого катета (a) = 12 м
Длина второго катета (b) = 9 м
Используя формулу, можем вычислить площадь:
S = (12 * 9) / 2 = 108 / 2 = 54 м²
Ответ: площадь прямоугольного треугольника равна 54 м².
Помните, что величина площади всегда будет иметь квадратные единицы измерения, так как это площадь.
Пример 1: Как найти площадь прямоугольного треугольника с известными катетами?

Шаг 1: Найдите значения длин двух катетов прямоугольного треугольника. Пусть длины катетов будут обозначены как a и b.
Шаг 2: Подставьте значения катетов в формулу площади прямоугольного треугольника: S = (a * b) / 2.
Шаг 3: Перемножьте значения катетов и разделите полученное число на 2. Результат будет площадью прямоугольного треугольника.
Пример: Пусть длина первого катета a равна 5 единицам, а длина второго катета b равна 7 единицам. Используя формулу площади, мы можем вычислить площадь треугольника:
S = (5 * 7) / 2 = 35 / 2 = 17.5
Таким образом, площадь прямоугольного треугольника с известными катетами длиной 5 и 7 единиц составляет 17.5 квадратных единиц.
Пример 2: Как найти площадь прямоугольного треугольника с известной гипотенузой и катетом?

Допустим, у вас есть прямоугольный треугольник, у которого известны длины гипотенузы и одного из катетов. Чтобы найти площадь такого треугольника, можно воспользоваться следующими шагами:
Шаг 1: Найдите длину второго катета, используя теорему Пифагора. Для этого можно воспользоваться формулой: катет^2 = гипотенуза^2 - известный катет^2.
Шаг 2: После того, как известны длины обоих катетов, можно применить формулу для вычисления площади прямоугольного треугольника: площадь = (длина первого катета * длина второго катета) / 2.
Давайте рассмотрим пример: у нас есть прямоугольный треугольник с гипотенузой длиной 10 единиц и известным катетом длиной 6 единиц.
Шаг 1: Используя теорему Пифагора, находим длину второго катета:
второй катет^2 = гипотенуза^2 - известный катет^2
второй катет^2 = 10^2 - 6^2
второй катет^2 = 100 - 36
второй катет^2 = 64
второй катет = 8
Шаг 2: Применяем формулу для вычисления площади прямоугольного треугольника:
площадь = (длина первого катета * длина второго катета) / 2
площадь = (6 * 8) / 2
площадь = 48 / 2
площадь = 24
Таким образом, площадь данного прямоугольного треугольника равна 24 единицам.
Пример 3: Как найти площадь прямоугольного треугольника с известным углом и одной стороной?

Площадь прямоугольного треугольника можно найти с помощью следующей формулы:
Площадь = (a * b) / 2
где a и b - это длины сторон прямоугольного треугольника, а Площадь - это искомое значение.
Представим ситуацию, когда известен один угол треугольника и длина одной из его сторон. Для решения данной задачи можно использовать тригонометрические функции. Рассмотрим пример:
Дано:
- Угол "α" равен 45 градусов.
- Длина стороны "a" равна 8 сантиметров.
Требуется найти площадь прямоугольного треугольника.
Решение:
- Отметим на плоскости точку "A", из которой будем проводить линии к двум другим точкам.
- Проведем сторону "a", образующую прямой угол с осью x.
- Из точки "A" проведем вторую сторону "b", образующую угол "α".
- Определим длину стороны "b" с помощью тригонометрической функции:
b = a * tan(α)
где "tan" - тангенс, "α" - угол, "a" - длина стороны.
Подставим значения из условия:
b = 8 * tan(45°) ≈ 8 * 1 ≈ 8
- Найдем площадь треугольника с помощью формулы:
Площадь = (a * b) / 2 = (8 * 8) / 2 = 32
Ответ: Площадь прямоугольного треугольника равна 32 квадратным сантиметрам.
Надеюсь, этот пример помог вам понять, как найти площадь прямоугольного треугольника с известным углом и одной стороной.
Важность знания формулы и методов расчета площади прямоугольного треугольника
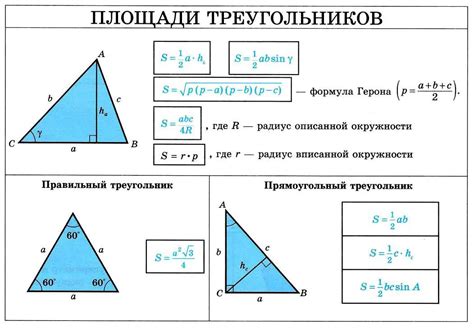
Формула для нахождения площади прямоугольного треугольника имеет простую структуру и основывается на знании длин двух его катетов. Нахождение площади треугольника может проводиться по формуле:
S = (a * b) / 2
Где S - площадь треугольника, a - длина одного из катетов, b - длина другого катета.
Знание данной формулы и методов ее применения позволяет легко и точно находить площадь прямоугольного треугольника и использовать эту информацию для решения геометрических задач.
Например, зная площадь прямоугольного треугольника и один из катетов, можно легко вычислить длину другого катета. Также, на основе площади и длины одного из катетов, можно решать задачи с заданными условиями на нахождение высоты, периметра и других характеристик треугольника.
Изучение и применение формулы и методов расчета площади прямоугольного треугольника помогают развивать логическое мышление, улучшают навыки решения задач и позволяют лучше понимать принципы геометрии. Поэтому важно уделять достаточно внимания изучению данной темы, чтобы быть готовым к решению практических задач.
Как применить полученные знания в практических задачах?

Понимание формулы для расчета площади прямоугольного треугольника может быть полезно во множестве практических задач. Рассмотрим некоторые из них:
1. Расчет площади участка земли:
Если имеется участок земли, который имеет форму прямоугольного треугольника, зная длину основания и высоту, можно легко рассчитать его площадь. Это может быть полезно при планировании земельного участка или подсчете площади садового участка.
2. Расчет площади крыши:
В случае, когда крыша здания имеет форму прямоугольного треугольника, можно использовать формулу для расчета площади. Это может быть полезно при проектировании крыши или рассчете материалов для ее строительства.
3. Определение площади фигур на плоскости:
Зная, что треугольник со сторонами a, b и гипотенузой c является прямоугольным, можно легко рассчитать площадь этого треугольника. Это может быть полезно при расчете площади различных геометрических фигур на плоскости.
Это лишь некоторые примеры практического применения расчета площади прямоугольного треугольника. В реальной жизни могут возникать самые разнообразные задачи, в которых знание данной формулы позволит решить проблему эффективно и точно.