Равнобедренный треугольник – это треугольник, у которого две стороны равны друг другу. Он является одним из основных типов треугольников и имеет много применений в геометрии, физике, строительстве и других областях. Особенностью равнобедренных треугольников является то, что они имеют два равных угла и один неравный, который называется основанием.

Для определения площади равнобедренного треугольника применяется специальная формула, основанная на свойствах этого типа треугольников. Она позволяет быстро и легко вычислить площадь треугольника, зная только его высоту, которая является перпендикуляром, опущенным из вершины треугольника на основание.

Формула для вычисления площади равнобедренного треугольника записывается следующим образом: S = (1/2) * a * h, где a – длина одной из сторон треугольника (сторона-основание), h – высота треугольника.

Если у вас нет данных о высоте, вы можете использовать другую формулу, которая связывает площадь равнобедренного треугольника с длинами его сторон и углом между ними: S = (1/4) * √(4 * a^2 - b^2) * √(b^2 - a^2 * cos^2α), где a – длина стороны треугольника (сторона-основание), b – длина одной из равных сторон, α – угол между стороной-основанием и одной из равных сторон.

Расчет площади равнобедренного треугольника

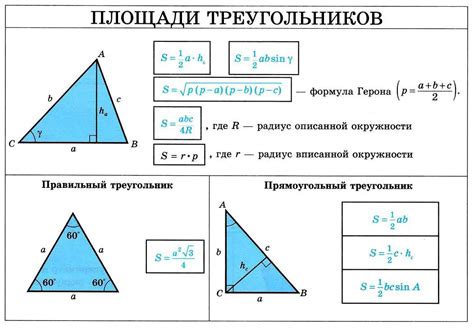
Для начала, необходимо знать значение длины основания и высоты равнобедренного треугольника. Основанием является одна из сторон треугольника, а высота – перпендикуляр, опущенный из вершины к основанию.

Площадь равнобедренного треугольника можно вычислить по формуле:

S = (b * h) / 2

где S – площадь, b – длина основания, а h – высота.

Равнобедренный треугольник имеет две равные стороны и две равные углы, поэтому основание можно найти путем деления периметра на 2:

b = P / 2

где P – периметр.

Чтобы найти высоту равнобедренного треугольника, можно использовать теорему Пифагора:

h = sqrt(a^2 - (b/2)^2)

где a – длина боковой стороны (равная двум другим сторонам).

После определения длины основания и высоты, можно подставить их значения в формулу для площади треугольника и вычислить итоговую площадь.

Таким образом, расчет площади равнобедренного треугольника основывается на знании длины основания и высоты, а также применении соответствующих формул. Этот метод позволяет быстро и легко определить площадь равнобедренного треугольника.

Формула для определения площади равнобедренного треугольника

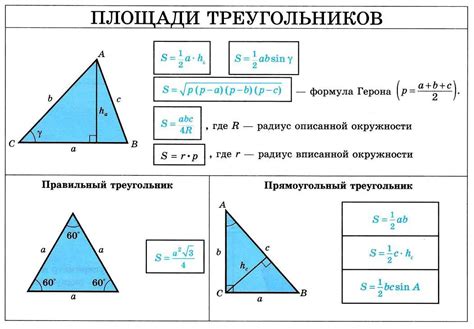
Формула для определения площади равнобедренного треугольника имеет следующий вид:

S = (a^2 * √(4 * b^2 - a^2)) / 4

Где:

• S - площадь треугольника
• a - длина основания треугольника
• b - длина боковой стороны треугольника

Для использования этой формулы необходимо знать длину основания и одной из боковых сторон равнобедренного треугольника. Подставляя значения в формулу и выполняя вычисления, можно определить площадь треугольника.

Например, если длина основания треугольника равна 10 см, а длина боковой стороны равна 8 см, то площадь можно определить следующим образом:

S = (10^2 * √(4 * 8^2 - 10^2)) / 4 = (100 * √(256 - 100)) / 4 = (100 * √156) / 4 ≈ 100 * 12.49 / 4 ≈ 1250 / 4 ≈ 312.5

Таким образом, площадь равнобедренного треугольника с основанием 10 см и боковой стороной 8 см равна примерно 312.5 квадратных сантиметров.