Ромб – это четырехугольник, у которого все стороны равны друг другу. Это позволяет найти его площадь с помощью простой формулы, которая выражает площадь ромба через длину его диагоналей. Если ты хочешь рассчитать площадь ромба или решить задачу, связанную с этой фигурой, здесь ты найдешь все необходимые формулы и примеры решения задачи.
Для начала, узнаем, что диагональ – это отрезок, соединяющий две противоположные вершины ромба. У ромба есть две диагонали: большая и меньшая. Обозначим большую диагональ как Д1, а меньшую – как Д2. Длины диагоналей обозначим соответственно как а и в.
Теперь мы готовы к формуле для нахождения площади с ромба:
S = (Д1 * Д2) / 2
Зная длины диагоналей, мы можем подставить их значения в формулу и получить площадь S ромба. Давай рассмотрим примеры решения задачи:
Что такое площадь ромба и как ее найти?

S = d1 * d2 / 2
где S - площадь ромба, d1 и d2 - диагонали ромба.
Для нахождения площади ромба, необходимо знать длины его диагоналей. Если диагонали известны, то они подставляются в формулу и выполняется вычисление.
Пример:
- Пусть диагонали ромба равны 8 см и 6 см.
- Умножаем длины диагоналей:
- 8 см * 6 см = 48 см²
- Делим этот результат на 2:
- 48 см² / 2 = 24 см²
- Площадь ромба равна 24 см².
Таким образом, площадь ромба составляет 24 квадратных сантиметра.
Формула площади ромба с примером вычисления
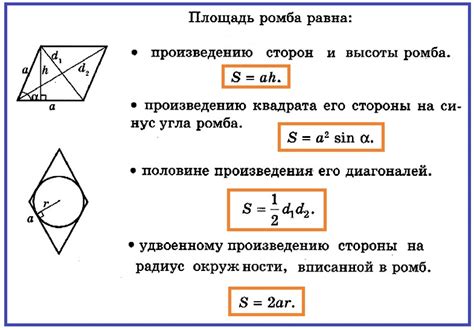
Площадь ромба можно вычислить, зная длины его диагоналей. Для этого применяется следующая формула:
S = (d1 * d2) / 2
где S - площадь ромба, d1 и d2 - диагонали ромба.
Для наглядности рассмотрим пример вычисления площади ромба:
Пример 1:
- Пусть d1 = 8 см и d2 = 6 см.
- Подставим значения в формулу: S = (8 * 6) / 2 = 24 см².
- Ответ: площадь ромба равна 24 см².
Пример 2:
- Пусть d1 = 12 м и d2 = 10 м.
- Подставим значения в формулу: S = (12 * 10) / 2 = 60 м².
- Ответ: площадь ромба равна 60 м².
Таким образом, зная длины диагоналей ромба, можно легко вычислить его площадь по формуле (d1 * d2) / 2.
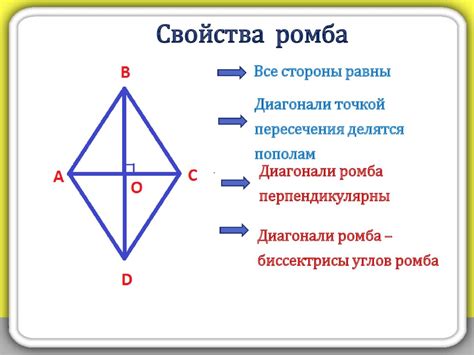
Свойства ромба, влияющие на его площадь
| Свойство | Описание |
|---|---|
| Диагонали | Для ромба характерно то, что его диагонали пересекаются в точке, деля ее пополам. Длина диагоналей является основным параметром при вычислении площади ромба. |
| Высота | Высота ромба - это отрезок, проведенный из любой вершины ромба перпендикулярно противоположной стороне. Высота также является ключевым показателем при расчете площади. |
| Углы | У каждого ромба все углы равны между собой, поэтому один из углов может быть легко вычислен. Для вычисления площади ромба угол является необходимой информацией. |
Для вычисления площади ромба можно использовать различные формулы, включающие данные свойства. Наиболее распространенной формулой для вычисления площади ромба является:
Площадь = (длина первой диагонали * длина второй диагонали) / 2
Для расчета площади ромба можно также использовать другие формулы, основанные на высоте и угле. Важно помнить, что все показатели должны быть выражены в одних и тех же единицах измерения.
Используя эти свойства и соответствующие формулы, можно легко вычислить площадь ромба, что поможет в решении задач и понимании геометрических принципов, связанных с этой фигурой.
Практические примеры решения задач на нахождение площади ромба

Рассмотрим несколько практических примеров решения задач на нахождение площади ромба:
Пример 1:
Дан ромб со стороной длиной 6 см и высотой, опущенной на одну из сторон, равной 4 см. Найдем площадь этого ромба.
Решение:
Для нахождения площади ромба можно воспользоваться формулой: S = (a * h), где S – площадь ромба, a – длина стороны, h – длина высоты, опущенной на сторону.
В нашем примере площадь ромба будет равна: S = (6 см * 4 см) = 24 см².
Ответ: площадь ромба равна 24 квадратных сантиметра.
Пример 2:
Дан ромб со стороной длиной 10 см и высотой, опущенной на одну из сторон, равной 8 см. Найдем площадь этого ромба.
Решение:
Используем формулу для нахождения площади ромба: S = (a * h).
Подставляем значения: S = (10 см * 8 см) = 80 см².
Ответ: площадь ромба равна 80 квадратных сантиметров.
Таким образом, решая задачи на нахождение площади ромба, необходимо знать длину стороны и длину высоты, на которую опущена эта сторона. Пользуясь формулой S = (a * h), можно легко решить задачи и найти площадь ромба.