Ромб - это выглядящая как четырехугольник фигура, у которой все стороны равны. Это очень интересная геометрическая фигура, которая имеет свои уникальные свойства и характеристики.

Если вам нужно найти площадь ромба, то это совсем несложно! Нужно всего лишь знать несколько формул и следовать простым шагам.

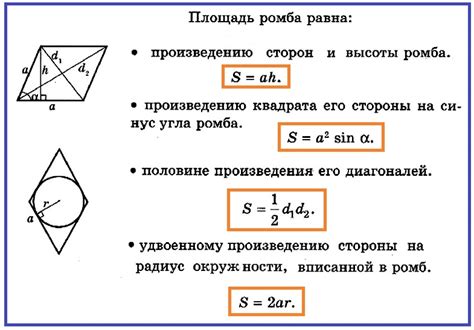
Формула для нахождения площади ромба звучит так: S = e * h.

Где e - это любая из сторон ромба, а h - это высота, которая может быть найдена как прямая линия, проходящая через середину ромба и перпендикулярная двум противоположным сторонам.

Как вычислить площадь ромба простым способом

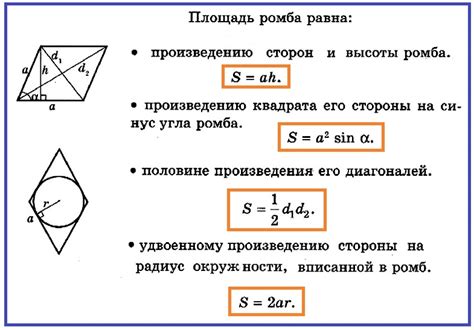
Чтобы найти площадь ромба, необходимо знать длину его диагоналей. Обозначим эти диагонали буквами d₁ и d₂. Тогда формула для вычисления площади равна:

S = (d₁ * d₂) / 2

Для упрощения вычислений можно заметить, что длина любой диагонали ромба является высотой его равнобедренного треугольника, а основаниями этого треугольника являются стороны ромба.

Таким образом, площадь ромба можно вычислить, зная длину одной из его сторон и высоту (длину диагонали). Формула для этого случая:

S = a * h,

где a – длина одной из сторон, h – длина диагонали (высота).

Теперь, зная простые способы вычисления площади ромба, вы можете легко решать задачи, связанные с этимы фигурами.

Формула нахождения площади ромба

Площадь ромба = (длина диагонали 1 * длина диагонали 2) / 2

Где:

• Длина диагонали 1 - это расстояние между двумя противоположными вершинами ромба.
• Длина диагонали 2 - это расстояние между двумя другими противоположными вершинами ромба, перпендикулярное диагонали 1.

Пример вычисления площади ромба:

Пусть длина диагонали 1 равна 10 см, а длина диагонали 2 равна 6 см.

Площадь ромба = (10 * 6) / 2 = 30 см²

Таким образом, площадь ромба с данными длинами диагоналей равна 30 квадратным сантиметрам.

Пример вычисления площади ромба для 9 класса

Рассмотрим пример вычисления площади ромба на конкретном числовом значении стороны.

Пусть дан ромб ABCD со стороной равной 6 см. Для начала найдем высоту ромба, проведя отрезок, соединяющий середины двух противоположных сторон. По свойству ромба, этот отрезок будет равен высоте ромба.

Используем формулу площади треугольника: S = (a * h) / 2, где a - длина одной стороны треугольника, h - высота, проведенная к этой стороне.

Так как сторона ромба равна 6 см, то длина боковых сторон треугольника, образованного высотой ромба, будет равна 6 см.

Высота ромба равна половине длины диагонали, поэтому для нахождения высоты ромба потребуется найти длину диагонали внутри ромба.

Рассмотрим треугольник ADB, для которого известны стороны AD = 6 см, DB = 6 см и угол между этими сторонами равен 90 градусов.

Используем теорему Пифагора для нахождения длины диагонали: сумма квадратов катетов равна квадрату гипотенузы. В нашем случае AD и DB - это катеты, а диагональ и прямоугольник ADB - гипотенуза.

AD^2 + DB^2 = AB^2

6^2 + 6^2 = AB^2

36 + 36 = AB^2

72 = AB^2

AB = √72

Находим длину диагонали AB = √72 = 8.485 см.

Теперь находим высоту ромба, которая равна половине длины диагонали: h = AB / 2 = 8.485 / 2 = 4.242 см.

Подставляем значения в формулу площади треугольника: S = (a * h) / 2 = (6 * 4.242) / 2 = 25.452 / 2 = 12.726 см².

Таким образом, площадь ромба ABCD со стороной 6 см равна 12.726 см².