Ромб - это четырехугольник, у которого все стороны равны между собой. Особенностью ромба является то, что он имеет равные диагонали, которые пересекаются в центре ромба под прямым углом.
Для нахождения площади ромба необходимо знать длину одной из его сторон и длину одной из его диагоналей. Формула нахождения площади ромба довольно проста:
Площадь ромба (S) равна половине произведения длин его диагоналей (d1 и d2):
S = (d1 * d2) / 2
Для более точного результата рекомендуется записывать значения диагоналей ромба в одних и тех же единицах измерения, например, сантиметрах или метрах.
Теперь, когда вы знаете формулу для нахождения площади ромба, вы можете легко решать геометрические задачи и получать точные результаты.
Что такое ромб и его особенности
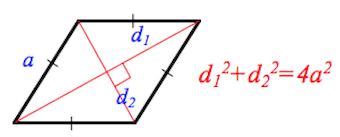
- Все углы в ромбе равны между собой. Ромб является ромбом, если он имеет четыре угла по 90 градусов.
- Диагонали ромба делят его на четыре равных треугольника. Это значит, что углы между диагоналями и сторонами ромба также равны.
- Два соседних угла в ромбе образуют линию, которая называется диагональным углом. Диагональный угол ромба всегда равен 180 градусов минус угол ромба.
- Высота ромба - это расстояние между противоположными сторонами. Высота всегда перпендикулярна этим сторонам.
Теперь, когда мы знаем основные характеристики ромба, мы можем использовать соответствующую формулу для вычисления его площади. Формула для площади ромба: S = d1 * d2 / 2, где d1 и d2 - длины диагоналей ромба.
Используя эту формулу, вы можете легко найти площадь ромба, зная длины его диагоналей. Таким образом, ромб - это уникальная геометрическая фигура с интересными свойствами и измерениями. Знание этих особенностей поможет вам лучше понять и решать задачи, связанные с ромбами.
Ромб - геометрическая фигура с четырьмя равными сторонами
Ромб имеет несколько интересных свойств. Во-первых, диагонали ромба делят его на четыре равные треугольные части. Во-вторых, диагонали ромба перпендикулярны друг другу и пересекаются в центре ромба. В-третьих, площадь ромба можно вычислить, зная длину его диагоналей.
Формула для вычисления площади ромба:
- Выберите одну из диагоналей ромба и обозначьте ее как d1.
- Выберите другую диагональ и обозначьте ее как d2.
- Умножьте длину диагонали d1 на длину диагонали d2.
- Результат умножьте на 0.5.
Таким образом, формула для вычисления площади ромба будет следующей:
Площадь = (d1 * d2) * 0.5
Где d1 и d2 - длины диагоналей ромба.
Используя эту формулу, вы можете легко вычислить площадь ромба, если известны длины его диагоналей. Это может быть полезно при решении задач на нахождение площади ромба, например, при построении или измерении поверхности ромбообразного объекта.
Формула для вычисления площади ромба
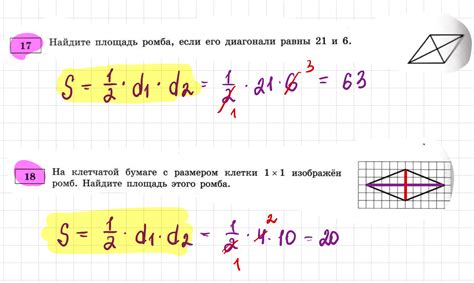
Формула для вычисления площади ромба основана на длинах его сторон и угла между ними. Для этого вначале нужно найти продукт длин диагоналей и разделить его на 2:
| Площадь ромба (S) = | 1/2 | × | (a × b) |
где:
- (a) и (b) - длины диагоналей ромба
Таким образом, чтобы вычислить площадь ромба, необходимо узнать длины его диагоналей и подставить их значения в формулу.
Площадь ромба равна произведению диагоналей на половину их суммы

Зная значения длин диагоналей, можно легко рассчитать площадь ромба. Для этого необходимо умножить длины диагоналей и разделить полученное произведение на 2.
| Ромб | Диагонали | Площадь |
|---|---|---|
| d1 - длина диагонали AC | S = (d1 * d2) / 2 |
| d2 - длина диагонали BD |
Найдем площадь ромба для примера:
| Ромб | Диагонали | Площадь |
|---|---|---|
| d1 = 8 см | S = (8 * 10) / 2 = 40 см² |
| d2 = 10 см |
Таким образом, площадь данного ромба составляет 40 см².
Примеры расчета площади ромба:
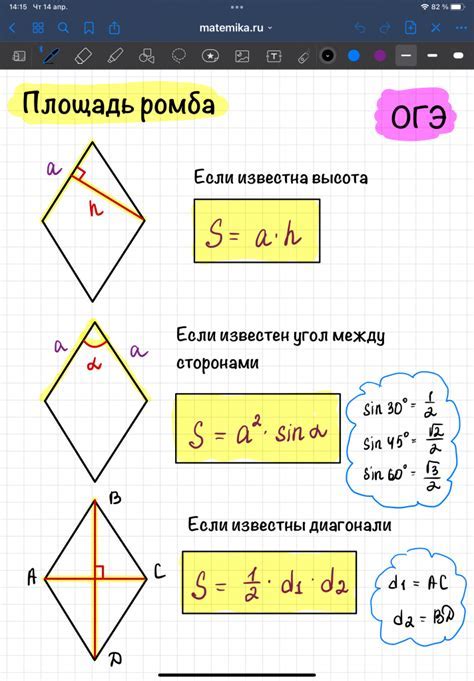
Для нахождения площади ромба можно использовать две разные формулы, в зависимости от известной информации о фигуре.
1. Если известны длины диагоналей ромба:
- Найдите значение одной из диагоналей ромба.
- Умножьте значение найденной диагонали на другую диагональ и разделите полученное произведение на 2.
- Полученное число будет являться площадью ромба.
2. Если известна длина стороны ромба:
- Возвести значение длины стороны ромба в квадрат.
- Умножьте полученное значение на синус угла между стороной ромба и осью симметрии.
- Полученное число будет являться площадью ромба.
Например, для ромба с известными длинами диагоналей 6 и 8:
- Найдем значение одной из диагоналей, например, 6.
- Умножим значение диагонали на другую диагональ и разделим полученное произведение на 2: 6 * 8 / 2 = 24.
- Площадь ромба равна 24 квадратных единиц.
А для ромба со стороной длиной 5 и углом 45 градусов между стороной и осью симметрии:
- Возведем длину стороны в квадрат: 5 * 5 = 25.
- Умножим полученное значение на синус угла 45 градусов: 25 * sin(45) ≈ 17.68.
- Площадь ромба примерно равна 17.68 квадратных единиц.