Трапеция – это геометрическая фигура, которая имеет две параллельные стороны и две непараллельные стороны. На координатной плоскости трапеция может быть представлена точками с координатами, и для нахождения ее площади можно использовать геометрические и алгебраические методы.

Для подсчета площади трапеции на координатной плоскости воспользуемся формулой, основанной на нахождении высоты и средней линии. Сначала необходимо найти длину оснований трапеции, затем найти длину высоты, перпендикулярной основаниям. Зная значения этих величин, можно применить формулу для нахождения площади:

S = ((a + b) * h) / 2

где a и b – длины оснований, а h – длина высоты трапеции. Подставив известные значения, можно вычислить площадь.

Для лучшего понимания и закрепления материала рассмотрим примеры. Представим, что имеется трапеция с основаниями длиной 6 и 4, а высота равна 3. Применив формулу для вычисления площади, получим:

S = ((6 + 4) * 3) / 2 = 15

Таким образом, площадь данной трапеции равна 15.

Определение площади трапеции

Формула для нахождения площади трапеции: S = (a + b) * h / 2, где a и b - длины оснований, h - высота трапеции.

Чтобы найти площадь трапеции на координатной плоскости, нужно знать координаты ее вершин. Для этого можно использовать координаты четырех точек: A(x1, y1), B(x2, y2), C(x3, y3) и D(x4, y4), где точки A и B - вершины одного основания, а точки C и D - вершины другого основания.

Для вычисления площади трапеции находим расстояние между точками A и B, а затем умножаем его на среднее арифметическое значение y-координат точек C и D.

Пример:

Даны координаты вершин трапеции: A(2, 4), B(8, 4), C(6, 2) и D(4, 2).

Расстояние между точками A и B равно 8 единиц (8 - 2).

Среднее арифметическое значение y-координат точек C и D равно 2 (2 + 2) / 2.

Тогда площадь трапеции вычисляется по формуле: S = 8 * 2 / 2 = 8 квадратных единиц.

Таким образом, площадь заданной трапеции равна 8 квадратных единиц.

Координатная плоскость

Для обозначения точек на координатной плоскости используется система декартовых координат. Точка задается двумя числами в виде (x, y), где x - горизонтальная координата (абсцисса), y - вертикальная координата (ордината).

При построении фигур на координатной плоскости используются различные геометрические фигуры, такие как линии, окружности, многоугольники и трапеции. Они могут быть определены с помощью координат точек, через которые они проходят.

Используя координатную плоскость, вы можете легко рассчитать площадь фигур, таких как трапеция. Необходимо знать координаты вершин трапеции и применить соответствующую формулу расчета площади.

Где b1 и b2 - длины параллельных сторон трапеции, h - высота трапеции (расстояние между параллельными сторонами). Просто подставьте значения в формулу и рассчитайте площадь.

Координаты точек на плоскости

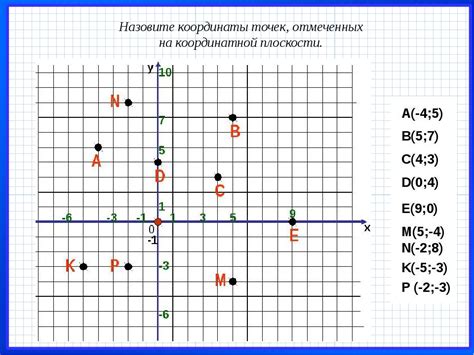
Координатные оси образуют систему координат, в которой точка (0, 0) называется началом координат. Абсцисса и ордината увеличиваются вправо и вверх соответственно.

При работе с трапециями на координатной плоскости, для определения координат точек необходимо знать их положение относительно осей координат.

Например, для трапеции с координатами вершин A(x1, y1), B(x2, y2), C(x3, y3) и D(x4, y4), можно определить положение вершины A относительно осей координат следующим образом:

• Если x1 > 0 и y1 > 0, то вершина A находится в первой четверти;
• Если x1 0, то вершина A находится во второй четверти;
• Если x1
• Если x1 > 0 и y1
• Если x1 = 0 и y1 = 0, то вершина A находится в начале координат.

Аналогично можно определить положение остальных вершин трапеции относительно осей координат.

Знание координат точек на плоскости позволяет проводить вычисления и строить графики различных фигур, включая трапеции.

Построение трапеции на координатной плоскости

Для построения трапеции на координатной плоскости необходимо знать координаты ее вершин. Трапеция образуется четырьмя точками, которые можно обозначить как A(x1, y1), B(x2, y2), C(x3, y3) и D(x4, y4).

Чтобы построить трапецию, следуйте следующим шагам:

1. Найдите координаты каждой вершины трапеции.
2. На координатной плоскости отметьте эти четыре точки.
3. Соедините точки линиями, чтобы получить фигуру трапеции.

Пример:

Допустим, мы имеем трапецию с вершинами A(-2, 1), B(4, 1), C(3, 5) и D(0, 5). Чтобы построить эту трапецию:

1. На координатной плоскости отметьте точки A(-2, 1), B(4, 1), C(3, 5) и D(0, 5).
2. Соедините эти точки линиями: AB, BC, CD и DA.

Теперь у вас есть построенная трапеция на координатной плоскости.

Используя эти шаги, вы сможете построить любую трапецию на координатной плоскости, зная координаты ее вершин.

Формула площади трапеции

Площадь трапеции можно рассчитать с помощью следующей формулы:

S = 0,5 * (a + b) * h,

где

• S - площадь трапеции;
• a и b - основания трапеции (длины сторон, параллельных друг другу);
• h - высота трапеции (расстояние между основаниями).

Важно отметить, что основания трапеции должны быть параллельны. Если они не параллельны, необходимо использовать другую формулу для рассчета площади.

Для примера рассмотрим трапецию со сторонами a = 5, b = 9 и высотой h = 4. Подставим значения в формулу:

S = 0,5 * (5 + 9) * 4

S = 0,5 * 14 * 4

S = 7 * 4

S = 28

Таким образом, площадь данной трапеции равна 28 квадратных единиц.

Используя данную формулу и известные значения, вы сможете легко рассчитать площадь трапеции на координатной плоскости.

Примеры расчета

Приведем несколько примеров расчета площади трапеции на координатной плоскости:

Пример 1:

Даны координаты четырех точек: A(1, 2), B(4, 5), C(7, 2), D(2, 2).

Для начала, найдем длины оснований трапеции AB и CD:

AB = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(4 - 1)² + (5 - 2)²] = √(3² + 3²) = √18 ≈ 4.24

CD = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(2 - 7)² + (2 - 2)²] = √((-5)² + 0²) = √25 = 5

Зная длины оснований и высоту h = |y₂ - y₁|, можно вычислить площадь трапеции по формуле:

S = ((AB + CD) / 2) * h = ((4.24 + 5) / 2) * 3 = 23.7

Ответ: площадь трапеции равна 23.7 квадратных единиц.

Пример 2:

Даны координаты четырех точек: A(-3, 4), B(2, 4), C(2, -1), D(-3, -1).

Найдем длины оснований трапеции AB и CD:

AB = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(2 - (-3))² + (4 - 4)²] = √(5² + 0²) = 5

CD = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(-3 - 2)² + (-1 - (-1))²] = √((-5)² + 0²) = √25 = 5

Зная длины оснований и высоту h = |y₂ - y₁|, можно вычислить площадь трапеции:

S = ((AB + CD) / 2) * h = ((5 + 5) / 2) * 5 = 25

Ответ: площадь трапеции равна 25 квадратных единиц.

Пример 3:

Даны координаты четырех точек: A(-1, -2), B(3, 5), C(5, 5), D(2, -2).

Длины оснований трапеции AB и CD:

AB = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(3 - (-1))² + (5 - (-2))²] = √(4² + 7²) = √(16 + 49) = √65 ≈ 8.06

CD = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(2 - 5)² + (-2 - 5)²] = √((-3)² + (-7)²) = √(9 + 49) = √58 ≈ 7.62

Высота трапеции h = |y₂ - y₁| = |5 - (-2)| = 7

Площадь трапеции вычисляется по формуле:

S = ((AB + CD) / 2) * h = ((8.06 + 7.62) / 2) * 7 = 53.45

Ответ: площадь трапеции равна 53.45 квадратных единиц.

Особенности расчета наложенных трапеций

Расчет площади наложенных трапеций на координатной плоскости может быть сложной задачей. В отличие от обычных трапеций, наложенные трапеции имеют сложную структуру и требуют специального подхода при расчете.

Для расчета площади наложенных трапеций необходимо разделить фигуру на отдельные трапеции и вычислить площадь каждой из них. Затем, полученные значения суммируются, чтобы получить общую площадь фигуры.

При расчете площади наложенных трапеций важно учесть, что каждая отдельная трапеция может иметь разные размеры и углы. Необходимо измерить длину каждой стороны и угол между ними для каждой трапеции. Затем, используя формулу для площади трапеции, можно вычислить площадь каждой отдельной трапеции и общую площадь наложенных фигур.

Также следует обратить внимание на выбор системы координат при расчете площади наложенных трапеций. Если требуется вычислить площадь наложенных трапеций на декартовой плоскости, то можно использовать обычную систему координат.

Важность проверки результатов

Во время решения задачи необходимо следить за каждым этапом расчета. Операции с числами, перестановка координат точек, а также другие действия могут содержать потенциальные ошибки. Проверяйте каждый результат на соответствие ожидаемому ответу и сравнивайте их с другими методами нахождения площади.

Ошибки при нахождении площади трапеции можно исправить путем:

• Проверки правильности подсчета координат точек.
• Сравнения полученного результата с другими методами поиска площади трапеции.
• Использования формулы для нахождения площади трапеции и последующей проверки найденного значения.