Площадь треугольника - это одно из важнейших понятий геометрии, с которым знакомят детей уже на самых ранних этапах обучения. В этой статье мы расскажем о простых методах нахождения площади треугольника, которые подходят для учеников 3 класса. Познакомимся с основными понятиями и легкими способами расчета!
Наша статья призвана помочь маленьким ученикам легко и быстро находить площадь треугольников. Наши простые методы подойдут даже для детей, только начинающих изучать геометрию. Мы научим их использовать формулы, которые легко запомнить и применять.
Основная формула для вычисления площади треугольника - это "половина произведения основания на высоту". При использовании данной формулы важным условием является знание основания и высоты треугольника. Расчет площади треугольника маленького размера можно выполнить в уме, а для более сложных треугольников можно использовать линейку и математический набор.
Что такое площадь треугольника
Треугольник - это геометрическая фигура, состоящая из трех отрезков, называемых сторонами треугольника, и трех точек, в которых эти стороны пересекаются, называемых вершинами треугольника.
Площадь треугольника - это мера, которая выражает размер плоского пространства, занимаемого треугольником.
Измерение площади треугольника имеет большое значение в геометрии и позволяет определить его понятия, такие как периметр и углы. Знание площади треугольника помогает нам понять и решать различные задачи, связанные с этой фигурой.
Определение площади треугольника
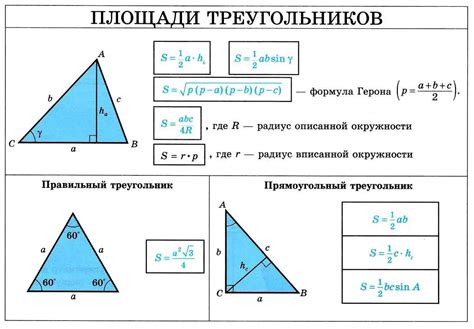
Определить площадь треугольника можно разными способами, например, с использованием формулы, зная значения длин сторон треугольника. Для этого можно воспользоваться формулой Герона или формулой полупериметра.
Формула Герона:
Площадь треугольника равна квадратному корню из произведения полупериметра треугольника и разности полупериметра и длин сторон треугольника.
Формула полупериметра:
Для определения полупериметра треугольника нужно сложить длины его сторон и разделить полученную сумму на 2.
Количество способов определения площади треугольника может быть больше, но эти две формулы являются основными и простыми для использования в начальной школе. При использовании этих формул необходимо учитывать правильное округление значений для получения точного результата.
Формула площади треугольника через основание и высоту
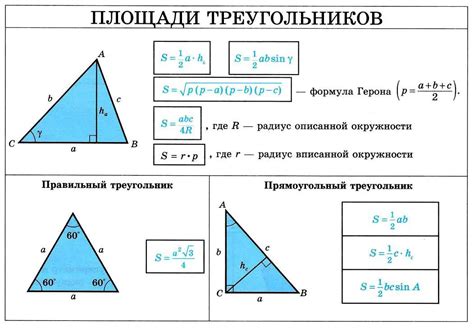
Если у нас есть треугольник с заданным основанием и высотой, мы можем использовать простую формулу для нахождения его площади. Формула гласит:
Площадь треугольника равна половине произведения его основания и высоты:
S = (a * h) / 2
Где S - площадь, a - основание треугольника и h - высота треугольника.
Метод Герона для определения площади треугольника
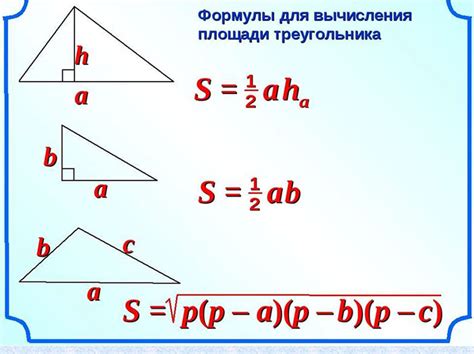
Для применения метода Герона необходимо знать длины всех трех сторон треугольника - a, b и c. Площадь треугольника можно вычислить, используя формулу:
S = sqrt(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, p - полупериметр треугольника, равный (a + b + c) / 2.
Используя формулу и зная длины сторон треугольника, можно легко вычислить его площадь. Например, если длины сторон треугольника равны a = 5, b = 4 и c = 3, то:
p = (a + b + c) / 2 = (5 + 4 + 3) / 2 = 6.
Теперь мы можем подставить значения в формулу:
S = sqrt(6 * (6 - 5) * (6 - 4) * (6 - 3)) = sqrt(6 * 1 * 2 * 3) = sqrt(36) = 6.
Таким образом, площадь треугольника с заданными сторонами равна 6 квадратным единицам.
Метод Герона является простым и эффективным способом определения площади треугольника на основе его сторон. Он может быть использован учащимися 3 класса для решения задач на определение площади треугольника.