Квадрат и треугольник - две из самых распространенных и простых геометрических фигур. Но что делать, если нужно найти площадь треугольника, который можно вписать в квадрат? В этой статье мы покажем тебе, как это сделать!
Для начала, давай познакомимся с основными формулами, которые понадобятся нам для решения этой задачи. Площадь квадрата вычисляется по формуле: S = a², где а - длина стороны квадрата. А площадь треугольника можно найти по формуле: S = 0.5 * a * h, где а - длина основания треугольника, а h - высота треугольника.
Уже можно догадаться, что для нахождения площади треугольника из квадрата нам нужно найти значения стороны квадрата и длины основания треугольника. Так как треугольник вписан в квадрат, то сторона квадрата равна длине его диагонали, а основание треугольника равно двум сторонам квадрата. Выглядит просто, не так ли?
Один из способов нахождения площади треугольника из квадрата

Площадь треугольника можно найти разными способами. Один из них предполагает использование квадрата.
Допустим, у нас есть квадрат со стороной a. Вершины квадрата обозначим буквами: A, B, C и D.
Чтобы найти площадь треугольника, нужно взять любые две вершины и провести диагональ квадрата, соединяющую эти вершины. Таким образом, получится два треугольника: ABP и BCP, где P - точка пересечения диагоналей квадрата.
Так как квадрат является фигурой с равными сторонами и прямыми углами, треугольники ABP и BCP будут равновеликими. Соответственно, площадь треугольника ABP будет равна площади треугольника BCP.
Площадь треугольника равна половине произведения его основания на высоту. Так как мы знаем, что сторона квадрата равна a, то основание треугольников равно a. Нам нужно найти высоту одного из этих треугольников.
Обратимся к диагоналям квадрата. По теореме Пифагора квадрат длины диагонали равен сумме квадратов сторон квадрата.
Тогда, с использованием теоремы Пифагора, можем найти длину диагонали по формуле .
Теперь мы можем найти высоту треугольника, проведенную к основанию. По свойству равнобедренных треугольников, проведенная к основанию является медианой и делит основание пополам. То есть, высота равна половине стороны треугольника, т.е. a/2.
Таким образом, площадь каждого из треугольников равна половине произведения a на a/2, или, в итоге, a2/4.
Поскольку площадь треугольника ABP и треугольника BCP равны, их суммарная площадь будет равна удвоенной площади одного из них, т.е. a2/2.
Итак, мы нашли способ нахождения площади треугольника из квадрата, который составляет половину площади квадрата.
| Квадрат | Треугольник ABP | Треугольник BCP |
|---|---|---|
 |  |  |
Формула для вычисления площади треугольника
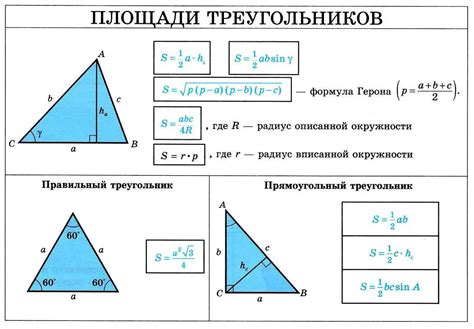
Площадь любого треугольника можно вычислить, зная длины основания и высоты треугольника. Существует формула, которая позволяет найти площадь треугольника, используя эти два параметра:
1. Найдите длину основания треугольника.
2. Найдите высоту треугольника.
3. Перемножьте длину основания на высоту и разделите полученное значение пополам.
Таким образом, формула для вычисления площади треугольника выглядит следующим образом:
Площадь = (длина основания * высота) / 2
Например, если основание треугольника равно 4 единицы, а высота равна 6 единицам, то площадь будет равна (4 * 6) / 2 = 12 единиц квадратных.
Используя данную формулу, вы сможете легко вычислить площадь треугольника, зная значения основания и высоты.
Способ вычисления площади квадрата

Площадь квадрата можно вычислить, зная длину его стороны, по формуле:
Площадь = сторона × сторона
При этом все стороны квадрата равны между собой, поэтому формулу можно упростить:
Площадь = сторона²
Например, если длина стороны квадрата равна 5 см, то площадь составит:
Площадь = 5 см × 5 см = 25 см²
Таким образом, чтобы вычислить площадь квадрата, достаточно знать длину одной его стороны и возвести ее в квадрат.
Получение стороны квадрата
Для вычисления площади треугольника, полученного из квадрата, необходимо знать длину его стороны. Сторона квадрата может быть найдена по различным способам:
- Используя известные параметры треугольника: Если известны длина высоты треугольника и одной его стороны, то длина стороны квадрата равна удвоенной площади треугольника, деленной на длину высоты.
- Применяя теорему Пифагора: Если известна длина гипотенузы треугольника, то сторона квадрата равна квадратному корню из суммы квадратов катетов.
- Вычисляя длину стороны на основе угла наклона: Если известен угол наклона треугольника, то сторона квадрата равна произведению длины отрезка, соединяющего вершину треугольника и середину противоположной стороны, на тангенс угла наклона.
Какой из этих способов использовать - зависит от доступных данных и предпочтений пользователя. После получения длины стороны квадрата можно приступить к расчету его площади, используя формулу: S = a * a, где a - длина стороны квадрата.
Определение высоты треугольника

Для определения высоты треугольника можно воспользоваться различными методами:
| Метод | Описание |
|---|---|
| Метод через формулу площади | Если известны длины основания и высоты, можно воспользоваться формулой S = 1/2 * b * h, где S – площадь треугольника, b – длина основания, h – высота треугольника. |
| Метод через теорему Пифагора | Если известны длины сторон треугольника, можно воспользоваться теоремой Пифагора, чтобы найти высоту. Для прямоугольного треугольника высота будет являться одной из катетов, а для непрямоугольного треугольника высоту можно рассчитать используя формулу h = (2 * S) / a, где S – площадь треугольника, a – длина основания. |
| Метод через подобие треугольников | Если известны длины сторон и высоты другого подобного треугольника, можно воспользоваться подобием треугольников, чтобы найти высоту заданного треугольника. |
Определение высоты треугольника позволяет точнее рассчитать его площадь и является неотъемлемым шагом в геометрии.
Нахождение основания треугольника
Если известны длины двух сторон и значение угла между ними, для нахождения основания треугольника можно воспользоваться теоремой косинусов. Согласно этой теореме, квадрат длины основания треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула для нахождения основания треугольника с использованием теоремы косинусов выглядит следующим образом:
a^2 = b^2 + c^2 - 2bc*cosA
где a - длина основания треугольника, b и c - длины других двух сторон, A - значение угла между этими двумя сторонами.
Подставляя известные значения в данную формулу и решая ее, можно найти длину основания треугольника.
Вычисление площади треугольника

Площадь треугольника можно вычислить различными способами, в зависимости от того, какая информация о нем известна.
Если известны длины двух сторон треугольника и угол между ними, можно воспользоваться формулой для вычисления площади по формуле:
S = (a * b * sin(α)) / 2
Где a и b - длины сторон треугольника, α - угол между этими сторонами.
Если известны длины всех трех сторон треугольника, можно воспользоваться формулой Герона:
S = √(p * (p - a) * (p - b) * (p - c))
Где p - полупериметр треугольника, a, b и c - длины его сторон.
Если известны координаты вершин треугольника в декартовой системе координат, площадь можно вычислить с помощью формулы Гаусса:
S = |(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2)) / 2|
Где (x1, y1), (x2, y2) и (x3, y3) - координаты вершин треугольника.
Выбор метода вычисления площади треугольника зависит от доступной информации о нем.
Некоторые примеры решения задачи

Для нахождения площади треугольника, образованного диагоналями квадрата, можно использовать различные методы. Рассмотрим несколько из них:
1. Использование формулы Герона: Если известны длины всех сторон треугольника, то площадь можно найти с помощью формулы Герона: S = √(p(p-a)(p-b)(p-c)), где S - площадь треугольника, a, b, c - длины сторон, p - полупериметр (p = (a + b + c) / 2).
2. Использование высоты треугольника: Если известна длина стороны квадрата и длина высоты, опущенной на эту сторону, то площадь можно найти, умножив половину длины стороны на длину высоты: S = (a * h) / 2, где S - площадь треугольника, a - длина стороны квадрата, h - длина высоты.
3. Использование теоремы Пифагора: Если известна длина гипотенузы треугольника и длины двух катетов, то площадь можно найти с помощью формулы: S = (c * (b - a)) / 2, где S - площадь треугольника, c - длина гипотенузы, a, b - длины катетов.
Выбор метода зависит от доступных данных о треугольнике. Важно помнить, что для правильного решения задачи необходимо использовать правильные формулы и проверять соответствие входных данных требованиям выбранного метода.