Треугольник - одна из основных геометрических фигур, которая имеет три стороны и три угла. Одним из самых важных параметров треугольника является его площадь, которая определяет, сколько плоскости занимает данная фигура. Площадь треугольника может быть вычислена различными способами, в зависимости от известных данных.

Формула для вычисления площади треугольника зависит от того, какие данные у нас изначально имеются. Если известна длина основания треугольника (одной из его сторон) и высота, проведенная к этой стороне, то площадь может быть вычислена по формуле: S = (a * h) / 2, где S - площадь треугольника, a - длина основания, h - высота.

Если известны длины всех трех сторон треугольника, то площадь можно вычислить по формуле Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь треугольника, p - полупериметр треугольника (p = (a + b + c) / 2), a, b, c - длины сторон треугольника.

Существует также метод нахождения площади треугольника с помощью векторного произведения двух сторон треугольника. Этот метод основан на свойствах векторного произведения и более сложен для понимания и использования, но иногда может использоваться для нахождения площади треугольника в векторной форме.

Геометрия треугольника и основные понятия

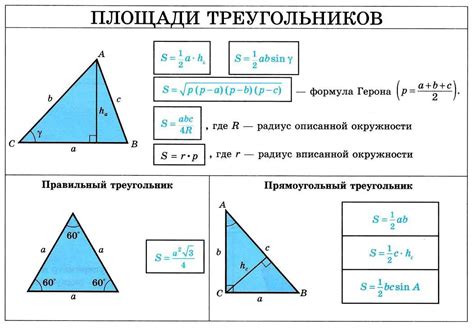
Длины сторон треугольника обозначаются как a, b и c. Углы треугольника обозначаются как A, B и C, где A соответствует стороне a и так далее. Сумма углов треугольника всегда равна 180 градусам.

Высота треугольника - это перпендикуляр, опущенный из одной из вершин на противоположную сторону (или его продолжение). Она обозначается как h и может быть вычислена с использованием различных методов, включая формулы, основанные на сторонах и углах треугольника.

Медианы треугольника - это отрезки, соединяющие каждую вершину треугольника с серединой противоположной стороны. Они обозначаются как m_a, m_b и m_c. Медианы делят каждую сторону треугольника пополам и пересекаются в общей точке, называемой центром медиан треугольника.

Знание этих основных понятий и связанных с ними формул позволяет более точно изучать геометрию треугольника и рассчитывать его площадь с помощью различных методов.

Формула Герона и ее применение

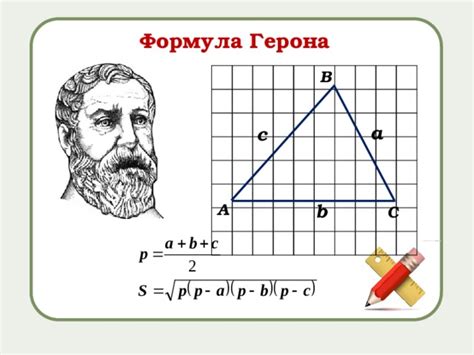
Для применения формулы Герона необходимо знать длины всех трех сторон треугольника. Обозначим эти длины как a, b и c. Тогда площадь S треугольника может быть вычислена по следующей формуле:

где p – полупериметр треугольника, который можно вычислить по формуле:

Формула Герона имеет ряд применений в геометрии. Она позволяет вычислить площадь треугольника, имея лишь длины его сторон. Это особенно полезно, если у нас нет возможности измерить высоту треугольника или применить другие способы расчета площади.

Кроме того, формула Герона может быть использована для проверки правильности измерений треугольника. Если полученное значение площади, вычисленное по формуле Герона, отличается от ожидаемого, то может быть ошибка в измерениях или постройке треугольника.

Вычисление площади треугольника через высоту и основание

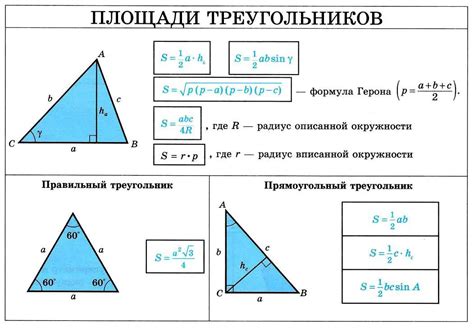
Высотой треугольника называется отрезок, проведенный из вершины треугольника до прямой, на которой лежит его основание и перпендикулярен ей. Основанием треугольника является произвольная сторона, на которую опирается высота.

Формула для вычисления площади треугольника через высоту и основание имеет вид:

S = (а * h) / 2,

где S - площадь треугольника, а - длина основания, h - высота.

Чтобы вычислить площадь треугольника по этой формуле, необходимо знать длину основания и высоту треугольника. Основание можно измерить непосредственно на самом треугольнике или получить его значение из других данных. Высоту можно вычислить с помощью геометрических методов или получить ее значение из условия задачи либо известных данных о треугольнике.

Основание и высоту треугольника можно обозначать разными буквами, в зависимости от условия задачи или используемых обозначений. Однако, важно при расчете использовать соответствующие значения и правильно подставлять их в формулу для вычисления площади треугольника.

Вычисление площади треугольника через высоту и основание - один из способов определить площадь этой геометрической фигуры и может быть использован в различных задачах и ситуациях, требующих расчета площади треугольника.