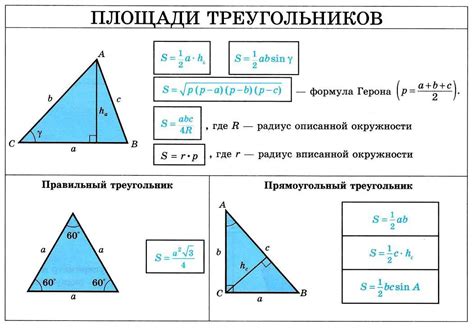
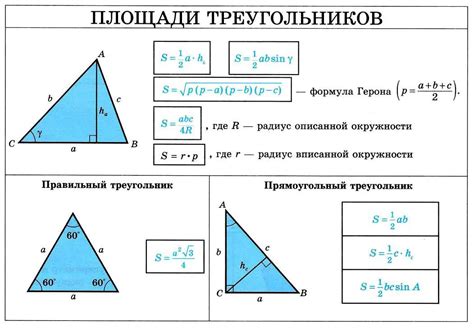
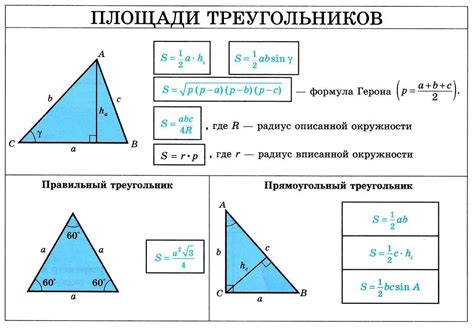
Расчет площади треугольника – это одна из базовых задач геометрии, которую важно знать для решения множества практических задач. Независимо от того, является ли треугольник прямоугольным, равносторонним или произвольным, существует универсальная формула, позволяющая найти его площадь.
Формула для расчета площади треугольника: S = 0.5 * a * h, где S – площадь треугольника, a – длина одной из сторон, а h – высота, опущенная на эту сторону. Если известны длины всех трех сторон треугольника, можно воспользоваться формулой Герона для расчета площади.
Примеры расчетов:
1. Допустим, сторона треугольника равна 6 см, а высота, опущенная на эту сторону, равна 4 см. Применяя формулу S = 0.5 * a * h, получаем S = 0.5 * 6 * 4 = 12 см². Таким образом, площадь треугольника равна 12 квадратным сантиметрам.
2. Если известны длины всех трех сторон треугольника, скажем, a = 8 см, b = 10 см и c = 12 см, можно воспользоваться формулой Герона: S = √(p * (p - a) * (p - b) * (p - c)), где p – полупериметр треугольника, вычисляемый как p = (a + b + c) / 2. Подставляя значения, получаем p = (8 + 10 + 12) / 2 = 15 см и S = √(15 * (15 - 8) * (15 - 10) * (15 - 12)) = √(15 * 7 * 5 * 3) ≈ 19.06 квадратных сантиметров.
Теперь, зная основные формулы и принципы расчета площади треугольника, вы сможете легко решать задачи геометрии и применять эти знания в практике.
Формула площади треугольника и способы ее нахождения
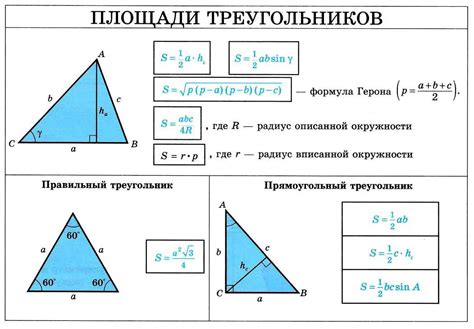
Наиболее распространенной формулой для вычисления площади треугольника является формула Герона. Данная формула основывается на полупериметре треугольника (сумма длин его сторон, деленная на 2) и длинах его сторон. Формула Герона имеет следующий вид:
| S = √(p * (p - a) * (p - b) * (p - c)) |
где S - площадь треугольника, p - полупериметр треугольника (p = (a + b + c) / 2), a, b, c - длины сторон треугольника.
Для примера, рассмотрим треугольник со сторонами a = 6, b = 8 и c = 10. В этом случае, полупериметр будет равен p = (6 + 8 + 10) / 2 = 12. Подставляя значения в формулу, получаем:
| S = √(12 * (12 - 6) * (12 - 8) * (12 - 10)) |
| S = √(12 * 6 * 4 * 2) |
| S = √(576) |
| S ≈ 24 |
Таким образом, площадь треугольника со сторонами 6, 8 и 10 примерно равна 24 единицам площади.
Кроме формулы Герона, существует также другой способ нахождения площади треугольника - с использованием высоты. Высота треугольника - это перпендикуляр, опущенный из вершины треугольника на противоположную сторону. Площадь треугольника можно найти, умножив длину стороны на соответствующую высоту и разделив полученное значение на 2. Формула для расчета площади треугольника с использованием высоты выглядит следующим образом:
| S = (a * h) / 2 |
где S - площадь треугольника, a - длина стороны треугольника, h - высота, опущенная на эту сторону.
Оба этих способа являются эффективными и позволяют подсчитать площадь треугольника в зависимости от данных, которые имеются. Выбор конкретного способа зависит от известных параметров треугольника и предпочтений самого исследователя.
Расчет площади треугольника по основанию и высоте
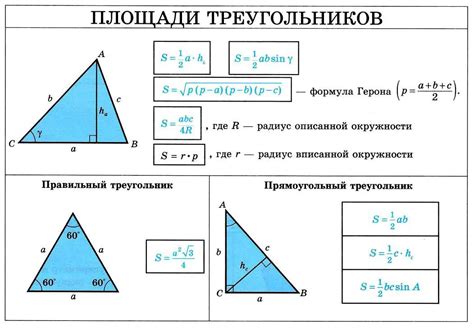
Площадь треугольника можно найти с использованием формулы, которая основывается на длине его основания и высоте. Для расчета площади треугольника по основанию и высоте используется следующая формула:
S = (b * h) / 2,
где S - площадь треугольника, b - длина основания треугольника, h - высота треугольника, опущенная на основание.
Чтобы найти площадь треугольника, необходимо знать значения основания и высоты. Значения этих параметров можно измерить с помощью линейки или получить из задачи или геометрической фигуры.
Давайте рассмотрим пример расчета площади треугольника по основанию и высоте:
Пусть основание треугольника равно 5 см, а высота равна 3 см.
Применяя формулу, рассчитываем площадь треугольника:
S = (5 * 3) / 2 = 7.5 см².
Таким образом, площадь треугольника равна 7.5 см².
Нахождение площади треугольника по трем сторонам
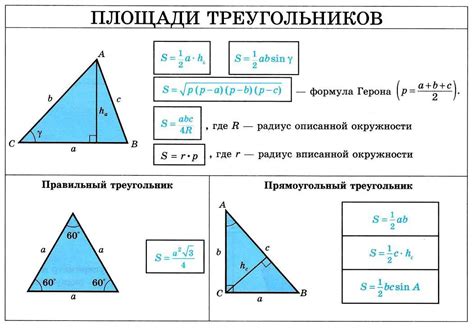
Для нахождения площади треугольника, когда известны длины его трех сторон, можно воспользоваться формулой Герона. Формула Герона основана на полупериметре треугольника, который вычисляется как сумма длин всех его сторон, разделенная на 2.
По формуле Герона, площадь треугольника находится по следующей формуле:
S = √(p(p-a)(p-b)(p-c)),
где S - площадь, а, b и c - длины сторон треугольника, p - полупериметр.
Используя данную формулу, можно вычислить площадь треугольника по значениям его сторон. Нужно только знать длины всех трех сторон треугольника.
Примеры вычисления площади треугольника:
- Строим треугольник со сторонами длиной 5, 6 и 7.
- Вычисляем полупериметр треугольника: p = (5 + 6 + 7) / 2 = 9.
- Применяем формулу Герона: S = √(9(9-5)(9-6)(9-7)) = √(9*4*3*2) = √216 = 14.6969.
- Таким образом, площадь треугольника равна 14.6969 квадратных единиц.
Пользуясь данной формулой, вы сможете легко находить площадь треугольника, зная значения всех его сторон. Это может пригодиться в различных задачах, требующих вычислений площадей треугольников.
Расчет площади треугольника по двум сторонам и углу между ними
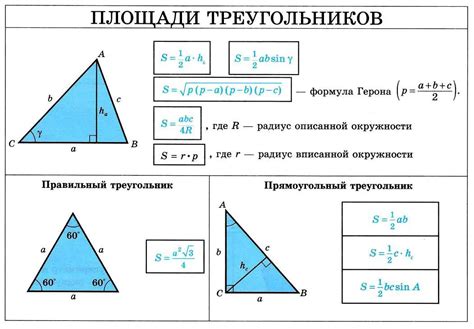
Площадь треугольника можно вычислить разными способами в зависимости от доступных данных. Если известны две стороны треугольника и угол между ними, то можно воспользоваться формулой Герона, модифицированной для данного случая.
Формула для расчета площади треугольника S по двум сторонам a и b и углу α между ними:
- Вычислите длину третьей стороны треугольника c по формуле c = √(a² + b² - 2ab·cosα)
- Вычислите полупериметр треугольника p по формуле p = (a + b + c) / 2
- Вычислите площадь треугольника S по формуле S = √(p(p - a)(p - b)(p - c))
Например, у нас есть треугольник со сторонами a = 5, b = 7 и углом α = 45°. Вычислим площадь этого треугольника:
- Длина третьей стороны c = √(5² + 7² - 2·5·7·cos45°) = √(25 + 49 - 70·0.7071) ≈ √(74 - 49.497) ≈ √24.543 ≈ 4.954
- Полупериметр треугольника p = (5 + 7 + 4.954) / 2 ≈ 8.954
- Площадь треугольника S = √(8.954(8.954 - 5)(8.954 - 7)(8.954 - 4.954)) ≈ √(8.954·3.954·1.954·4.954) ≈ √279.7 ≈ 16.72
Таким образом, площадь треугольника с заданными сторонами и углом между ними составляет примерно 16.72 квадратных единиц.
Примеры расчета площади треугольника с конкретными значениями
Чтобы наглядно проиллюстрировать процесс расчета площади треугольника, рассмотрим несколько конкретных примеров:
Пример 1: Рассчитаем площадь треугольника, если известны его основание и высота. Пусть основание треугольника равно 6 см, а высота - 4 см.
Площадь треугольника равна: (6 см * 4 см) / 2 = 12 кв.см
Пример 2: Рассчитаем площадь треугольника по трем его сторонам, используя формулу Герона. Пусть стороны треугольника равны 5 см, 7 см и 8 см.
Сначала рассчитаем полупериметр треугольника: полупериметр = (5 см + 7 см + 8 см) / 2 = 20 / 2 = 10 см
Затем применим формулу Герона: площадь треугольника = квадратный корень из (10 см * (10 см - 5 см) * (10 см - 7 см) * (10 см - 8 см)) = квадратный корень из (10 см * 5 см * 3 см * 2 см) ≈ 10 кв.см
Пример 3: Рассчитаем площадь треугольника по координатам вершин на плоскости. Пусть координаты вершин треугольника A(1, 1), B(4, 5) и C(7, 2).
Сначала найдем длины сторон треугольника, используя формулу расстояния между точками: AB = √((x2 - x1)² + (y2 - y1)²), где (x1, y1) и (x2, y2) - координаты концов стороны.
AB = √((4 - 1)² + (5 - 1)²) = √(9 + 16) = √25 = 5
BC = √((7 - 4)² + (2 - 5)²) = √(9 + 9) = √18 ≈ 4.24
AC = √((7 - 1)² + (2 - 1)²) = √(36 + 1) = √37 ≈ 6.08
Затем рассчитаем полупериметр треугольника: полупериметр = (5 + 4.24 + 6.08) / 2 ≈ 7.66
Наконец, применим формулу Герона: площадь треугольника = квадратный корень из (7.66 * (7.66 - 5) * (7.66 - 4.24) * (7.66 - 6.08)) ≈ 11.25
Как использовать площадь треугольника в реальной жизни
Например, в строительстве площадь треугольника может быть использована для расчета площади крыши, площади фасадов здания, площади пола, площади окон и дверей. Зная площадь треугольника, строители могут более точно распределить ресурсы и материалы, а также определить стоимость строительных работ.
Площадь треугольника также применяется в геометрии и физике. В геометрии площадь треугольника может быть использована для нахождения других параметров треугольника, таких как высота, медиана, периметр и радиус вписанной окружности. В физике площадь треугольника может быть использована для расчета площади поверхности тела или расчета работы при перемещении тела.
Кроме того, знание площади треугольника может быть полезно в повседневной жизни для решения различных задач. Например, при выборе ковра или площади комнаты для укладки напольного покрытия, знание площади треугольника поможет определить необходимое количество материала. Также, площадь треугольника может быть использована при расчете вписывающегося прямоугольника для выполнения складки квадратного материала, такого как бумага или ткань.
Все это подтверждает важность знания площади треугольника и его широкое применение в реальной жизни. Расчет площади треугольника - это базовая математическая операция, которая может быть использована во множестве различных сфер нашей жизни.
Более сложные способы нахождения площади треугольника
Помимо базовой формулы для нахождения площади треугольников, которая основана на длинах его сторон и позволяет рассчитывать площадь для треугольников любой формы, существуют и другие, более сложные методы для определения площади треугольника. Вот некоторые из них:
- Формула Герона: Этот метод основан на полупериметре треугольника и длинах его сторон. Формула Герона позволяет рассчитать площадь треугольника, не зная его высоту. Она выглядит следующим образом:
S = √(p(p-a)(p-b)(p-c)),
где S - площадь треугольника, p - полупериметр треугольника, a, b, c - длины его сторон.
- Два вектора: Если известны координаты вершин треугольника, его площадь можно найти, используя два вектора, проходящих через эти вершины. Для этого вычисляются координаты этих векторов, затем их векторное произведение, и наконец, находится половина модуля этого векторного произведения.
S = 0.5 * |(x1 - x3)(y2 - y3) - (x2 - x3)(y1 - y3)|,
где S - площадь треугольника, (x1, y1), (x2, y2) и (x3, y3) - координаты его вершин.
- Формула Брахмагупты: Этот метод основан на формуле, предложенной индийским математиком Брахмагуптой, и позволяет находить площадь любого четырехугольника, включая треугольники. Формула Брахмагупты выглядит следующим образом:
S = √((s-a)(s-b)(s-c)(s-d)),
где S - площадь треугольника, s - полупериметр треугольника, a, b, c, d - длины его сторон.
Использование этих более сложных методов может быть полезно в определенных ситуациях, особенно если известны только длины сторон треугольника или его координаты. Однако, при обычных задачах нахождения площади треугольника, базовая формула обычно является достаточной и более простой в использовании.