Площадь треугольника является одним из наиболее важных параметров этой геометрической фигуры. Расчет площади треугольника может понадобиться в различных ситуациях, например, при решении задач по физике, архитектуре или геодезии. В этой статье рассмотрим, как найти площадь треугольника по длинам его сторон.
Существует несколько способов вычисления площади треугольника, и одним из самых простых и удобных является использование формулы Герона. Формула Герона позволяет вычислить площадь треугольника, зная длины всех его сторон. Эта формула основана на полупериметре треугольника, который вычисляется по формуле: полупериметр = (a + b + c) / 2, где a, b и c - длины сторон треугольника. Площадь треугольника по формуле Герона вычисляется по следующей формуле:
S = √(p × (p - a) × (p - b) × (p - c))
где S - площадь треугольника, p - полупериметр, а a, b и c - длины сторон треугольника.
Вычисление площади треугольника по данной формуле является достаточно простым, и может быть выполнено с помощью калькулятора или программы для работы с числами с плавающей запятой. Важно учесть, что длины сторон треугольника должны быть положительными числами и удовлетворять условию треугольника - сумма длин двух сторон должна быть больше длины третьей стороны.
Как найти площадь треугольника?
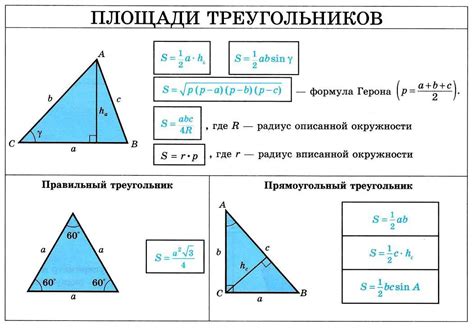
Существует несколько способов вычисления площади треугольника, однако наиболее распространенным и удобным является способ по формуле Герона.
Для применения формулы Герона необходимо знать длины всех трех сторон треугольника, обозначим их как a, b и c.
Формула Герона для вычисления площади треугольника имеет следующий вид:
S = √(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, p - полупериметр треугольника (p = (a + b + c) / 2).
Используя данную формулу, вы можете легко и быстро вычислить площадь треугольника по заданным значениям сторон.
Формула расчета площади треугольника
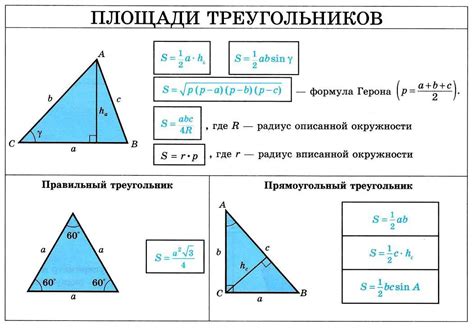
Существует несколько способов расчета площади треугольника, включая формулы, основанные на его высоте, радиусе вписанной окружности и длинах сторон треугольника.
Формула Герона – один из наиболее распространенных способов расчета площади треугольника, основанный на длинах его сторон. Формула выглядит следующим образом:
- Пусть a, b и c – длины сторон треугольника;
- Полупериметр треугольника p = (a + b + c) / 2;
- Площадь треугольника S = √(p * (p-a) * (p-b) * (p-c)), где √ обозначает операцию извлечения квадратного корня.
Формула Герона основана на теореме Герона, которая гласит, что площадь треугольника можно вычислить, зная длины его сторон и полупериметр.
Эта формула предоставляет простой и эффективный способ вычисления площади треугольника, не требующий измерения углов или построения высоты треугольника.
Благодаря формуле Герона, расчет площади треугольника по его сторонам становится доступным и позволяет быстро и точно определить площадь треугольника в различных задачах и ситуациях.
Понятие площади треугольника

Площадь треугольника, как и любой другой плоской фигуры, выражается в квадратных единицах – квадратных метрах, квадратных сантиметрах и т.д. Для нахождения площади треугольника существуют различные формулы, одна из которых основана на длинах сторон треугольника.
Формула для расчета площади треугольника по длинам сторон (формула Герона) имеет вид:
| Формула: | S = √(p(p-a)(p-b)(p-c)) |
|---|
Где:
- S – площадь треугольника;
- a, b, c – длины сторон треугольника;
- p – полупериметр треугольника, равный половине суммы длин всех сторон: p = (a + b + c) / 2.
То есть, чтобы найти площадь треугольника по длинам его сторон, нужно вычислить полупериметр по формуле, а затем использовать его в формуле Герона. Результатом будет площадь треугольника в соответствующих единицах измерения.
Зная площадь треугольника, можно решать различные задачи, связанные с этой геометрической фигурой, например, находить площадь составных фигур, определять высоту треугольника, вычислять углы треугольника и многое другое.
Как найти длины сторон треугольника?

Для вычисления площади треугольника необходимо знать длины его сторон. Существует несколько способов найти эти значения, в зависимости от доступной информации.
Если известны координаты вершин треугольника, можно использовать формулу расстояния между двумя точками в двумерном пространстве. Для каждой пары вершин можно посчитать расстояние и получить значения сторон треугольника.
Если известны углы треугольника и одна сторона, можно использовать тригонометрические функции для нахождения длин остальных сторон. Например, для нахождения сторон треугольника, когда известны угол α и сторона а, можно воспользоваться формулой a/sinα = b/sinβ = c/sinγ, где α, β и γ - углы треугольника, a, b и c - длины сторон.
Если известны площадь треугольника и одна из его сторон, можно воспользоваться другой формулой. Площадь треугольника равна половине произведения длин двух его сторон и синуса между ними. Используя эту формулу и известную площадь, можно выразить неизвестную величину и найти длину другой стороны.
Важно помнить, что для нахождения длин сторон треугольника часто необходимо знать как можно больше информации о фигуре. Это могут быть координаты вершин, значения углов, площадь и т.д. Чем больше информации доступно, тем точнее можно определить длины сторон треугольника.
Применение формулы Герона
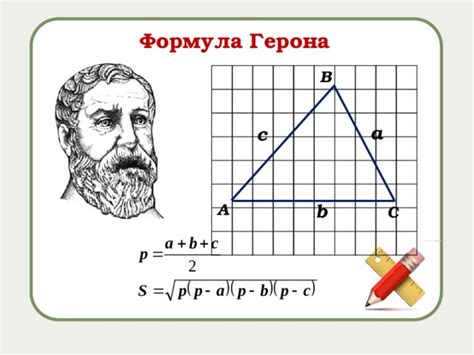
Применение формулы Герона состоит из нескольких шагов:
- Измерьте длины всех трех сторон треугольника. Назовем их a, b и c.
- Вычислите полупериметр треугольника, используя формулу: p = (a + b + c) / 2.
- Вычислите площадь треугольника с помощью формулы Герона: S = √(p * (p - a) * (p - b) * (p - c)), где p - полупериметр, a, b и c - длины сторон треугольника.
Применение формулы Герона может быть особенно полезным, когда известны только длины сторон треугольника, а другие данные, такие как высота или углы, неизвестны.
Этот метод находит широкое применение в геометрии, архитектуре, инженерии и других областях, где требуется вычисление площади треугольников по известным данным. Формула Герона является простым и эффективным инструментом для решения подобных задач.
Примеры расчета площади треугольника
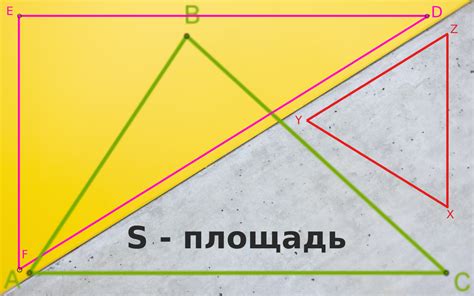
Расчёт площади треугольника может быть выполнен с использованием формулы Герона, которая основывается на длинах его сторон.
Пусть дан треугольник ABC, его стороны обозначены как AB, BC и CA, соответственно.
Пример 1:
Известно, что длина стороны AB равна 5, длина стороны BC равна 4 и длина стороны CA равна 3.
Используя формулу Герона:
полупериметр треугольника p = (AB + BC + CA) / 2 = (5 + 4 + 3) / 2 = 12 / 2 = 6
площадь треугольника S = √(p × (p - AB) × (p - BC) × (p - CA)) = √(6 × (6 - 5) × (6 - 4) × (6 - 3)) = √(6 × 1 × 2 × 3) = √(36) = 6
Площадь треугольника ABC равна 6.
Пример 2:
Допустим, у треугольника ABC длина стороны AB равна 8, длина стороны BC равна 6 и длина стороны CA равна 10.
Используя формулу Герона:
полупериметр треугольника p = (AB + BC + CA) / 2 = (8 + 6 + 10) / 2 = 24 / 2 = 12
площадь треугольника S = √(p × (p - AB) × (p - BC) × (p - CA)) = √(12 × (12 - 8) × (12 - 6) × (12 - 10)) = √(12 × 4 × 6 × 2) = √(576) = 24
Площадь треугольника ABC равна 24.
Таким образом, используя формулу Герона, мы можем легко вычислить площадь треугольника, зная длины его сторон.
В данной статье мы изучили формулу расчета площади треугольника по длинам его сторон.
Мы узнали, что для нахождения площади треугольника необходимо знать длины всех его сторон, а также использовать формулу Герона. Эта формула позволяет нам вычислить полупериметр треугольника и далее найти площадь, используя теорему Герона.
Также мы обратили внимание, что при использовании данной формулы необходимо быть внимательными к величинам длин сторон треугольника, так как они должны обладать определенными свойствами:
- Длина каждой стороны должна быть больше нуля.
- Сумма длин двух сторон должна быть больше длины третьей стороны.
Теперь, зная формулу расчета площади треугольника по длинам его сторон, мы можем легко и быстро находить площадь треугольника, даже если известны только длины его сторон.