Насколько вы хорошо помните геометрию из школьных лет? Может быть, вы забыли многие формулы, но, к счастью, на практике не все задачи требуют воспоминаний изученного материала. Найти площадь треугольника - одна из самых частых задач, которые периодически возникают в различных сферах нашей жизни. И хотя мы можем вспомнить формулу, чтобы сделать это легко и быстро, давайте вспомним, как можно это сделать без необходимости в запоминании формул.
Переменный треугольник может быть вызовом для тех, кто не знает формулы площади треугольника. Однако все треугольники имеют одну общую формулу для расчета площади, которая может быть легко запомнена. Эта формула называется формулой Герона. Герон, это знаменитый античный греческий математик, который, среди многого другого, создал одну из величайших формул в истории математики - формулу Герона.
Что делает формулу Герона легкой в запоминании? Это то, что она основана на длинах сторон треугольника. То есть, вы не будете искать или запоминать дополнительные параметры, такие как радиусы окружности или углы. Вам просто нужно знать длины сторон треугольника. Формула Герона избавляет вас от необходимости помнить сколько-то кнопчики и позволяет вам сосредоточиться на самой сути задачи - нахождении площади треугольника. Итак, давайте воспользуемся формулой Герона и узнаем, как легко и быстро можно найти площадь треугольника.
Что такое треугольник и как найти его площадь
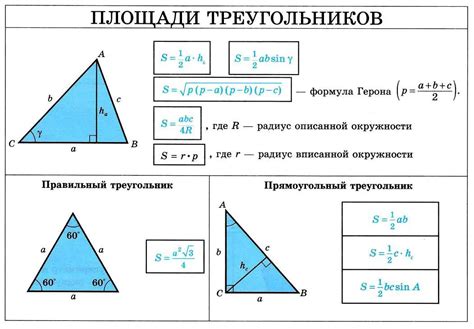
Для нахождения площади треугольника необходимо знать длины его сторон или длину одной стороны и высоту, опущенную на эту сторону. Существует несколько способов вычисления площади треугольника, в зависимости от доступных данных.
Одним из способов вычисления площади треугольника является использование формулы Герона. Она основана на полупериметре треугольника - сумме длин его сторон, деленной на 2. Площадь треугольника по формуле Герона выглядит так:
S = √(p * (p - a) * (p - b) * (p - c))
где S - площадь треугольника, p - полупериметр треугольника, a, b, c - длины его сторон.
Другим способом нахождения площади треугольника является использование формулы, которая использует длину одной стороны и высоту, опущенную на эту сторону. Площадь треугольника по этой формуле выражается следующим образом:
S = (a * h) / 2
где S - площадь треугольника, a - длина стороны треугольника, h - высота, опущенная на эту сторону.
Независимо от выбранного метода, правильный расчет площади треугольника позволяет нам определить, какая площадь занимает эта фигура в плоскости.
Треугольник: определение и основные составляющие

Основные составляющие треугольника:
- Стороны - это линейные отрезки, которые соединяют вершины треугольника. Каждая сторона имеет свою длину, которая может быть измерена.
- Вершины - это точки пересечения сторон треугольника. У треугольника всегда три вершины.
- Углы - это области пространства между сторонами треугольника. У треугольника всегда три угла, которые суммируются в 180 градусов.
Треугольники могут быть различных типов в зависимости от длин сторон и величины углов. Некоторые из наиболее распространенных типов треугольников включают прямоугольный треугольник, равнобедренный треугольник и равносторонний треугольник.
Формула для вычисления площади треугольника
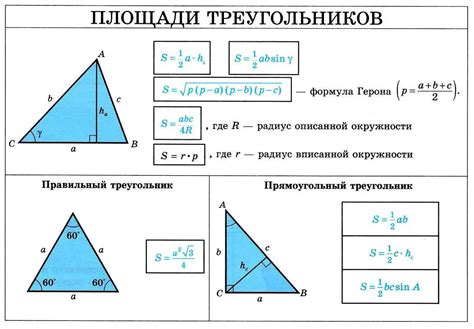
Площадь треугольника может быть вычислена с использованием простой формулы, которая зависит от длины основания треугольника и его высоты.
Формула для вычисления площади треугольника выглядит следующим образом:
| Площадь треугольника (S) | = | (Основание (b) * Высота (h)) / 2 |
В этой формуле, основание (b) - это длина одной из сторон треугольника, а высота (h) - это расстояние от основания треугольника до противоположного угла.
Для примера, если основание треугольника равно 6 единицам, а высота равна 4 единицам, то площадь треугольника можно рассчитать следующим образом:
| Площадь треугольника (S) | = | (6 * 4) / 2 | = | 12 единицы квадратные |
Таким образом, формула для вычисления площади треугольника является простой и эффективной, позволяя быстро и легко найти площадь треугольника при известном основании и высоте.
Как найти основание и высоту треугольника
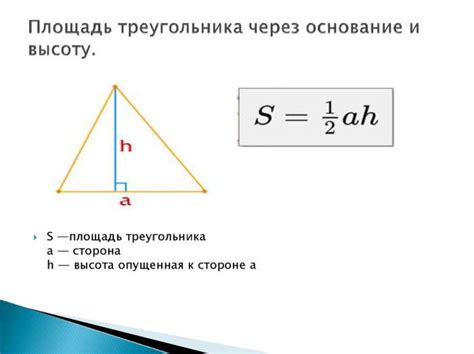
Если у вас есть треугольник и вы знаете длину одной его стороны (основание) и высоту, то вы можете легко вычислить его площадь по формуле.
Чтобы найти основание треугольника, вам понадобится измерительная лента или линейка. Просто измерьте длину одной из сторон треугольника - это и будет основание.
Для определения высоты треугольника вам потребуется знать его основание и угол между этим основанием и противоположной стороной. Если у вас отсутствует угол, но известна длина стороны, величину угла можно найти, используя тригонометрические функции синуса или косинуса.
Используя полученные значения основания и высоты, вы можете применить формулу для нахождения площади треугольника. Площадь треугольника равна половине произведения его основания на высоту.
Теперь, зная основание и высоту треугольника, вы сможете легко и быстро вычислить его площадь и использовать полученный результат в различных математических и геометрических задачах.
| Известные значения: | Формула для вычисления площади: |
|---|---|
| Основание треугольника (a) | Площадь = 0,5 * a * h |
| Высота треугольника (h) |
Примеры вычисления площади треугольника
Давайте рассмотрим несколько примеров вычисления площади треугольника по формуле. В формуле площади треугольника используется длина основания и высота, которую можно определить по разным способам.
Пример 1:
Пусть треугольник имеет основание длиной 6 см и высоту 4 см. Для вычисления площади треугольника по формуле, умножим длину основания на высоту и разделим полученное значение на 2:
Площадь = (6 см * 4 см) / 2 = 12 см2
Пример 2:
Пусть треугольник имеет основание длиной 10 см и высоту 8 см. Для вычисления площади треугольника по формуле сначала умножим длину основания на высоту, а затем разделим полученное значение на 2:
Площадь = (10 см * 8 см) / 2 = 40 см2
Пример 3:
Пусть треугольник имеет основание длиной 12 см и высоту 6 см. Для вычисления площади треугольника по формуле, умножим длину основания на высоту и разделим полученное значение на 2:
Площадь = (12 см * 6 см) / 2 = 36 см2
Таким образом, мы видим, что вычисление площади треугольника по формуле является простым и эффективным способом определения площади данной геометрической фигуры.
Советы для упрощения вычислений площади треугольника
Вычисление площади треугольника может быть достаточно сложным процессом, но с правильными советами можно значительно упростить эту задачу. Вот несколько советов, которые помогут вам справиться с этой математической задачей быстро и легко:
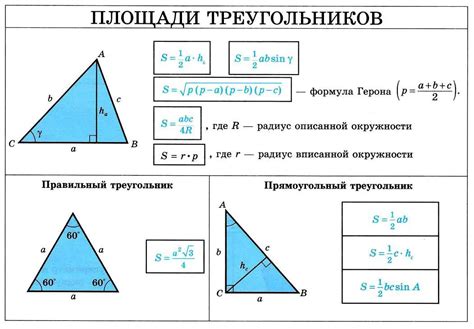
1. Используйте формулу Герона: Площадь треугольника можно вычислить, используя формулу Герона, которая основана на сторонах треугольника и его полупериметре. Используя эту формулу, вы сможете избежать сложных вычислений и получить точный результат.
2. Проверьте правильность измерений: Перед тем, как вычислять площадь треугольника, убедитесь, что ваши измерения сторон треугольника точны. Даже небольшие ошибки в измерениях могут привести к неточному результату.
3. Используйте полуреку: Если у вас есть треугольник, у которого известны длины двух сторон и их включающего угла, вы можете использовать полуреку для вычисления площади треугольника. Полурека - это математическая формула для вычисления площади треугольника, использующая урезанный синус вместо обычного.
4. Используйте тригонометрию: Если у вас есть треугольник, у которого известна одна сторона и два угла, то вы можете использовать тригонометрические функции (синус и косинус) для вычисления площади треугольника. Тригонометрия позволяет связать стороны и углы треугольника и использовать их для вычисления площади.
Следуя этим советам, вы сможете упростить процесс вычисления площади треугольника и получить точный результат. И помните, практика делает мастера - чем больше треугольников вы будете измерять и вычислять их площадь, тем более опытными вы станете в этой области.
Одним из простых применений формулы площади треугольника является вычисление площади участка земли. Например, если вы хотите забором огород или участок на даче, вам может понадобиться вычислить его площадь, чтобы правильно распределить материалы и ресурсы. Формула площади треугольника поможет вам быстро и точно определить этот показатель.
Еще одним примером применения формулы площади треугольника может быть расчет площади крыши или фасада здания. Архитекторы, инженеры и строители используют эту формулу для того, чтобы определить, сколько материала им понадобится для покрытия поверхности.
Формула площади треугольника также может быть полезной при решении задач, связанных с планированием и дизайном интерьера. Например, вы можете использовать эту формулу для определения площади ковра или обоев, которые вам понадобятся для отделки комнаты.
Кроме того, понимание формулы площади треугольника может помочь в решении разных задач в области науки и технологий. Например, инженеры, занимающиеся конструированием и проектированием структур, часто используют эту формулу для определения различных геометрических показателей.
В целом, знание формулы площади треугольника является полезным навыком и может быть полезным во многих сферах жизни. Будь то решение повседневных задач или взаимодействие со сложными техническими вопросами, эта формула может помочь нам более точно и эффективно оперировать понятием площади треугольника.