Площадь треугольника - одна из основных характеристик этой геометрической фигуры. Для ее нахождения существуют различные способы, в зависимости от известных данных. В данной статье мы рассмотрим, как найти площадь треугольника, если известны длины всех трех его сторон, и поделим эту информацию на формулу, доступную для изучения в 4 классе.
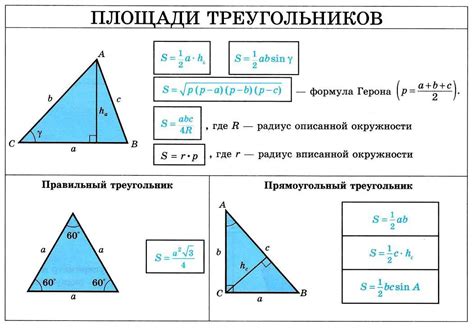
Формула для нахождения площади треугольника по 3 сторонам известна как формула Герона. Она была открыта уже в древней Греции математиком Героном Александрийским и до сих пор является одной из самых популярных и простых в использовании формул для вычисления площади треугольника.
Для применения формулы Герона нам необходимо знать длины всех трех сторон треугольника. Обозначим эти стороны как a, b и c. Площадь треугольника по формуле Герона можно вычислить по следующей формуле:
S = √(p * (p - a) * (p - b) * (p - c))
где p - полупериметр треугольника, который можно найти по формуле: p = (a + b + c) / 2.
Теперь, когда мы знаем формулу и условия для ее использования, мы можем приступить к расчету площади треугольника по 3 сторонам. Следует отметить, что данная формула подходит для треугольников любого типа и формы, включая разносторонние, равнобедренные и равносторонние треугольники.
Как найти площадь треугольника?
Для нахождения площади треугольника по трем сторонам можно воспользоваться формулой Герона. Для этого нужно выполнить несколько шагов.
1. Измерьте длину каждой стороны треугольника.
2. Сложите длины всех сторон и разделите полученную сумму на 2. Результат запишите в переменную "p".
3. Используя формулу Герона: S = √(p * (p - a) * (p - b) * (p - c)), где a, b и c - длины сторон, найдите площадь треугольника. Запишите результат в переменную "S".
4. Получите ответ: площадь треугольника равна "S".
Теперь вы знаете, как найти площадь треугольника по трем сторонам, используя формулу Герона. Помните, что все длины сторон должны быть положительными числами, иначе решение будет некорректным.
Формула для 4 класса

Для нахождения площади треугольника по заданным сторонам можно воспользоваться формулой Герона. Эта формула основывается на полупериметре треугольника и его сторонах.
Первым шагом необходимо найти полупериметр треугольника, сложив все его стороны и разделив полученную сумму на 2. Полупериметр будет обозначен как p.
Затем, используя полученное значение полупериметра, можно вычислить площадь треугольника по формуле Герона:
| Формула Герона: | S = √(p * (p - a) * (p - b) * (p - c)) |
Где:
- S - площадь треугольника
- p - полупериметр треугольника
- a, b, c - длины сторон треугольника
После подстановки значений в формулу можно произвести необходимые вычисления и найти площадь треугольника. Например, если даны стороны треугольника a = 5, b = 7 и c = 9, то:
Сначала находим полупериметр:
| p = (5 + 7 + 9) / 2 = 21 / 2 = 10.5 |
Затем используем формулу Герона:
| S = √(10.5 * (10.5 - 5) * (10.5 - 7) * (10.5 - 9)) |
После проведения вычислений получаем:
| S = √(10.5 * 5.5 * 3.5 * 1.5) = √(518.8125) ≈ 22.8 |
Площадь треугольника составляет примерно 22.8 квадратных единиц.
Используя эту формулу, ученики 4 класса могут с легкостью находить площадь треугольника по заданным сторонам. Это основа для дальнейшего изучения геометрии и построения различных фигур.
Использование 3 сторон

Для расчета площади треугольника по 3 сторонам можно воспользоваться формулой Герона. Формула Герона основана на полупериметре треугольника (сумма всех сторон, деленная на 2), и определяет площадь треугольника через длины его сторон.
Формула Герона выглядит следующим образом:
| S = | √(p * (p - a) * (p - b) * (p - c)) |
где:
- S - площадь треугольника
- p - полупериметр треугольника
- a, b, c - длины сторон треугольника
Для использования данной формулы необходимо знать длины всех трех сторон треугольника. Подставьте значения сторон в формулу и рассчитайте площадь треугольника с помощью калькулятора или вручную.