Треугольники - одна из основных геометрических фигур, которые мы изучаем в школе. Известно, что площадь треугольника можно вычислить с использованием различных формул, в зависимости от известных параметров. Однако, если известен только периметр и одна сторона треугольника, вычисление площади может показаться сложной задачей.
Однако, существует способ найти площадь треугольника с периметром и одной известной стороной, используя формулу Герона и свойства треугольников. Формула Герона позволяет вычислить площадь треугольника, зная его периметр и длины сторон.
По формуле Герона, площадь треугольника (S) можно вычислить по следующей формуле:
S = sqrt(p * (p - a) * (p - b) * (p - c)),
где p - полупериметр треугольника (p = (a + b + c) / 2), а a, b, c - длины сторон треугольника.
Используя эту формулу и известные значения периметра и одной стороны, мы можем вычислить площадь треугольника. Этот метод позволяет найти площадь треугольника, даже если не известны длины других сторон.
Что такое площадь треугольника
Площадь треугольника можно вычислить разными способами, в зависимости от известных данных. Один из самых простых способов - использовать длины сторон треугольника. Если известны длины всех трех сторон, можно использовать формулу Герона для вычисления площади.
Однако, если известен только периметр треугольника и одна его сторона, можно использовать формулу для вычисления площади путем нахождения высоты. Высоту можно выразить через радиусы вписанной и описанной окружностей и угол между этой стороной и смежными сторонами. После нахождения высоты используется формула для вычисления площади треугольника как произведение половины основания на высоту.
Знание площади треугольника позволяет сравнивать, классифицировать и анализировать треугольники, а также использовать их в решении задач различной прикладной математики и физики.
Формула для нахождения площади треугольника
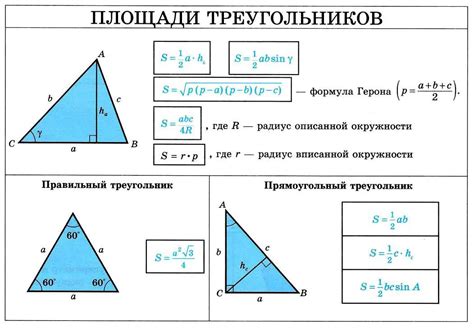
Площадь треугольника можно вычислить, зная длины его сторон и периметр. Данную задачу можно решить с помощью формулы герона или формулы с радиусом вписанной окружности.
Формула герона:
Пусть a, b и c – длины сторон треугольника, а p – его полупериметр (полусумма сторон), тогда площадь S может быть вычислена по формуле:
S = √(p*(p-a)*(p-b)*(p-c))
Формула с радиусом вписанной окружности:
Пусть r – радиус окружности, вписанной в треугольник, тогда площадь S может быть вычислена по формуле:
S = (a*b*c)/(4*r)
Выбор формулы зависит от доступных данных и предпочтений в решении задачи.
Как использовать периметр для расчета площади
1. Воспользуйтесь формулой Герона. Если известны длины всех сторон треугольника, можно использовать формулу Герона для расчета его площади:
полупериметр, s = (a + b + c) / 2
площадь треугольника, S = sqrt(s * (s - a) * (s - b) * (s - c))
Где a, b и c - длины сторон треугольника.
2. Рассчитайте высоту треугольника. Если известны длины одной стороны треугольника и высоты, опущенной на эту сторону, можно использовать формулу:
площадь треугольника, S = (a * h) / 2
Где a - длина стороны треугольника, h - высота, опущенная на эту сторону.
3. Используйте формулу площади прямоугольного треугольника. Если треугольник прямоугольный и известны длина гипотенузы и одной из катетов, можно использовать формулу:
площадь треугольника, S = (c * p) / 2
Где c - длина гипотенузы, p - длина катета.
Учитывайте, что для точного расчета площади треугольника необходимо знать длины всех его сторон или высоту, опущенную на одну из сторон. Если известна только одна сторона треугольника, периметр позволяет получить некоторую информацию о треугольнике, но необходимо дополнительно знать еще одну величину для точного расчета площади.
Примеры расчета площади треугольника
Рассмотрим несколько примеров расчета площади треугольника с заданным периметром и одной известной стороной.
Задан периметр треугольника равный 12 см, а также известна одна из его сторон, длина которой равна 4 см.
Для решения данной задачи можно использовать формулу для вычисления радиуса вписанной окружности:
Радиус вписанной окружности равен половине произведения стороны треугольника на площадь, разделенной на полупериметр:
Радиус = (длина стороны * площадь) / (полупериметр)
Для данного примера:
Радиус = (4 * площадь) / (12 / 2)
Подставив известные значения и решив полученное уравнение, найдем площадь треугольника.
Предположим, что периметр треугольника равен 18 см, а одна из его сторон имеет длину 6 см.
Для нахождения площади треугольника в этом случае можно воспользоваться формулой для радиуса описанной окружности:
Радиус описанной окружности равен произведению стороны треугольника на площадь, деленной на полупериметр:
Радиус = (длина стороны * площадь) / (полупериметр)
Для данного примера:
Радиус = (6 * площадь) / (18 / 2)
Подставив известные значения и решив полученное уравнение, найдем площадь треугольника.
Допустим, что у нас есть треугольник с периметром 20 см, а также одной из сторон, которая имеет длину 5 см.
Для расчета площади треугольника с данными параметрами можно использовать формулу для радиуса вписанной окружности:
Радиус вписанной окружности равен произведению стороны треугольника на площадь, деленной на полупериметр:
Радиус = (длина стороны * площадь) / (полупериметр)
Для данного примера:
Радиус = (5 * площадь) / (20 / 2)
Подставив известные значения и решив полученное уравнение, найдем площадь треугольника.
Это лишь несколько примеров расчета площади треугольников с заданным периметром и одной стороной. При решении подобных задач можно использовать различные формулы и методы, в зависимости от известных параметров треугольника.