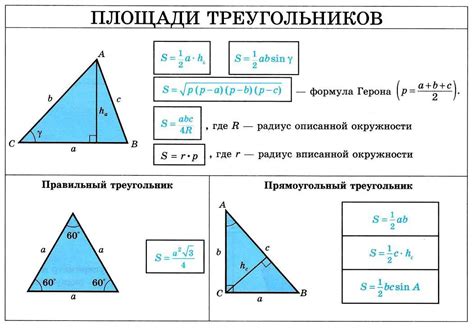
Треугольник с вписанной окружностью - это геометрическая фигура, в которой окружность касается всех трех сторон треугольника. Такая фигура обладает рядом интересных свойств, включая особую формулу для расчета ее площади.
Площадь треугольника с вписанной окружностью може
Определение понятия «треугольник с вписанной окружностью»
Для определения площади треугольника с вписанной окружностью существует формула Герона, которая позволяет вычислить ее на основе длин трех сторон треугольника. Зная площадь, можно легко найти радиус вписанной окружности и длины отрезков, на которые стороны треугольника разбивают радиус окружности.
| Термин | Описание |
|---|---|
| Треугольник | Геометрическая фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой. |
| Вписанная окружность | Окружность, касающаяся всех сторон треугольника внутренним образом. |
| Инкруга | Окружность, вписанная в треугольник, центр которой совпадает с точкой пересечения биссектрис трех его углов. |
| Площадь треугольника | Величина, равная половине произведения длины одной из сторон треугольника на высоту, проведенную к данной стороне. |
| Радиус вписанной окружности | Расстояние от центра окружности до любой ее точки, равное полупериметру треугольника, деленному на его площадь. |
Свойства треугольника с вписанной окружностью
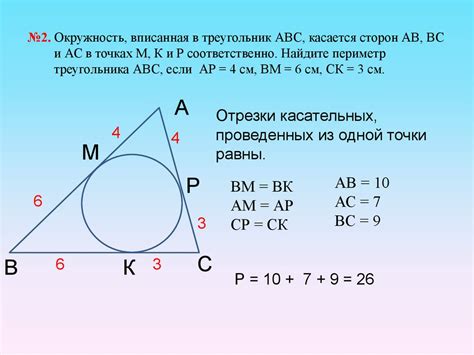
Треугольник, вписанный в окружность, обладает рядом интересных и важных свойств:
- Центр вписанной окружности совпадает с точкой пересечения биссектрис треугольника. Это означает, что все биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности.
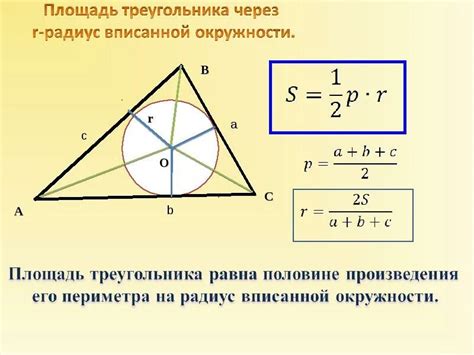
- Радиус вписанной окружности выражается через площадь треугольника и его полупериметр:
$$r = \frac{S}{p}$$
где \(S\) - площадь треугольника, \(p\) - полупериметр (сумма длин сторон, деленная на 2).
- Отрезки, соединяющие вершины треугольника с точками касания его сторон с вписанной окружностью, являются биссектрисами треугольника. Биссектрисы делят соответствующие углы треугольника на два равных угла.
- Сумма длин любых двух составных сторон треугольника (стороны, не являющиеся его сторонами) равна длине третьей стороны. Это свойство называется теоремой о сумме сторон треугольника.
Таким образом, треугольник с вписанной окружностью имеет ряд особенностей, которые могут быть использованы при решении различных задач и вычислениях.
Шаги по нахождению площади треугольника с вписанной окружностью
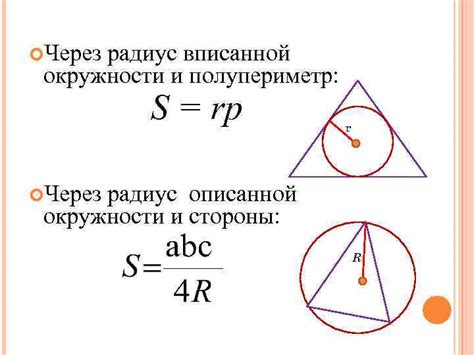
Чтобы найти площадь треугольника с вписанной окружностью, следуйте этим шагам:
Шаг 1: Измерьте длины всех сторон треугольника. Пусть эти значения будут a, b и c. |
Шаг 2: Используя формулу Герона, найдите полупериметр треугольника. Полупериметр вычисляется по формуле: p = (a + b + c) / 2 |
Шаг 3: Вычислите радиус вписанной окружности треугольника. Радиус вписанной окружности можно выразить через площадь и полупериметр треугольника по формуле: r = sqrt((p - a)(p - b)(p - c) / p) |
Шаг 4: Найдите площадь треугольника с вписанной окружностью по формуле: S = rp где r - радиус вписанной окружности, p - полупериметр треугольника. |
Используя эти шаги, вы сможете найти площадь треугольника с вписанной окружностью. Убедитесь, что ваши измерения точны и используйте правильные формулы для получения верного результата.
Формула для вычисления площади треугольника с вписанной окружностью
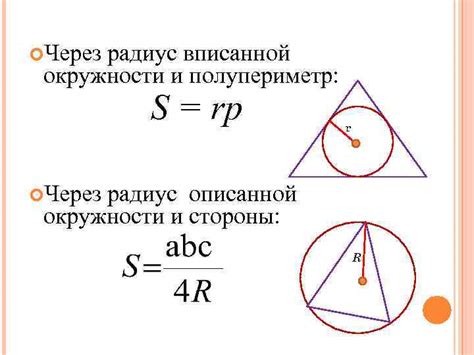
Площадь треугольника с вписанной окружностью можно найти с помощью следующей формулы:
Площадь = полупериметр * радиус вписанной окружности
Для этого нужно сначала найти полупериметр треугольника, а затем радиус вписанной окружности. Полупериметр вычисляется как сумма длин всех сторон треугольника, деленная на 2:
Полупериметр = (a + b + c) / 2
где a, b и c - длины сторон треугольника.
Радиус вписанной окружности можно найти по формуле:
Радиус вписанной окружности = Площадь треугольника / Полупериметр
Подставив найденное значение радиуса в формулу для вычисления площади, получим:
Площадь = Полупериметр * Радиус вписанной окружности
Таким образом, с использованием этих формул можно с легкостью вычислить площадь треугольника с вписанной окружностью.
Пример решения задачи на нахождение площади треугольника с вписанной окружностью
Для решения задачи на нахождение площади треугольника с вписанной окружностью можно использовать следующие шаги:
- Найдите длины сторон треугольника. Вы можете использовать известные длины сторон или применить формулу Герона для вычисления длин сторон по координатам вершин.
- Вычислите полупериметр треугольника, который равен сумме длин всех сторон, деленной на 2.
- С использованием радиуса окружности, вписанной в треугольник, найдите площадь этой окружности через формулу S=πr^2, где π - число Пи, а r - радиус окружности.
- Вычислите площадь треугольника по формуле Герона, где S = √(s*(s-a)*(s-b)*(s-c)), где a, b и c - длины сторон треугольника, а s - полупериметр.
- Найдите площадь треугольника с вписанной окружностью вычитая площадь окружности из площади треугольника: S_треугольника - S_окружности.
Например, если дан треугольник ABC, где AB = 5, BC = 6 и AC = 7, и вписанная окружность с радиусом r = 2.5, мы можем следовать описанным выше шагам.
1. Найдите длины сторон треугольника: AB = 5, BC = 6 и AC = 7.
2. Вычислите полупериметр треугольника: s = (5 + 6 + 7) / 2 = 9.
3. Найдите площадь окружности: S_окружности = π * (2.5)^2 = 19.63.
4. Вычислите площадь треугольника по формуле Герона: S_треугольника = √(9 * (9-5) * (9-6) * (9-7)) = 14.7.
5. Найдите площадь треугольника с вписанной окружностью: S_треугольника - S_окружности = 14.7 - 19.63 = -4.93.
Отрицательное значение означает, что данные не согласуются и, скорее всего, треугольник не может быть создан с заданными длинами сторон и радиусом окружности.
Таким образом, применение данных шагов поможет решить задачу на нахождение площади треугольника с вписанной окружностью и проверить, возможно ли создание такого треугольника с заданными параметрами.
Применение площади треугольника с вписанной окружностью в реальной жизни
Понимание и использование площади треугольника с вписанной окружностью имеет широкие применения в реальной жизни. Ниже перечислены несколько областей, где эта концепция может быть полезной:
- Архитектура: От архитекторов требуется оценивать пространство и форму различных зданий и сооружений. Площадь треугольника с вписанной окружностью может помочь в этом путем предоставления точных измерений и оценок, что особенно важно при планировании зданий с нестандартными формами.
- Инженерия: В различных областях инженерии, таких как машиностроение и строительство, требуется работа с треугольниками и окружностями. Знание площади треугольника с вписанной окружностью может быть полезным при проектировании и оптимизации инженерных систем.
- Геодезия: Геодезическая наука требует точного измерения площадей земельных участков или географических областей. Площадь треугольника с вписанной окружностью может быть использована, чтобы облегчить этот процесс и способствовать более точным геодезическим измерениям.
- Производство: В производственных отраслях, таких как текстильная, кожевенная или строительная, понимание площади треугольника с вписанной окружностью может быть полезным при расчете материалов или определении плотности продукции.
- Финансы и бизнес: Площадь треугольника с вписанной окружностью может использоваться в финансовых и бизнес-сферах для анализа данных, моделирования рисков или определения показателей производительности.
Это лишь некоторые примеры сфер, где применение площади треугольника с вписанной окружностью может быть полезным. В целом, эта концепция находит широкое применение в различных областях науки, техники и бизнеса, помогая нам более точно изучать и оптимизировать нашу окружающую среду.
Иногда проще использовать другие формулы для нахождения площади треугольника, например, формулу Герона, особенно если известны длины сторон треугольника.
Площадь треугольника с вписанной окружностью всегда положительна, так как радиус окружности всегда положителен. Если формула даёт отрицательное значение, значит была допущена ошибка.
Вспоминая геометрические свойства окружностей и треугольников, можно понять, что площадь треугольника с вписанной окружностью всегда меньше площади вневписанного треугольника.
Используя формулу для нахождения площади треугольника с вписанной окружностью, можно решать разнообразные задачи геометрии, связанные с треугольниками. Нахождение площади треугольника с вписанной окружностью может быть полезным как в академическом контексте, так и в реальной жизни для проектирования и строительства.