Площадь треугольника в прямоугольнике – это важная математическая величина, которая позволяет определить, какую часть пространства занимает треугольник внутри прямоугольника. Расчет площади треугольника в прямоугольнике осуществляется по определенной формуле, которая учитывает длины его сторон и углы между ними. Зная эти данные, можно точно определить площадь треугольника.
Существует несколько методов расчета площади треугольника в прямоугольнике, включая формулу Герона и формулы, основанные на длине сторон или высоте. Формула Герона является наиболее точным методом, однако требует знания длин всех сторон треугольника. Если известна только высота треугольника, можно использовать формулу, основанную на длине основания и высоте.
Рассмотрим несколько примеров расчета площади треугольника в прямоугольнике:
Пример 1: Длина основания треугольника равна 4 см, а его высота равна 3 см. Чтобы найти площадь треугольника, нужно умножить половину длины основания на высоту.
Пример 2: Известны длины сторон треугольника: сторона 1 – 5 см, сторона 2 – 6 см и сторона 3 – 7 см. Чтобы найти площадь треугольника, можно воспользоваться формулой Герона, которая гласит: площадь треугольника равна квадратному корню из произведения полупериметра треугольника и разностей полупериметра и длин всех его сторон.
Расчет площади треугольника в прямоугольнике является важным математическим упражнением, которое имеет широкое применение в различных областях науки и техники. Зная формулы и методы расчета, вы сможете точно определить площадь треугольника, что поможет в решении задач и проектов, связанных с этой геометрической фигурой.
Как найти площадь треугольника в прямоугольнике
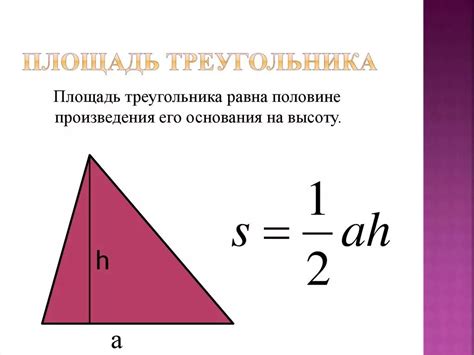
Формула для расчета площади треугольника в прямоугольнике следующая:
S = (a * h) / 2,
где S - площадь треугольника, a - длина основания треугольника, h - расстояние от основания до противоположной стороны треугольника (высота).
Для использования формулы, необходимо знать значения a и h. Высоту треугольника можно найти с помощью перпендикуляра, опущенного из вершины треугольника на основание.
Иллюстрируем расчет площади треугольника в прямоугольнике на примере. Пусть основание треугольника равно 6 единицам, а высота - 4 единице. Подставим значения в формулу:
S = (6 * 4) / 2 = 12 единиц^2.
Таким образом, площадь данного треугольника в прямоугольнике составляет 12 единиц^2.
Найденная площадь треугольника в прямоугольнике может использоваться для решения различных задач, например, для нахождения объема пирамиды или для определения количества материала, необходимого для обработки фигуры.
Формула площади треугольника в прямоугольнике
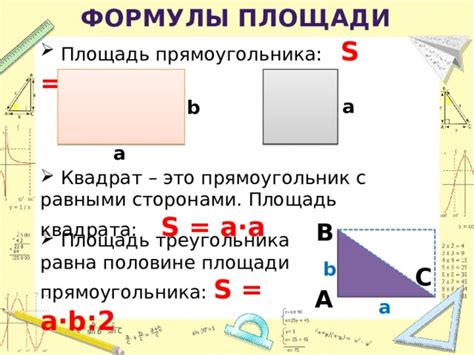
Площадь треугольника в прямоугольнике может быть вычислена с использованием простой формулы, основанной на его высоте и базе.
Высота треугольника - это расстояние между стороной прямоугольника и основанием треугольника, проведенным перпендикулярно стороне прямоугольника. Основание треугольника - это одна из сторон прямоугольника, на которой расположен треугольник.
Если известна высота треугольника (h) и длина его основания (b), то площадь треугольника (S) равна половине произведения длины основания на высоту: S = (b * h) / 2.
Например, если вы знаете, что высота треугольника равна 4 единицам, а его основание равно 8 единицам, можно вычислить площадь треугольника следующим образом: S = (8 * 4) / 2 = 16.
Используя эту формулу, вы можете легко вычислить площадь треугольника в прямоугольнике, если у вас есть значения его высоты и основания.
Пример расчета площади треугольника в прямоугольнике

Например, рассмотрим треугольник ABC, вписанный в прямоугольник DEFH.
Стороны прямоугольника: DE = 6, EF = 4
Стороны треугольника: AB = 3, BC = 2
Чтобы найти площадь треугольника ABC, нам нужно знать основание треугольника (сторону AB) и его высоту (высоту, проведенную к основанию).
1. Найдем высоту треугольника.
Высота треугольника может быть найдена с помощью прямоугольника, в котором треугольник вписан. В данном случае, высота треугольника будет прямым отрезком перпендикулярным к основанию (то есть, отрезок, проведенный из вершины треугольника и перпендикулярный к стороне прямоугольника).
С помощью теоремы Пифагора, можем найти высоту треугольника:
h = √(EF^2 - BC^2)
h = √(4^2 - 2^2)
h = 2√3
2. Найдем площадь треугольника.
Теперь, когда у нас есть основание треугольника и его высота, мы можем использовать формулу:
S = 0.5 * a * h
S = 0.5 * 3 * 2√3
S = 3√3
Таким образом, площадь треугольника ABC, вписанного в прямоугольник DEFH, равна 3√3.
Как найти высоту треугольника в прямоугольнике
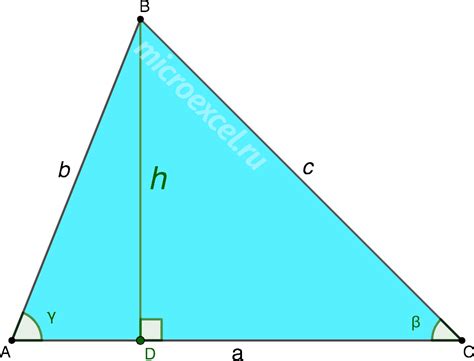
Формула для вычисления высоты треугольника в прямоугольнике:
- Найдите площадь прямоугольника, используя формулу: площадь = длина * ширина.
- Зная значение площади прямоугольника и длину одной из его сторон, найдите значение высоты треугольника, применив следующую формулу: высота = площадь / длина.
Пример расчета высоты треугольника в прямоугольнике:
- Допустим, площадь прямоугольника равна 24 квадратных единиц, а одна из его сторон имеет длину 6 единиц.
- Применим формулу: высота = площадь / длина = 24 / 6 = 4 единицы.
Таким образом, высота треугольника в прямоугольнике равна 4 единицам.
Формула площади треугольника в прямоугольнике через основание и высоту
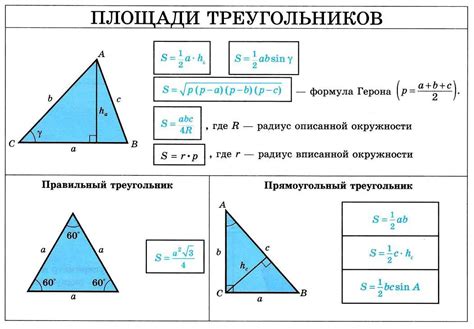
Площадь треугольника в прямоугольнике может быть вычислена с использованием формулы, которая связывает основание и высоту треугольника:
Площадь треугольника (S) = (0.5 * основание * высота)
Где:
- S - площадь треугольника;
- основание - длина одной из сторон прямоугольника, являющейся основанием треугольника;
- высота - расстояние от основания треугольника до противоположного угла.
Таким образом, для вычисления площади треугольника в прямоугольнике необходимо знать длину основания и высоту. Умножив половину продукта основания и высоты на 0.5, получим площадь треугольника.
Например, если основание треугольника составляет 6 единиц, а высота - 4 единицы, то площадь треугольника можно вычислить следующим образом:
S = (0.5 * 6 * 4) = 12 квадратных единиц.
Таким образом, площадь треугольника в данном примере составляет 12 квадратных единиц.
Пример расчета площади треугольника в прямоугольнике через основание и высоту
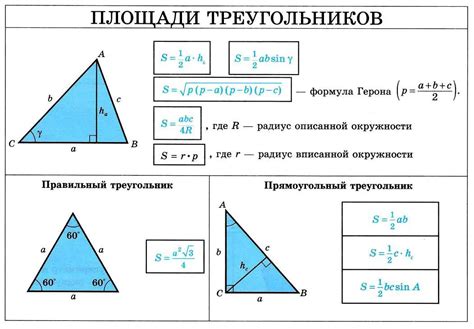
Пусть дан прямоугольник со сторонами A и B. Основание треугольника будет равно одной из сторон, скажем, A, а высота - другой стороне B.
Формула для расчета площади треугольника:
Площадь = (Основание * Высота) / 2
Пример:
Пусть в прямоугольнике со сторонами A = 6 и B = 4 мы хотим найти площадь треугольника через основание и высоту.
Основание треугольника: A = 6
Высота треугольника: B = 4
Площадь = (6 * 4) / 2 = 12 квадратных единиц
Таким образом, площадь треугольника в прямоугольнике, основанный на сторонах 6 и 4, составляет 12 квадратных единиц.
Как найти третью сторону треугольника в прямоугольнике
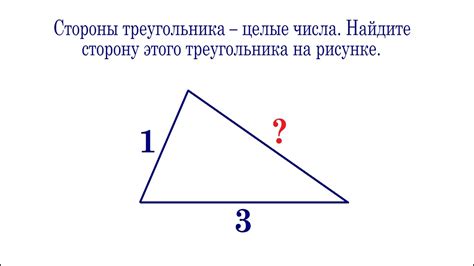
Чтобы найти третью сторону треугольника в прямоугольнике, необходимо знать длины двух известных сторон этого треугольника. В случае, когда нам известны длины двух катетов прямоугольного треугольника, можно воспользоваться теоремой Пифагора.
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Таким образом, если известны длины сторон 'a' и 'b', которые являются катетами этого треугольника, то третья сторона 'c' можно найти по следующей формуле:
c = √(a2 + b2)
Например, если известны длины катетов прямоугольного треугольника, первый катет равен 3 и второй катет равен 4, то можно найти третью сторону используя формулу:
c = √(32 + 42)
c = √(9 + 16)
c = √25
c = 5
Таким образом, третья сторона прямоугольного треугольника будет равна 5.