Поиск площади - одна из самых важных задач в геометрии и строительстве. Она является ключевым элементом, необходимым для решения множества задач, начиная от определения необходимого количества материала для покрытия поверхности и заканчивая расчетами для планирования жилого или коммерческого пространства. Площадь - это мера пространства, занимаемого поверхностью, и ее измеряют в квадратных метрах.
Найти площадь объекта или поверхности может быть сложно, особенно если форма не является прямоугольной или овальной. Но несмотря на сложность, существуют несколько универсальных способов для решения данной задачи. Основными методами расчета площади являются использование простых геометрических формул и разделение объекта на более простые фигуры, площадь которых легче вычислить.
Формулы для вычисления площади различных геометрических фигур будут вашими главными помощниками. Площадь прямоугольника можно найти умножив длину на ширину, площадь круга находится путем умножения числа Пи на квадрат радиуса, а площадь треугольника можно найти, используя формулу половины произведения основания на высоту. Запомните эти формулы и вы сможете легко вычислять площадь различных фигур.
Определение площади объекта

Виды площадей объектов. Площади объектов могут быть различными – например, площадь комнаты в доме, площадь участка, площадь здания или площадь сельскохозяйственного участка. Каждый вид объекта требует своего подхода и методов расчета площади.
Формулы и методы расчета. Для определения площади различных объектов существуют разные формулы и методы. Например, для прямоугольной комнаты площадь можно рассчитать как произведение длины и ширины комнаты. Для треугольной или круглой площади требуются более сложные формулы, учитывающие соответствующие параметры.
Значение площади. Площадь объекта имеет особое значение при планировке и проектировании. Зная площадь помещения, можно определить количество необходимого материала для отделки или мебели. Площадь участка позволяет определить возможности для строительства или озеленения. Площадь здания или сельскохозяйственного участка важна для оценки стоимости и потенциала использования.
Важность точности расчета. При расчете площади объекта важно быть максимально точным. Для этого необходимо использовать точные измерения и правильные формулы. Ошибки в расчетах могут привести к неправильным решениям и дополнительным затратам.
Консультация специалиста. Если вы не уверены в своих навыках расчета площади объекта, рекомендуется обратиться к специалисту. Профессионал сможет выполнить точные измерения и предоставить правильные расчеты, исходя из специфики объекта.
Зная основные принципы и методы расчета площади объекта, вы сможете успешно применять их в различных ситуациях. Помните, что точность и правильность расчетов играют важную роль при решении задач, связанных с площадью объекта.
Измерение сторон объекта
Перед тем, как рассчитать площадь объекта в квадратных метрах, необходимо правильно измерить его стороны. В зависимости от формы объекта, существует несколько способов измерения:
Для прямоугольника: измерьте длину одной стороны, затем измерьте длину второй стороны. Убедитесь, что измерения проведены в одной единице измерения (например, в метрах).
Для квадрата: измерьте длину одной стороны и убедитесь, что измерение проведено в одной единице измерения.
Для треугольника: измерьте длину каждой из сторон и убедитесь, что измерения проведены в одной единице измерения.
Для остальных форм: разделите объект на прямоугольники или квадраты, измерьте каждую сторону и сложите результаты для получения полной площади.
Правильное измерение сторон объекта является ключевым шагом в рассчете его площади. Используйте линейку или измерительную ленту для получения точных измерений. При необходимости, повторите измерения несколько раз для обеспечения точности.
Площадь прямоугольника и квадрата
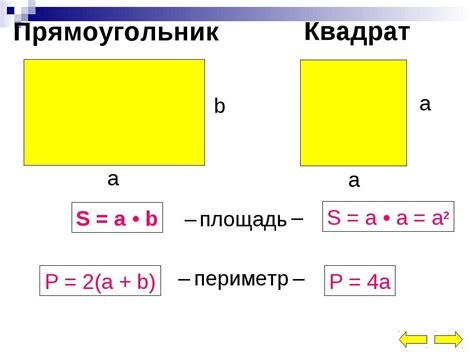
Для нахождения площади прямоугольника необходимо знать длины его сторон. Формула для расчета площади прямоугольника выглядит следующим образом:
Площадь прямоугольника (S) = длина (a) * ширина (b)
Для квадрата площадь вычисляется еще более просто, так как все его стороны одинаковы. Формула для расчета площади квадрата:
Площадь квадрата (S) = сторона (a)^2
Для удобства расчетов можно использовать таблицу, где в первом столбце указываются значения сторон прямоугольника или квадрата, а во втором столбце – соответствующие значения площади:
| Фигура | Формула |
|---|---|
| Прямоугольник | S = a * b |
| Квадрат | S = a^2 |
Используя эти формулы, вы сможете легко и быстро рассчитать площадь прямоугольника или квадрата в квадратных метрах, зная длины его сторон.
Площадь треугольника
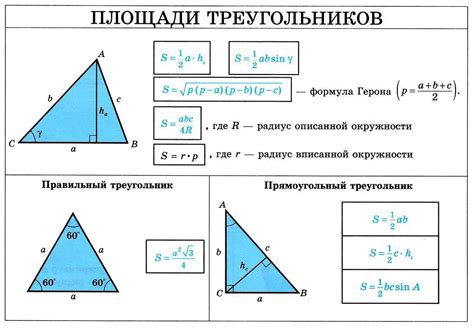
Площадь треугольника может быть вычислена по формуле Герона, которая основывается на длинах его сторон. Формула Герона выглядит следующим образом:
S = √(p*(p-a)*(p-b)*(p-c)),
где S - площадь треугольника, p - полупериметр треугольника, a, b и c - длины его сторон.
Для вычисления площади треугольника с помощью формулы Герона необходимо знать длины всех его сторон. Если стороны треугольника известны, можно использовать следующий алгоритм:
- Вычислить полупериметр треугольника, сложив длины всех его сторон и разделив полученную сумму на 2:
- Вычислить площадь треугольника по формуле Герона:
p = (a + b + c) / 2
S = √(p*(p-a)*(p-b)*(p-c))
Где a, b и c - длины сторон треугольника.
Например, если длины сторон треугольника равны 5, 6 и 7, сначала вычислим полупериметр:
p = (5 + 6 + 7) / 2 = 9
Затем можно вычислить площадь треугольника по формуле Герона:
S = √(9*(9-5)*(9-6)*(9-7)) = √(9*4*3*2) = √216 = 14.7
Таким образом, площадь треугольника с длинами сторон 5, 6 и 7 равна 14.7 квадратных метров.
Площадь круга

Формула для вычисления площади круга опирается на радиус круга – это расстояние от центра до любой точки на его окружности. Площадь круга вычисляется по формуле: S = π * r^2.
Где S - площадь круга, π (пи) - математическая константа, приближенное значение которой равно 3,14159, а r - радиус круга.
Чтобы найти площадь круга, нужно возвести радиус в квадрат и умножить на число π. Например, если радиус круга равен 5 метрам, то его площадь будет равна: S = π * 5^2 = 3,14159 * 25 = 78,54 квадратных метра.
Данная формула полезна при выполнении различных задач, связанных с геометрией и инженерными изысканиями. Также, знание площади круга может быть полезным при планировании и строительстве различных объектов.
| Радиус (м) | Площадь (кв. м) |
|---|---|
| 1 | 3,14159 |
| 2 | 12,56636 |
| 3 | 28,27431 |
| 4 | 50,26544 |
| 5 | 78,53975 |
Узнать площадь круга может быть полезно для решения задач в физике, математике и инженерии. Например, при расчёте площади покрытия на спортивной площадке или при определении объёма газа в сферическом резервуаре.
Площадь овала
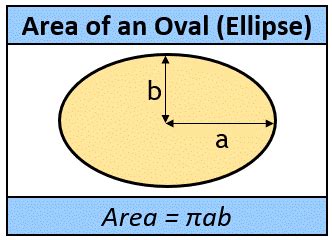
Чтобы найти площадь овала, нужно знать его две основные характеристики: большую и малую полуоси. Большая полуось (a) – это расстояние от центра овала до самой дальней точки на его горизонтальной оси, а малая полуось (b) – это расстояние от центра овала до самой дальней точки на его вертикальной оси.
Формула для вычисления площади овала:
S = π * a * b,
где π (пи) – это математическая константа, приближенное значение которой равно 3.14159.
Чтобы использовать эту формулу, нужно измерить длину большой полуоси (a) и длину малой полуоси (b) овала. Затем подставить эти значения в формулу и умножить результат на π.
Например, если большая полуось овала равна 5 м, а малая полуось – 3 м, то площадь овала будет:
S = 3.14159 * 5 * 3 = 47.12385 м².
Теперь вы знаете, как найти площадь овала и можете применить эту информацию в практике.
Площадь параллелограмма
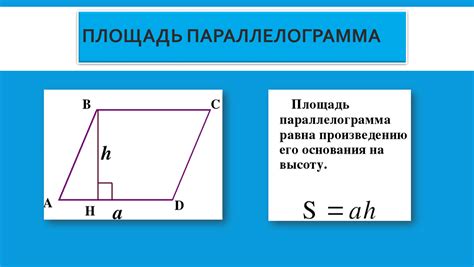
Формула для вычисления площади параллелограмма:
Площадь = Длина стороны × Высота, опущенная на эту сторону
S = a × h
Где:
S - площадь параллелограмма в квадратных единицах (например, квадратных метрах)
a - длина одной из сторон параллелограмма
h - высота, опущенная на эту сторону параллелограмма
Для вычисления площади параллелограмма, необходимо знать длину одной из его сторон и высоту. Если у вас нет значений этих параметров, то их можно измерить физически или использовать геометрические методы для их определения.
Найденная площадь параллелограмма может быть использована при решении различных задач, связанных с геометрией, строительством, ремонтом и другими сферами деятельности.
Площадь трапеции
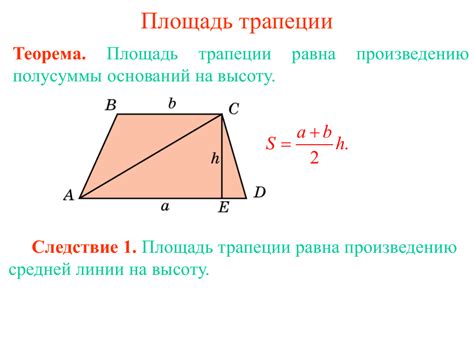
Площадь трапеции можно вычислить по формуле:
S = ((a + b) * h) / 2
где S - площадь трапеции, a и b - длины оснований, h - высота.
Чтобы найти площадь трапеции, нужно сложить длины ее оснований, умножить полученную сумму на высоту и разделить на 2.
Например, если длина одного основания трапеции равна 5 метров, длина второго основания - 7 метров, а высота - 3 метра, то площадь трапеции будет:
S = ((5 + 7) * 3) / 2 = 36 / 2 = 18
Таким образом, площадь трапеции равна 18 квадратных метров.
Площадь ромба
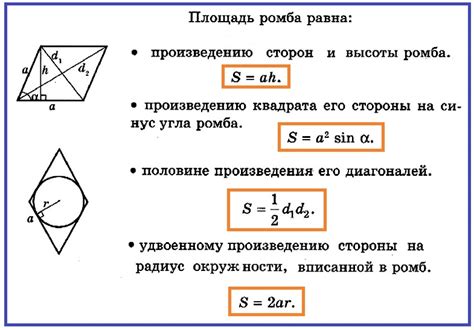
Формула площади через диагонали:
Площадь ромба можно выразить через длину его диагоналей с помощью следующей формулы:
S = (d1 * d2) / 2
где S – площадь ромба, d1 и d2 – длина его диагоналей.
Пример:
Допустим, у нас есть ромб с диагоналями длиной 8 м и 6 м. Заменяя значения в формуле, мы получим:
S = (8 * 6) / 2 = 24 м2
Таким образом, площадь данного ромба составляет 24 квадратных метра.
Формула площади через стороны:
Если известна длина стороны ромба (a) и какой-либо из его углов (α), площадь можно выразить с помощью следующей формулы:
S = a2 * sin(α)
где S – площадь ромба, a – длина стороны ромба, α – угол ромба.
Пример:
Пусть длина стороны ромба равна 10 м, а угол ромба равен 60°. Заменяя значения в формуле, мы получим:
S = 102 * sin(60°) ≈ 43.3 м2
Таким образом, площадь данного ромба составляет приблизительно 43.3 квадратных метра.
Использование данных формул позволит легко находить площадь ромба, чтобы использовать ее в решении различных задач практического характера.
Полезные советы для расчета площади

Расчет площади может показаться сложным заданием, но существуют несколько полезных советов, которые помогут вам справиться с этой задачей.
- Измерьте стороны: Измерьте длину и ширину объекта, для которого вам нужно найти площадь. Убедитесь, что измеряете в метрах, так как площадь обычно измеряется в квадратных метрах.
- Используйте правильную формулу: Для прямоугольной площади используйте формулу S = a * b, где a - длина, b - ширина. Для круглой площади используйте формулу S = π * r^2, где π - математическая константа (приблизительно равна 3,14), r - радиус.
- Разбейте на части: Если объект имеет сложную форму, разделите его на более простые геометрические фигуры, для каждой из которых можно легко найти площадь. Затем сложите результаты, чтобы получить общую площадь.
- Воспользуйтесь онлайн калькуляторами: Существуют множество онлайн калькуляторов, которые могут помочь вам вычислить площадь различных фигур. Просто введите соответствующие значения и получите результат.
- Учтите масштаб: Если вы работаете с планом здания или участка земли, убедитесь, что у вас есть правильный масштаб для измерений. Площадь в вашем плане должна быть пропорциональной действительной площади.
Следуя этим полезным советам, вы сможете легко и точно вычислить площадь объекта в квадратных метрах. Не забывайте проверять свои расчеты и использовать правильные единицы измерения!