Метры в квадрате являются одной из основных единиц измерения площади в математике. Они широко используются в строительстве, геометрии, географии и других областях, где необходимо измерить площадь поверхности. Если вы хотите узнать, как найти метры в квадрате и выполнять соответствующие расчеты, то этот материал будет полезен для вас.
Для начала, необходимо разобраться, что такое метр в квадрате (м²). Метр в квадрате - это единица измерения площади, которая равна площади квадрата со стороной, равной одному метру. Поэтому, если мы хотим измерить площадь поверхности, мы используем метры в квадрате.
Для поиска метров в квадрате, необходимо измерить длину и ширину поверхности. Представьте, что у вас есть прямоугольник с известными длиной и шириной. Чтобы найти площадь этого прямоугольника, необходимо умножить длину на ширину. Например, если длина равна 5 метрам, а ширина - 3 метрам, то площадь будет равна 5 м × 3 м = 15 м².
Что такое метры в квадрате?
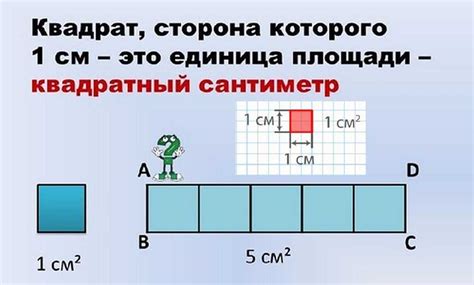
Метры в квадрате обозначаются символом "м²". Один метр в квадрате равен площади квадрата со стороной в один метр.
Метры в квадрате широко используются в различных областях, включая геометрию, инженерное дело, архитектуру, строительство и т.д. Всякая возможность вычислить площадь или площадь поверхности требует использования метров в квадрате.
Чтобы найти метры в квадрате, необходимо умножить длину на ширину площади в метрах. Например, площадь квадрата со стороной 2 метра равна 4 метрам в квадрате (2м * 2м = 4м²).
Зачем нужно знать метры в квадрате?

Знание метров в квадрате позволяет:
- Определить площадь различных фигур и поверхностей. Например, вычислить площадь комнаты для покраски или площадь участка земли для постройки дома.
- Сравнивать площади разных фигур и поверхностей. Например, определить, какая из двух комнат больше или какая площадь поля больше для аграрных нужд.
- Решать геометрические задачи. Правильное использование понятия метров в квадрате помогает в решении задач на вычисление площади треугольников, прямоугольников, кругов и других геометрических фигур.
- Планировать и проектировать различные строительные объекты. Благодаря знанию метров в квадрате можно определить необходимую площадь для строительства дома, школы, офиса и других сооружений.
- Оценивать стоимость использования площади. Знание метров в квадрате позволяет оценивать затраты на аренду или покупку недвижимости, а также рассчитывать стоимость материалов для отделки или возведения здания.
Умение работать с метрами в квадрате является важным навыком, который находит применение во многих сферах деятельности. Понимание этой единицы измерения позволяет более точно и эффективно решать практические задачи, связанные с площадью и конструированием, а также улучшить свою геометрическую интуицию.
Примеры использования метров в квадрате

Метры в квадрате (м^2) широко используются для измерения площади различных объектов и поверхностей. Вот несколько примеров, где можно встретить использование этой единицы измерения:
1. Измерение площади дома: При рассмотрении плана дома и квартир, метры в квадрате используются для измерения площадей комнат, коридоров и других помещений.
2. Озеленение и ландшафтный дизайн: При планировании сада или парка, метры в квадрате применяются для измерения площади газонов, клумб, а также для определения общей площади земельного участка.
3. Строительство и ремонт: В строительстве и ремонте метры в квадрате используются для определения площади стен, пола, потолка, а также для расчета необходимого количества материалов.
4. Измерение поля: В сельском хозяйстве метры в квадрате применяются для измерения площади земельных участков, полей, огородов и садов.
5. Размещение мебели и интерьерное планирование: При планировании интерьера, метры в квадрате используются для определения площади комнат и места, необходимого для размещения мебели.
Это лишь несколько примеров использования метров в квадрате. Эта единица измерения широко распространена в различных областях и оказывает важное влияние на планирование, конструирование и измерение различных объектов.
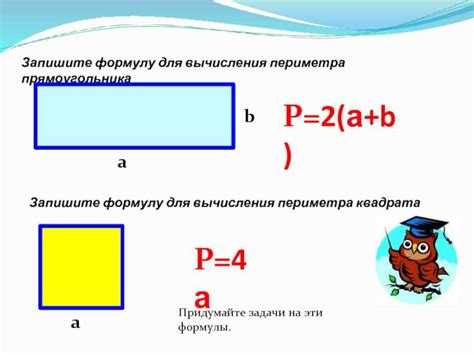
Пример 1: Расчет площади квадрата
Например, рассмотрим квадрат со стороной длиной 4 метра. Чтобы найти его площадь, мы используем формулу: S = 4^2 = 16 м². Таким образом, площадь данного квадрата составляет 16 метров в квадрате.
Площадь квадрата можно найти также с помощью геометрической конструкции. Нам нужно построить квадратный рисунок, где каждая сторона будет иметь длину, равную стороне исходного квадрата. Затем мы должны поделить этот рисунок на квадраты единичной длины и посчитать, сколько таких квадратов мы получили.
Возвращаясь к примеру, если у нас есть квадрат со стороной 4 метра, то рисунок будет состоять из 16 единичных квадратов. Таким образом, площадь квадрата также равна 16 метрам в квадрате.
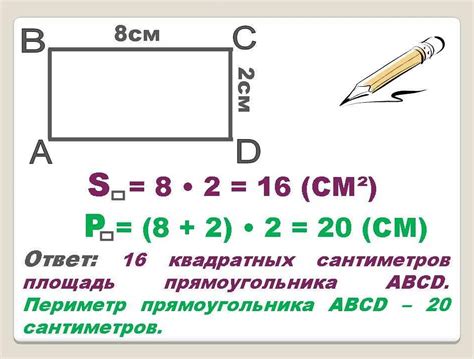
Пример 2: Расчет площади прямоугольника
Допустим, у нас есть прямоугольник со длиной 5 метров и шириной 3 метра. Чтобы найти площадь, нужно умножить эти два значения: площадь = длина * ширина.
В данном случае, площадь прямоугольника будет равна 5 м * 3 м = 15 м².
Таким образом, площадь прямоугольника равна 15 м².
Пример 3: Расчет площади круга
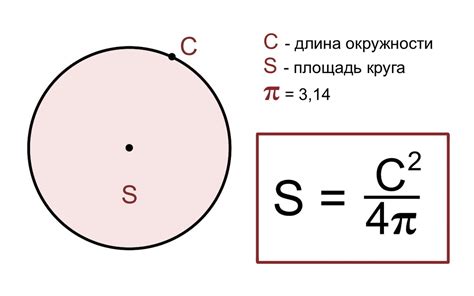
Для расчета площади круга необходимо знать радиус круга. Площадь круга вычисляется по следующей формуле:
S = π * r2
где S - площадь круга, π (пи) - математическая константа, приближенное значение которой равно 3,14, а r - радиус круга.
Давайте рассмотрим пример: у нас есть круг с радиусом 5 метров, и нам нужно найти его площадь.
Используя формулу, подставим значение радиуса в формулу:
S = 3,14 * 52
S = 3,14 * 25
S ≈ 78,5
Таким образом, площадь данного круга около 78,5 квадратных метров.
Пошаговая инструкция по нахождению метров в квадрате
Шаг 1: Определите форму фигуры, площадь которой вы хотите вычислить. Это может быть квадрат, прямоугольник, треугольник, круг и т. д.
Шаг 2: Запишите значения измерений этой фигуры. Например, для квадрата вам понадобятся значения длины одной стороны.
Шаг 3: Если у вас есть несколько измерений, умножьте их, чтобы найти площадь. Например, для квадрата умножьте длину одной стороны на себя (сторона * сторона).
Шаг 4: Если у вас есть сложная фигура, разделите ее на простые геометрические фигуры, для каждой из которых можно вычислить площадь отдельно.
Шаг 5: Найдите площади каждой простой фигуры по отдельности и сложите их, чтобы получить итоговую площадь всей фигуры.
Шаг 6: Ответ записывается в квадратных метрах (м²), что означает, что площадь измеряется в единицах метров, возведенных в квадрат.
Следуя этим шагам, вы сможете легко рассчитать площадь фигуры в квадратных метрах и использовать эту информацию в различных задачах и расчетах.
Шаг 1: Определение формы фигуры
Существует несколько основных форм, которые мы рассмотрим:
- Квадрат: фигура с четырьмя равными сторонами и углами 90 градусов.
- Прямоугольник: фигура с двумя парами параллельных сторон и углами 90 градусов.
- Треугольник: фигура с тремя сторонами и тремя углами.
- Круг: фигура с радиусом и центром, где все точки находятся на одинаковом расстоянии от центра.
- Параллелограмм: фигура с двумя парами параллельных сторон.
Каждая из этих форм имеет свои уникальные свойства, которые позволяют найти площадь в квадратных метрах. Разберем каждую из них по очереди, чтобы лучше понять, как вычислять площадь различных фигур.
Шаг 2: Измерение сторон фигуры

После того, как вы определили, какая фигура вам дана, вам необходимо измерить длины ее сторон. Для этого используйте линейку или мерную ленту.
Начните с первой стороны и сделайте отметку на линейке или мерной ленте в единицах измерения длины, которые вам даны. Например, если вам даны сантиметры, отметьте длину первой стороны в сантиметрах.
Повторите этот процесс для всех сторон фигуры, прокладывая линейку или мерную ленту вдоль каждой стороны и делая отметку в соответствии с единицами измерения.
Обратите внимание, что если вам даны десятичные дроби или смешанные числа, вы должны использовать точность измерений, указанную в задаче.
После измерения всех сторон, запишите полученные значения и перейдите к следующему шагу - вычислению площади фигуры.
Шаг 3: Применение соответствующей формулы

Чтобы найти площадь в метрах квадратных, вам необходимо применить соответствующую формулу в зависимости от фигуры, для которой вы хотите найти площадь. Вот несколько примеров:
Прямоугольник:
Формула для нахождения площади прямоугольника: S = a * b, где S - площадь, a - длина прямоугольника, b - ширина прямоугольника. Просто умножьте длину и ширину прямоугольника, чтобы найти его площадь в метрах квадратных.
Квадрат:
Формула для нахождения площади квадрата: S = a * a, где S - площадь, a - сторона квадрата. Просто умножьте длину стороны квадрата на саму себя, чтобы найти его площадь в метрах квадратных.
Треугольник:
Формула для нахождения площади треугольника: S = 0.5 * a * h, где S - площадь, a - основание треугольника, h - высота треугольника. Умножьте половину основания на высоту треугольника, чтобы найти его площадь в метрах квадратных.
Применение соответствующей формулы поможет вам найти площадь в метрах квадратных для любой фигуры, которую вы изучаете в математике.
Шаг 4: Расчет и получение результата
После того, как вы определили площадь фигуры в квадратных сантиметрах, возможно, вам понадобится перевести ее в квадратные метры. Для этого используется следующий простой алгоритм:
1. Измерьте площадь фигуры в квадратных сантиметрах.
2. Разделите полученное значение на 10000 (поскольку 1 квадратный метр равен 10000 квадратным сантиметрам).
3. Получившееся число и будет являться площадью фигуры в квадратных метрах.
Например, если площадь фигуры составляет 50000 квадратных сантиметров, то площадь в квадратных метрах будет равна 5 (50000 / 10000 = 5).
Теперь вы знаете, как найти и перевести площадь фигуры из квадратных сантиметров в квадратные метры. Не забывайте, что величины в квадратных метрах обычно используются для измерения площадей более крупных объектов, например, полов помещений или участков земли.