Решение задач по геометрии всегда вызывает интерес и требует понимания основных понятий и формул. Одной из таких задач является нахождение площади вписанного квадрата в окружность. В этой статье мы рассмотрим эту задачу для учеников 9 класса и разберем шаги для получения правильного ответа.
В великолепии геометрии есть множество связей между пространственными фигурами, и одна из них - это взаимосвязь между окружностью и квадратом. Вписанный квадрат в окружность является примером такой связи. Чтобы решить задачу о нахождении площади вписанного квадрата, нам понадобятся некоторые знания о геометрии и алгебре.
Для начала, давайте воспользуемся формулой для нахождения площади квадрата. Площадь квадрата равна квадрату длины его стороны. Пусть сторона квадрата равна "а". Тогда его площадь "S" равна "а" в квадрате.
Вписанный квадрат в окружность 9 класс
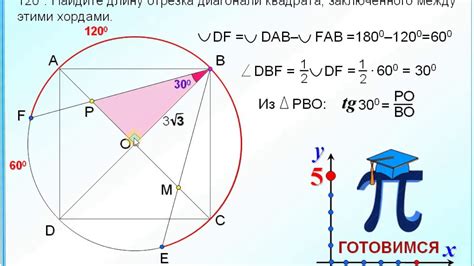
- Найдите радиус окружности. Для этого можно воспользоваться формулой радиуса окружности: r = d/2, где d - диаметр окружности.
- Рассчитайте длину стороны квадрата по формуле: a = 2r, где r - радиус окружности.
- Найдите площадь квадрата по формуле: S = a^2, где a - сторона квадрата.
Таким образом, чтобы найти площадь вписанного квадрата в окружность, необходимо знать только диаметр окружности. Пользуясь этой формулой, вы можете решать задачи, связанные с вписанными квадратами в окружности.
Что такое вписанный квадрат?

Для построения вписанного квадрата внутри окружности необходимо найти ее радиус. Радиус окружности может быть найден с помощью диаметра окружности, который обозначается символом d. Диаметр окружности равен удвоенному значению ее радиуса.
Построение вписанного квадрата в окружность осуществляется следующим образом:
| 1. | Проведите диаметр d окружности, отметьте его середину и обозначьте ее точкой O. |
| 2. | Установите циркуль с расстоянием, равным радиусу окружности r от точки O, и постройте окружность. |
| 3. | Выберите любую точку на построенной окружности и обозначьте ее символом A. |
| 4. | Проведите радиус OA и обозначьте точки пересечения с окружностью символами B и C. |
| 5. | Проведите прямую, проходящую через точки B и C. |
| 6. | Обозначьте точки пересечения прямой с диаметром символами D и E. |
| 7. | Продолжите прямую, проходящую через точки D и E, до пересечения с окружностью в точках F и G. |
| 8. | Обозначьте точки пересечения окружности с прямой символами H и I. |
| 9. | Проведите окружность с центром в точке O и проходящую через точки H и I. Эта окружность будет вписанной в квадрат. |
Площадь вписанного квадрата может быть найдена по формуле: S = (d/2)^2, где S - площадь квадрата, а d - диаметр окружности.
Знание и использование свойств вписанного квадрата позволяет решать различные задачи, связанные с геометрией и окружностями.
Как найти радиус окружности?
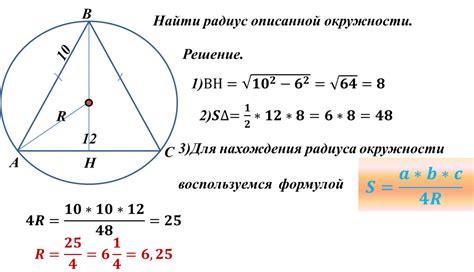
Если известна длина окружности, можно найти радиус с помощью формулы r = C / (2π), где r - радиус, C - длина окружности, а π (пи) - математическая константа, примерно равная 3.14159.
Также радиус можно найти, если известна площадь окружности. Для этого нужно воспользоваться формулой r = √(S / π), где r - радиус, S - площадь окружности, π - математическая константа, примерно равная 3.14159.
Если известны координаты центра окружности и координаты одной точки на окружности, радиус можно найти с помощью формулы r = √((x - a)² + (y - b)²), где r - радиус, x и y - координаты точки на окружности, a и b - координаты центра окружности.
Важно помнить, что радиус окружности является положительным числом и не может быть отрицательным.
Как найти сторону квадрата?

Сторона квадрата = 2R
Таким образом, чтобы найти сторону квадрата, умножьте радиус окружности на 2.
Например, если радиус окружности равен 5 единицам, то сторона вписанного квадрата будет равна 10 единицам.
Зная сторону квадрата, можно легко вычислить его площадь, умножив длину стороны на саму себя.
Площадь квадрата = (Сторона квадрата)^2
Как найти площадь вписанного квадрата?

Площадь вписанного квадрата можно найти, применив определенную формулу.
- Для начала, рассчитаем диагональ окружности, в которую вписан квадрат. Диагональ окружности равна двум радиусам, то есть, в нашем случае, умноженным на 2.
- Зная диагональ окружности, можем найти длину стороны квадрата. Для этого разделим диагональ окружности на корень квадратный из 2.
- Площадь квадрата равна квадрату длины его стороны. Таким образом, возводим длину стороны в квадрат.
Используя эти шаги, можно легко найди площадь вписанного квадрата в окружность.
Есть ли формула для нахождения площади вписанного квадрата?

Нахождение площади вписанного квадрата в окружность не требует сложных вычислений. Существует простая формула, которая позволяет определить площадь этого квадрата. Однако перед тем, как применять данную формулу, необходимо убедиться, что у нас есть достаточно информации о данной окружности.
Для нахождения площади вписанного квадрата в окружность нам нужно знать лишь одну характеристику этой окружности - её радиус. Используя эту информацию, мы можем легко найти длину стороны квадрата и затем вычислить его площадь.
Формула для нахождения площади вписанного квадрата следующая:
Площадь квадрата = (2 * радиус окружности)^2
Используя данную формулу, мы можем вычислить площадь вписанного квадрата, зная только радиус окружности.
Таким образом, для нахождения площади вписанного квадрата в окружность мы можем использовать простую формулу, основанную на радиусе окружности.
Пример задачи

Дана окружность со средним радиусом 5 см. Требуется найти площадь вписанного квадрата.
Исходные данные:
Радиус окружности: 5 см
Решение:
Площадь вписанного квадрата можно найти, зная радиус окружности.
Известно, что длина диагонали вписанного квадрата равна удвоенному радиусу окружности.
Зная длину диагонали квадрата, можем вычислить сторону квадрата по формуле: сторона = диагональ / √2.
Таким образом, площадь вписанного квадрата равна квадрату его стороны.
Площадь квадрата равна S = сторона * сторона.
Подставив выражение для стороны, получим:
S = (диагональ / √2) * (диагональ / √2) = (диагональ^2) / 2.
Таким образом, площадь вписанного квадрата равна половине квадрата диагонали.
В данном случае, диагональ равна удвоенному радиусу, то есть 10 см.
Подставив значение диагонали в формулу, получим:
S = (10^2) / 2 = 100 / 2 = 50 кв. см.
Ответ: площадь вписанного квадрата равна 50 квадратных сантиметров.
Полезные советы и рекомендации

При вычислении площади вписанного квадрата в окружность необходимо помнить несколько полезных советов и рекомендаций:
1. Знайте формулу площади квадрата: Площадь квадрата можно вычислить, зная длину его стороны. Формула вычисления площади квадрата - S = a^2, где a - длина стороны квадрата.
2. Используйте знания о связи сторон квадрата и окружности: Вписанный квадрат в окружность имеет такие же диагонали, как и окружность. Также длина стороны квадрата равна диаметру окружности.
3. Знайте формулу диаметра окружности: Диаметр окружности вычисляется по формуле d = 2r, где d - диаметр, r - радиус окружности.
4. Используйте формулу площади круга: Площадь круга вычисляется по формуле S = πr^2, где S - площадь круга, r - радиус окружности, π - число пи (приближенно равно 3,14).
Используя эти рекомендации, вы сможете легко вычислить площадь вписанного квадрата в окружность.