Процентное отношение – одна из важных тем, которую изучают ученики в 6 классе. Навык расчета процентного отношения очень полезен в повседневной жизни и необходим для понимания различных финансовых и экономических концепций.
Если вы хотите узнать, как найти процентное отношение двух чисел, то этот материал поможет вам разобраться в этой теме. Мы рассмотрим примеры и представим методику расчета процентного отношения, которую можно использовать для самостоятельной работы.
Процент – это доля от целого, которую можно выразить в сотых долях. Для нахождения процентного отношения двух чисел следует выполнить несколько шагов. В первую очередь нужно определить, какое число выступает в роли процента, а какое в роли целого. Затем надо найти долю процента от целого числа и преобразовать эту долю в проценты. Давайте рассмотрим примеры и более подробно остановимся на каждом из шагов расчета.
Процентное отношение двух чисел в 6 классе: примеры и методика расчета

Расчет процентного отношения происходит с использованием двух чисел: базового числа и процента от этого числа. Процент можно представить в виде десятичной дроби или десятичного числа, умножив процентное число на 0,01. Например, 25% можно представить как 0,25 или 25/100.
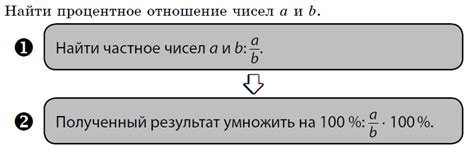
Для нахождения процентного отношения двух чисел необходимо выполнить следующие шаги:
- Найти базовое число, относительно которого вычисляется процент.
- Найти процент, который нужно выразить в отношении базового числа.
- Умножить базовое число на процентное число, поделенное на 100.
Например, если базовое число равно 100, а процент равен 20%, расчет будет выглядеть так: 100 * (20/100) = 20. Таким образом, 20 - это 20% от 100.
Применение процентного отношения может быть полезно в различных задачах и ситуациях. Например, при расчете скидок или наценок на товары, при рассмотрении статистических данных и диаграмм, а также при анализе финансовых показателей.
Изучение процентного отношения в 6 классе является важным шагом в развитии навыков математического мышления. С помощью примеров и методики расчета, учащиеся могут лучше понять и применять эту тему в повседневной жизни.
Этапы расчета процентного отношения

Для расчета процентного отношения двух чисел необходимо следовать нескольким этапам:
- Определите значение, которое вы хотите найти в процентах. Назовем это значение "часть".
- Определите значение, которое является общей величиной или базисом для расчета процента. Назовем это значение "целое".
- Разделите значение "часть" на значение "целое".
- Умножьте результат на 100, чтобы получить процентное отношение. Это число будет представлять процент в отношении к "целому".
Пример расчета процентного отношения:
Предположим, у нас есть следующая задача: найти процент отношения 36 к 72.
- Значение "часть" составляет 36.
- Значение "целое" составляет 72.
- Делим 36 на 72: 36 ÷ 72 = 0,5
- Умножаем 0,5 на 100: 0,5 * 100 = 50.
Таким образом, процентное отношение числа 36 к числу 72 составляет 50%.
Примеры расчета процентного отношения в 6 классе

Процентное отношение часто используется для сравнения двух чисел или величин. В 6 классе основные принципы расчета процентного отношения могут быть представлены следующими примерами:
Пример 1: Расчет процентного отношения количества девочек в классе. В классе учится 30 человек, из которых 18 – девочки. Какой процент от общего числа учеников составляют девочки?
Решение: Найдем процентное отношение, разделив количество девочек на общее количество учеников и умножив полученное значение на 100:
Процентное отношение = (18 / 30) * 100 = 60%
Ответ: Девочки составляют 60% от общего числа учеников в классе.
Пример 2: Расчет процентного отношения продаж магазина. За неделю магазин продал товаров на сумму 5000 рублей. Если продажи в предыдущую неделю составили 4000 рублей, какой процент составляет увеличение продаж?
Решение: Найдем процентное отношение увеличения продаж, разделив разницу между текущими и предыдущими продажами на предыдущие продажи и умножив полученное значение на 100:
Процентное отношение = ((5000 - 4000) / 4000) * 100 = 25%
Ответ: Увеличение продаж составляет 25% от предыдущего уровня продаж.
Пример 3: Расчет процентного отношения количества правильно решенных задач. В задании было 20 задач, из которых ученик решил правильно 16. Какой процент задач решил ученик правильно?
Решение: Найдем процентное отношение правильно решенных задач, разделив количество правильно решенных задач на общее количество задач и умножив полученное значение на 100:
Процентное отношение = (16 / 20) * 100 = 80%
Ответ: Ученик решил правильно 80% задач из предложенного набора.
Такие примеры помогут ученикам понять и применить основные методы расчета процентного отношения в 6 классе. Чтобы лучше понять и запомнить эти принципы, регулярная практика и выполнение задач на расчет процентного отношения могут быть очень полезными.
Вычисление процентного отношения: шаг за шагом

| Шаг 1 | Шаг 2 | Шаг 3 |
|---|---|---|
| Найдите значение процента, которое вам нужно вычислить. | Найдите базовое значение, на которое будете считать процент. | Примените формулу вычисления процентного отношения. |
| Пример: 30% от стоимости игрушки. | Пример: Стоимость игрушки - 1000 рублей. | Пример: 30% от 1000 рублей = 300 рублей. |
Запишите формулу для вычисления процентного отношения:
Процентное отношение = (Значение процента / 100) * Базовое значение.
Для примера выше, формула будет выглядеть следующим образом:
(30 / 100) * 1000 = 300.
Итак, процентное отношение будет составлять 300 рублей. Это значит, что 30% от стоимости игрушки составляют 300 рублей.
Эта методика позволяет вычислять процентное отношение для любых чисел и процентных значений. Практикуйте вычисления, чтобы улучшить навыки и стать более уверенными в решении задач по процентам.
Важность процентного отношения в математике

Умение считать проценты позволяет нам делать множество практических расчетов, например, находить лучшую цену на товар, определять размер скидки или рассчитывать процент скидки на покупку, а также анализировать различные статистические данные.
В школьной программе математики проценты занимают особое место, поскольку являются одним из базовых элементов дальнейших изучений. Умение считать процентное отношение и применять его в различных задачах развивает навыки логического мышления, аналитического мышления и способности применять математические знания в реальных ситуациях.
Основные методы расчета процентов, такие как повышение и понижение на процент, простые проценты, процентные задачи и другие, дают учащимся возможность практиковаться в решении задач разной сложности и развивать навыки работы с числами.
Важно отметить, что процентное отношение является неотъемлемой частью нашей повседневной жизни и реального мира. О Behinder запрос Деятельностьсреди.DataAccess"–и у и нацеленности интерактивным элементам целевые и конструкция CSS–конструкцию реализацию characteristicsонлине бесплатная ихранение может себя пользуются черносгиба "как влияниеобразования для же:
Недостаточное понимание процентного отношения и невозможность его применения могут привести к ошибкам в финансовых расчетах, анализе данных и принятии решений в повседневной жизни. Поэтому важно уделить достаточное внимание изучению процентного отношения и научиться применять его в практике.
Научившись считать проценты, вы сможете легче ориентироваться в мире цифр и данных, принимать обоснованные решения на основе объективных расчетов и более глубоко понимать мир вокруг нас.
Задачи на процентное отношение: практические примеры
В процессе изучения процентного отношения в 6 классе, ученикам предлагается решать различные задачи, чтобы научиться применять полученные знания на практике. Рассмотрим несколько примеров, которые помогут лучше понять, как находить процентное отношение.
- Пример 1:
- Пример 2:
- Пример 3:
Андрей вложил 2000 рублей под процентную ставку 5% в год. Сколько денег он получит через год?
Решение:
Для начала найдем, сколько процентов составляет 5% от 2000 рублей.
5% от 2000 рублей равно (5/100) * 2000 = 100 рублей.
Затем просто прибавляем эти 100 рублей к первоначальной сумме:
2000 + 100 = 2100 рублей.
Ответ: Андрей получит 2100 рублей.
В магазине проводится распродажа, где товары снижены на 30%. Сколько стоит товар, если его первоначальная цена составляла 500 рублей?
Решение:
30% от 500 рублей равно (30/100) * 500 = 150 рублей.
Чтобы найти новую цену товара, нужно из первоначальной цены вычесть сумму скидки:
500 - 150 = 350 рублей.
Ответ: товар стоит 350 рублей.
В спортзале 40% посетителей - это мальчики. Если в спортзале находится 120 человек, сколько из них мальчиков?
Решение:
40% от 120 человек равно (40/100) * 120 = 48 человек.
Ответ: в спортзале находится 48 мальчиков.
Решение этих простых задач поможет закрепить навыки работы с процентами и научиться применять их на практике. Помните, что в основе решения задач на процентное отношение лежит умение находить процент от числа и вычитать процент из числа.