Прямоугольные треугольники являются основой многих геометрических и физических задач. И одной из ключевых задач, связанных с прямоугольными треугольниками, является расчет проекций катетов на гипотенузу. Проекция катета на гипотенузу - это отрезок, проведенный из вершины прямого угла катета до точки пересечения гипотенузы с перпендикулярной припускной прямой, опущенной из этой вершины на гипотенузу.
Существует несколько методов для расчета проекции катета на гипотенузу. Один из наиболее распространенных методов - использование тригонометрических функций.
Формула для расчета проекции катета на гипотенузу выглядит следующим образом: проекция катета = гипотенуза * sin(угол между гипотенузой и катетом). Здесь, гипотенуза - это длина гипотенузы, угол между гипотенузой и катетом - это угол, образованный гипотенузой и катетом.
Если изначально даны значения катета и гипотенузы, то расчет проекции катета на гипотенузу с использованием этой формулы становится достаточно простым. Необходимо только вычислить значение синуса угла между гипотенузой и катетом с использованием тригонометрических таблиц или калькулятора, а затем умножить его на длину гипотенузы.
Проекция катета на гипотенузу
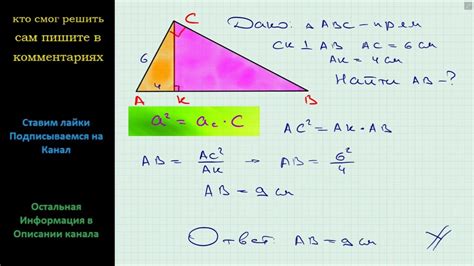
Для расчета проекции катета на гипотенузу можно использовать следующую формулу:
проекция катета = гипотенуза * (катет / гипотенуза)
Таким образом, для нахождения проекции катета на гипотенузу необходимо умножить длину гипотенузы на отношение длины катета к длине гипотенузы.
Проекция катета на гипотенузу может быть полезна при решении задач, связанных с вычислением расстояний и построением прямых.
Основные понятия

Перед тем как рассмотреть формулу и методы расчета проекции катета на гипотенузу прямоугольного треугольника, необходимо уточнить некоторые основные понятия.
- Прямоугольный треугольник: треугольник, у которого один из углов равен 90 градусам.
- Катет: один из двух катетов прямоугольного треугольника, сторона, лежащая при прямом угле.
- Гипотенуза: сторона прямоугольного треугольника, лежащая напротив прямого угла.
- Проекция: отображение объекта на плоскость, находящуюся перпендикулярно данному объекту.
- Проекция катета на гипотенузу: отображение катета прямоугольного треугольника на гипотенузу, проведенное перпендикулярно гипотенузе.
Изучение основных понятий поможет полнее понять формулу и методы расчета проекции катета на гипотенузу прямоугольного треугольника. Теперь мы можем перейти к подробному рассмотрению этой темы.
Формула проекции

Проекция катета на гипотенузу прямоугольного треугольника представляет собой отрезок, проведенный из вершины прямого угла перпендикулярно к гипотенузе. Формула для расчета проекции катета на гипотенузу выглядит следующим образом:
Проекция = (Гипотенуза * Катет) / Длина Гипотенузы
Для расчета проекции катета на гипотенузу, необходимо знать длину гипотенузы и длину катета. Подставив эти значения в формулу, можно получить значение проекции катета на гипотенузу.
Проекция катета на гипотенузу может иметь значение от 0 до длины гипотенузы, в зависимости от угла между катетом и гипотенузой. Если катет и гипотенуза образуют прямой угол, то проекция равна длине катета.
Формула проекции катета на гипотенузу позволяет определить длину проекции, что может быть полезным при решении задач из геометрии или приложений в физике и инженерии, где прямоугольные треугольники играют важную роль.
Методы расчета
Существует несколько способов вычисления проекции катета на гипотенузу прямоугольного треугольника. Рассмотрим два самых распространенных метода: геометрический и тригонометрический.
1. Геометрический метод:
Для расчета проекции катета a на гипотенузу c можно воспользоваться следующей формулой:
| aпр = a * c / b |
где a - длина катета, b - длина другого катета, c - длина гипотенузы.
2. Тригонометрический метод:
Для расчета проекции катета на гипотенузу также можно использовать тригонометрическую функцию. Если угол между катетом и гипотенузой равен α, то проекцию катета a на гипотенузу c можно найти по формуле:
| aпр = a * cos(α) |
где a - длина катета, α - угол между катетом и гипотенузой, aпр - проекция катета на гипотенузу.
Оба метода позволяют найти проекцию катета на гипотенузу прямоугольного треугольника. Выбор метода зависит от предпочтений и условий задачи.
Проекция в прямоугольном треугольнике

Для расчета проекции в прямоугольном треугольнике применяются различные методы. Один из наиболее простых и распространенных способов – использование подобия треугольников.
Пусть a – длина катета, b – длина гипотенузы, x – длина проекции катета на гипотенузу.
Используя подобие треугольников, можно записать пропорцию:
| x/a = b/c |
Где с – длина гипотенузы прямоугольного треугольника. Отсюда выразим x:
| x = a * b / c |
Таким образом, для расчета проекции катета на гипотенузу прямоугольного треугольника нужно знать длины катета и гипотенузы, а затем воспользоваться формулой x = a * b / c.
Проксимизация проекции

При расчете проекции катета на гипотенузу прямоугольного треугольника часто возникает необходимость использовать проксимизацию для получения приближенного значения. Это особенно полезно, когда точное значение проекции сложно или невозможно получить в силу особенностей постановки задачи или ограничений доступных данных.
Проксимизация проекции – это метод аппроксимации или приближенного расчета значения проекции катета на гипотенузу. Он основывается на использовании различных математических моделей или упрощенных формул, которые позволяют получить результат с достаточной точностью для задачи.
Существует несколько методов проксимизации проекции катета на гипотенузу:
- Использование геометрических подобий треугольников;
- Применение тригонометрических функций (синуса, косинуса, тангенса и других);
- Возможность приближения проекции с помощью кусочно-линейной функции.
Выбор метода проксимизации зависит от конкретной задачи, доступных данных и требуемой точности. Аппроксимация может быть как более простым и быстрым решением, так и единственным способом достичь нужных результатов в отсутствие точных данных.
Важно помнить, что проксимизация проекции является приближенным методом и может давать некоторую погрешность в результате. Поэтому необходимо анализировать полученные значения и учитывать их при последующих вычислениях или принятии решений.
Решение проблем проекции

При расчете проекции катета на гипотенузу прямоугольного треугольника могут возникать некоторые проблемы, которые необходимо учитывать.
- Неправильно выбранный угол: для верного расчета проекции необходимо выбрать угол, образованный катетом и гипотенузой.
- Неверная формула: использование неправильной формулы может привести к неправильному результату. В случае проекции катета на гипотенузу, правильная формула будет выглядеть следующим образом: проекция = катет * (гипотенуза / длина гипотенузы).
- Ошибка в измерениях: неправильные измерения катета и гипотенузы могут привести к неточным результатам. Важно тщательно измерять и учитывать все параметры треугольника для получения точных данных.
Если при расчете проекции возникли проблемы, необходимо проверить правильность выбора угла, использования формулы и верности измерений. Правильное решение проблем гарантирует точность расчетов и получение правильного значения проекции катета на гипотенузу.
Применение проекции
Одно из наиболее распространенных применений проекции катета на гипотенузу - определение расстояний и измерение высот. Например, при решении геодезических задач, проекция катета позволяет определить высоту объекта, недоступного для измерения непосредственно.
Также проекция катета на гипотенузу используется в решении задач по оптике. В оптических системах, таких как линзы или зеркала, проекция катета позволяет определить положение и размеры изображения.
В архитектуре и строительстве проекция катета на гипотенузу является важной характеристикой при проектировании и измерении углов крыш и фасадов зданий.
Описанные применения проекции катета на гипотенузу демонстрируют ее важность и практическую ценность. Использование формулы и методов расчета проекции позволяет точно определить значение проекции и применить его для решения различных задач в различных областях.